Exercícios de Lei de Coulomb - Lista de Exercícios Resolvida
Questão 1
Considere um quadrado, com aresta de comprimento , com partículas em todos os seus 4 vértices, conforme mostra a figura.
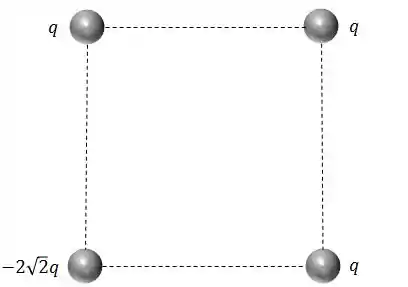
Qual é o módulo da força elétrica resultante sobre a partícula no vértice superior direito?
Ver solução completa
Questão 2
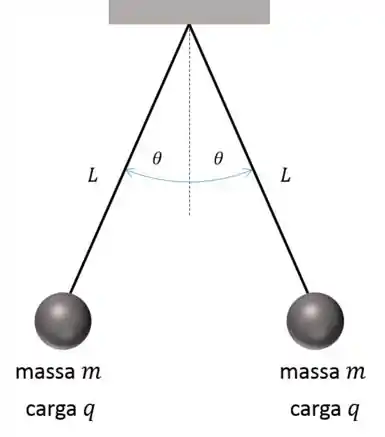
Duas esferas idênticas de massa estão suspensas em fios de seda (??) de comprimento , como indicado na figura abaixo. Cada esfera possui a mesma carga; logo, . O raio de cada esfera é muito pequeno em comparação à distância entre as esferas, de modo que elas podem ser consideradas cargas puntiformes. Mostre que, se o ângulo for pequeno, a distância no equilíbrio entre as esferas será dada por .
Sugestão: quando for pequeno, então
Questão 3
Dada a configuração de cargas abaixo:
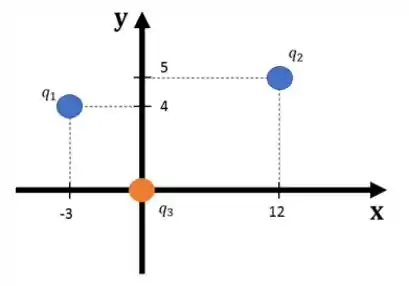
Onde:
Calcule a força resultante sobre a carga .
Ver solução completaQuestão 4
Duas cargas puntiformes e são mantidas fixas a uma distância de . Uma carga , de massa igual a , está inicialmente localizada a de cada uma dessas cargas, como mostra a figura abaixo e é libertada do repouso. Você verifica que a aceleração inicial de é da esquerda para a direita, paralela à linha que liga as duas cargas puntiformes. Dada essa situação, encontre os valores de e .
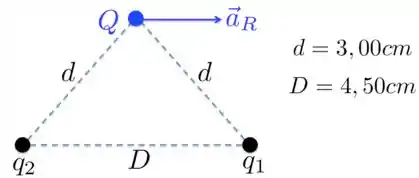
Questão 5
Duas cargas puntiformes positivas estão localizadas sobre o eixo sobre os pontos e . Uma outra carga puntiforme negativa está localizada em algum ponto sobre o eixo .
- Faça um diagrama de corpo livre mostrando as forças que atuam sobre a carga ;
- Encontre as componentes e da força resultante da ação das duas cargas positivas sobre . (Sua resposta deve envolver somente , , , e a coordenada da terceira carga.)
- Qual é a força resultante sobre a carga quando ela está na origem ()?
Questão 6
Dado um sistema isolado conforme discriminado abaixo:
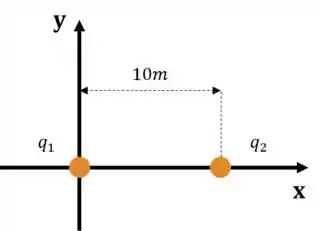
As cargas são dadas por: e .
Calcule o vetor força elétrica que a partícula 1 faz na 2 e o que a partícula 2 faz na 1.
Dado:
Ver solução completaQuestão 7
Uma partícula está rodeada por partículas carregadas situadas em dois anéis concêntricos a ela, conforma mostrado na figura abaixo. Todas as partículas estão fixas em suas posições e suas cargas são indicadas na figura. Os raios dos anéis interno e externo valem e , respectivamente. Utilizando o sistema de coordenadas indicado, qual é a força eletrostática resultante sobre a partícula de carga ?
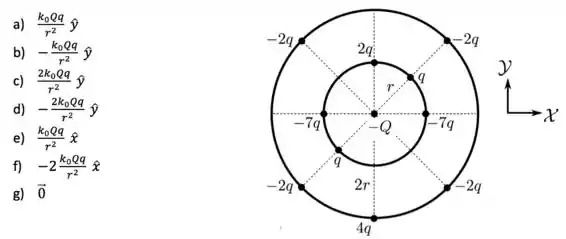
Questão 8
Três cargas puntiformes estão dispostas ao longo do eixo . A carga está na origem e a carga está em . A carga . Onde estará localizado quando a força resultante sobre for no sentido ?
Ver solução completaQuestão 9
(Cap 21 Ex – 3) Qual deve ser a distância entre a carga pontual e a carga pontual para que a força eletrostática entre as duas cargas tenha um módulo de ?
Ver solução completaQuestão 10
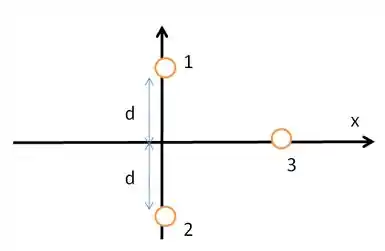
(Cap 21 Ex – 23) Na Fig. 21-31, as partículas e , de carga , estão no eixo , a uma distância da origem. A partícula , de carga , é deslocada ao longo do eixo , de até . Para que valor de o módulo da força eletrostática exercida pelas partículas e sobre a partícula é (a) mínimo e (b) máximo? Qual é o valor (c) mínimo e (d) máximo do módulo?
Questão 11
(Cap 21 Ex – 9) Duas esferas condutoras iguais, mantidas fixas, se atraem mutuamente com uma força eletrostática de quando a distância entre os centros é . As esferas são ligadas por um fio condutor de diâmetro desprezível. Quando o fio é removido, as esferas se repelem com uma força de . Supondo que a carga total das esferas fosse inicialmente positiva, determine: (a) a carga negativa inicial de uma das esferas; (b) a carga positiva inicial da outra esfera.
Ver solução completaQuestão 12
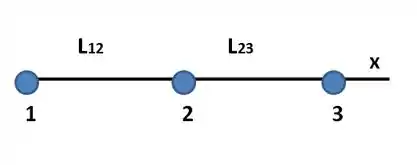
(Cap 21 Ex – 7) Na Fig. 21-22, três partículas carregadas estão em um eixo . As partículas e são mantidas fixas. A partícula está livre para se mover, mas a força eletrostática exercida sobre ela pelas partículas e é zero. Se , qual é o valor da razão ?
Questão 13
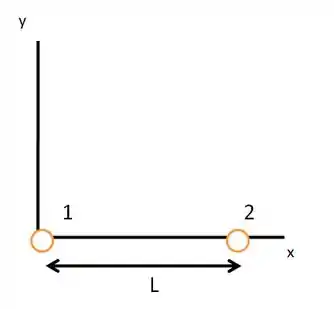
(Cap 21 Ex – 13) Na Fig. 21-25, a partícula , de carga , e a partícula , de carga , são mantidas a uma distância uma da outra, em um eixo . Determine (a) a coordenada e (b) a coordenada de uma partícula de carga desconhecida para que a força total exercida sobre ela pelas partículas e seja nula.
Questão 14
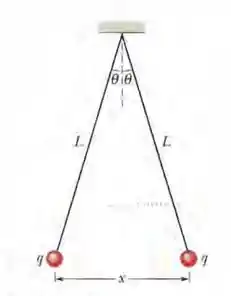
(Cap 21 Ex – 42) Na Fig. 21-38, duas pequenas esferas condutoras de mesma massa e mesma carga estão penduradas em fios não condutores de comprimento . Suponha que o ângulo é tão pequeno que a aproximação pode ser usada. (a) Mostre que a distância de equilíbrio entre as esferas é dada por
(b) Se , e , qual é o valor de |?
Questão 15
(Cap 21 Ex – 22) A Fig. 21-30 mostra um sistema de quatro partículas carregadas,com e . A carga da partícula 2 é ; a carga das partículas e é . (a) Qual deve ser a distância entre a origem e a partícula para que a força que age sobre a partícula seja nula? (b) Se as partículas e são aproximadas do eixo mantendo-se simétricas em relação a esse eixo, o valor da distância é maior, menor ou igual ao do item (a)?
Ver solução completaQuestão 16
(Cap 21 Ex – 1) Da carga que uma pequena esfera contém inicialmente, uma parte é transferida para uma segunda esfera situada nas proximidades. As duas esferas podem ser consideradas cargas pontuais. Para que valor de a força eletrostática entre as duas esferas é máxima?
Ver solução completaQuestão 17
Três partículas pontuais de cargas , e estão localizadas respectivamente nos pontos de coordenadas , e num sistema de eixos cartesianos . Sabendo que , são os vetores unitários nas respectivas direções e , podemos dizer que a forca resultante na partícula de carga devida às outras duas partículas têm a direção e sentido do vetor.
Ver solução completa
Questão 18
Uma partícula está rodeada por partículas carregadas situadas em dois anéis concêntricos a ela, conforma mostrado na figura abaixo. Todas as partículas estão fixas em suas posições e suas cargas são indicadas na figura. Os raios dos anéis interno e externo valem e , respectivamente. Utilizando o sistema de coordenadas indicado, qual é a força eletrostática resultante sobre a partícula de carga ?
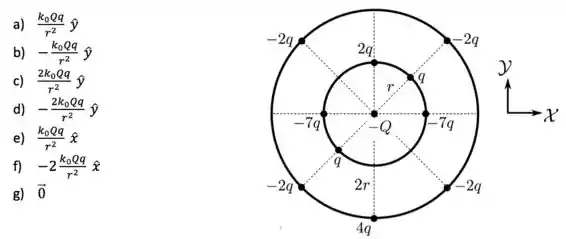
Questão 19
Em um heptágono regular, cuja distância do centro a um dos vértices vale , seis de seus vértices estão ocupados por partículas fixas com a mesma carga , como mostrado na figura abaixo. Utilizando o sistema de eixos da figura, qual é o valor da força eletrostática sobre uma partícula fixa de carga colocada no centro do heptágono?
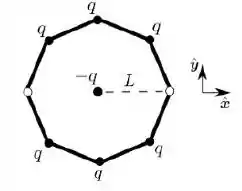
Escolha uma:
Questão 20
A figura mostra um sistema formado por partículas com cargas e e uma das linhas de campo que sai de e chega em . A reta tracejada é perpendicular à reta que passa pelas cargas e estas estão à mesma distância da reta tracejada. A partir do desenho, podemos afirmar que:
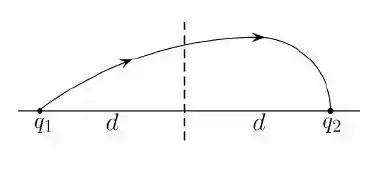
Escolha uma:
Questão 21
Em um heptágono regular, cuja distância do centro a um dos vértices vale , seis de seus vértices estão ocupados por partículas fixas com a mesma carga , como mostrado na figura abaixo. Utilizando o sistema de eixos da figura, qual é o valor da força eletrostática sobre uma partícula fixa de carga colocada no centro do heptágono?
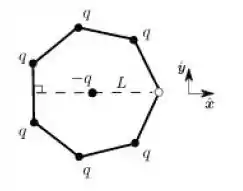
Questão 22
Três partículas carregadas de cargas estão sobre o eixo como mostra a figura. As partículas e são fixas, enquanto que a pode se mover livremente. Sabendo que a partícula está em equilíbrio, qual é o valor da razão ?
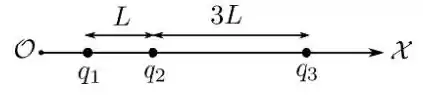 Escolha uma:
Escolha uma:
Questão 23
Quatro cargas de mesmo módulo são dispostas de forma retilínea sobre o eixo de coordenadas , enquanto uma carga de prova positiva encontra-se na origem . Assinale a alternativa para a combinação de sinais das cargas que gera a maior componente positiva x para a força de Coulomb que atua na carga de prova:
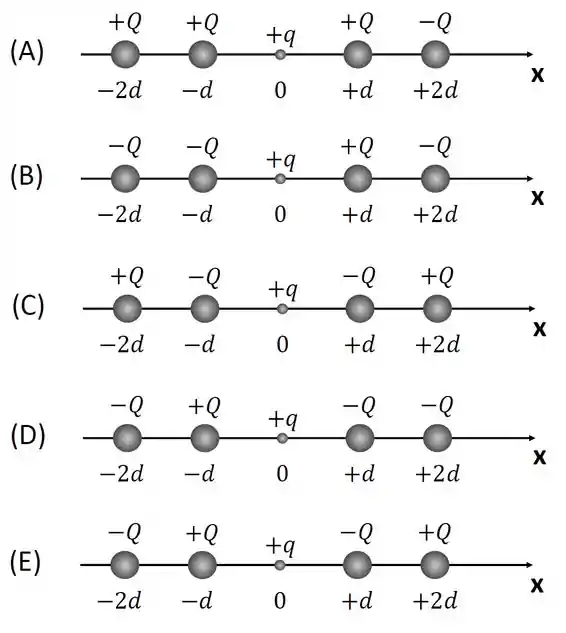
Questão 24
Duas cargas puntiformes, cada uma com carga positiva , estão fixadas a uma distância entre elas. Considere uma terceira carga , também positiva, posicionada em uma altura genérica ao longo da bissetriz do eixo que separa as cargas (veja a figura abaixo) e inicialmente em repouso. A carga só pode se mover ao longo desta bissetriz.
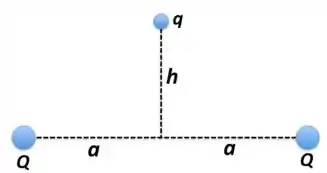
Escolha um sistema de coordenadas apropriado. Em seguida:
- Calcule a força elétrica (módulo, direção e sentido) exercida pelas duas cargas iguais a sobre a carga .
- Encontre a distância para a qual o módulo da força exercida sobre a carga é máximo.
- Calcule o módulo, direção e sentido da força elétrica no item b).
Considere, agora, que a carga da esquerda seja trocada por outra com o sinal negativo, .
d) Calcule, nesta nova condição, as respostas dos itens b) e c).
Ver solução completaQuestão 25
Três partículas de cargas e , e estão localizadas nos pontos de coordenadas , e , respectivamente, num sistema de eixos cartesianos. Sabendo que e são os vetores unitários nas direções e , podemos dizer que a força resultante na partícula de carga devido às outras duas partículas é dada por:
Questão 26
Duas partículas pontuais, cada uma com massa e carga positiva (que chamaremos de partículas ), estão penduradas por fios de comprimento , em equilíbrio estável, como mostra a primeira Figura 1.1 abaixo.
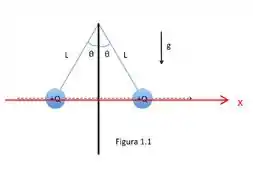
Escolha um sistema de coordenadas apropriado. Em seguida:
- Calcule a força elétrica (módulo, direção e sentido) exercida pelas duas partículas , uma sobre a outra, em função de , e .
- Encontre uma equação para o ângulo de equilíbrio em função de , , e . (Você não precisa resolver essa equação!)
- Calcule o valor da carga .
- Calcule, nesta nova condição de equilíbrio, a que altura abaixo da haste horizontal a nova partícula () vai se situar.
Agora, as mesmas duas partículas do caso anterior estão fixadas nas extremidades de uma haste horizontal de comprimento total , por sua vez presa a uma haste vertical, como mostra a Figura 1.2 abaixo. Uma outra partícula, de carga igual a e de massa , pode deslizar ao longo da haste vertical. Sabendo que, na situação da Figura 1.2, a mesma se encontra em equilíbrio estático, sob a ação de seu peso e das forças eletrostáticas exercidas pelas outras duas partículas.
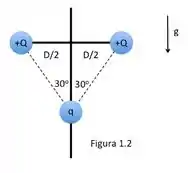
Finalmente, trocamos a partícula de carga e massa por outra de carga e massa . Mais uma vez, a nova partícula atinge o equilíbrio estático, sob a ação de seu peso e das forças eletrostáticas exercidas pelas outras duas partículas.
Questão 27
. Quatro partículas carregadas são fixadas sobre os vértices de um quadrado, como mostrado na figura abaixo. Os valores das cargas são indicados na figura (). Uma quinta partícula de carga é deslocada ao longo do caminho mostrado na figura, partindo do ponto . Esse caminho é constituído de um trecho retilíneo perpendicular ao plano do quadrado e com o ponto coincidindo com seu centro e um trecho retilíneo contido no plano do quadrado e paralelo aos lados horizontais. Sobre essa situação, considere as afirmativas abaixo:
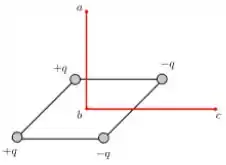
A força elétrica resultante que as quatro partículas fixas exercem sobre é perpendicular à sua trajetória em todos os pontos do caminho .
O trabalho realizado pela força elétrica resultante que as quatro partículas fixas exercem sobre ao longo do deslocamento entre os pontos e é nulo.
O caminho está inteiramente contido em uma superfície equipotencial associada ao potencial resultante das quatro partículas fixas.
É (são) VERDADEIRA(S) a(s) afirmativa(s):
Escolha uma opção:
e
e
e
e
Nenhuma delas
Ver solução completaQuestão 29
Em um experimento, duas esferas de cobre idênticas, carregadas com a mesma carga , são mantidas próximas sem entrarem em contato uma com a outra. Uma das bolas é fixada no teto por meio de um bastão isolante. A outra bola é equilibrada em uma balança, cujo apoio é de plástico isolante. Nesta configuração, a balança registra gramas.
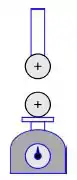
Na sequência, uma esfera idêntica descarregada toca na bola superior e é afastada. Após esse contato, a balança registra . Posteriormente, uma segunda esfera idêntica descarregada toca na bola superior e é afastada. Nesta situação, a balança registra .
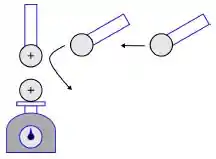
Quais das alternativas abaixo é correta?
Ver solução completa
Questão 30
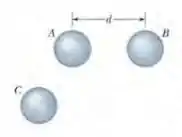
(Cap 21 Ex – 65) As cargas iniciais das três esferas condutoras iguais a da fig. abaixo são as seguintes: esfera A, Q; esfera B, ; esfera C,, em que . As esferas A e B são mantidas fixas, com uma distância entre os centros , que é muito maior que o raio das esferas. A esfera C é colocada em contato primeiro com a esfera A e depois com a esfera B antes de ser removida. Qual é o módulo da força eletrostática entre as esferas A e B?
Questão 31
(Cap 21 Ex – 21) Uma casca esférica não condutora, com um raio interno de e um raio externo de , possui uma distribuição de cargas não uniforme. A densidade volumétrica de carga é a carga por unidade de volume, medida em coulombs por metro cúbico. No caso dessa casca, , em que é a distância em metros a partir do centro da casca e . Qual é a carga total da casca?
Ver solução completaQuestão 32
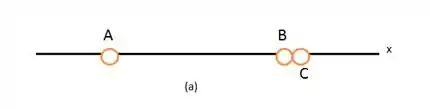
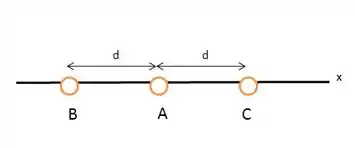
(Cap 21 Ex – 18) Na Fig. 21-28 a, três partículas positivamente carregadas são mantidas fixas em um eixo . As partículas e estão tão próximas que as distâncias entre elas e a partícula podem ser consideradas iguais. A força total a que a partícula está submetida devido à presença das partículas e é N no sentido negativo do eixo . Na Fig. 21-28 b, a partícula foi transferida para o lado oposto de , mas mantida à mesma distância. Nesse caso, a força
total a que a partícula está submetida passa a ser no sentido negativo do eixo x. Qual é o valor da razão ?
(b)
Ver solução completaQuestão 33
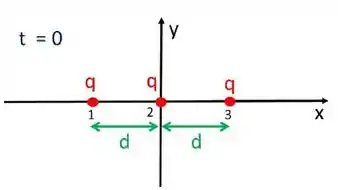
Três partículas idênticas, de massa e carga, se encontram no instante nas posições iniciais , ao longo do eixo , como mostra a Figura. Não considere nenhuma outra força, além das forças eletrostáticas, agindo sobre as partículas.
a) Calcule as forças resultantes sobre cada uma das partículas e, no instante inicial.
b) Calcule a energia eletrostática total no instante inicial.
Após o instante , as partículas são liberadas do repouso para se moverem livremente sob a ação das forças eletrostáticas.
c) Após um tempo muito longo, calcule as posições e velocidades de cada uma das três partículas acima.
Questão 34
A força de Coulomb entre cargas iguais aumenta quando quadruplicamos cada uma das cargas e duplicarmos a distância entre elas.
Verdadeiro ou falso?
Ver solução completaQuestão 35
Duas partículas carregadas são colocadas em pontos fixos com seus centros separados por uma distância de . A carga elétrica dessas partículas vale e . Quanto vale em o módulo da força elétrica entre as cargas? Se necessário use .
Ver solução completaQuestão 36
Q – Uma carga elétrica está em repouso e localizada na posição , sendo . Uma segunda carga elétrica, , de massa , passa pela origem do sistema de coordenadas num instante com velocidade , onde é muito menor do que a velocidade da luz. No instante , o vetor aceleração da carga é:
Ver solução completaQuestão 37
Três cargas puntiformes de igual valor e idênticas massas , são penduradas de um ponto comum por fios isolantes, todos de comprimento . Na situação de equilíbrio, o arranjo fica como ilustrado na Figura ao lado (considere a aceleração da gravidade conhecida).
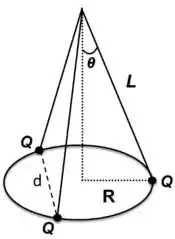
a) Calcule a distância, , de equilíbrio entre as cargas em função de (veja o desenho).
b) Calcule o valor da força elétrica resultante sobre cada uma das cargas devido à ação das demais. Expresse seu resultado em termos do ângulo e do comprimento .
c) Calcule o valor de cada carga em função de , e (Sugestão: lembre-se que no equilíbrio a força total resultante nas cargas deve ser igual a zero).
Ver solução completaQuestão 38
Três cargas são colocadas em três vértices de um quadrado de de lado, como mostrado abaixo.
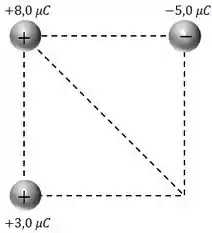
Qual é o módulo aproximado da força eletrostática resultante que uma carga de sentirá se for colocada no quarto vértice?
;
;
;
;
;
Ver solução completaQuestão 39
Considere um eneágono (polígono de nove lados) regular, com partículas de carga em cada um de seus vértices, exceto um deles, conforme mostrado na figura. Qual é a força elétrica resultante sobre uma partícula de carga no centro do polígono.
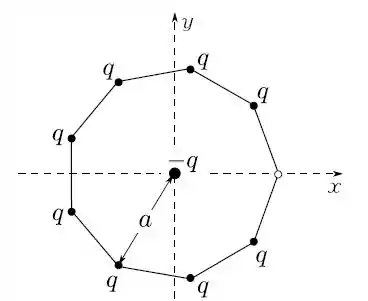
a)
b)
c)
d )
e)
f)
Ver solução completaQuestão 40
Duas cargas elétricas puntiformes iguais estão colocadas a uma distância uma da outra, surgindo entre elas uma força . Se dobrarmos a quantidade de carga elétrica de cada uma delas e reduzirmos a distância à metade, a nova força de interação será
Ver solução completaQuestão 41
Uma bolinha de plástico muito pequena, de massa e carregada com carga , está localizada diretamente acima de uma outra bolinha igual, mas com carga , em um tubo de teste como mostrado na figura.
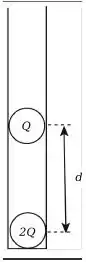
As bolinhas estão em equilíbrio separadas por uma distância . Note que não podemos desprezar a aceleração da gravidade, . Qual é a massa da bolinha?
Ver solução completa
Questão 42
Duas cargas puntiformes encontram-se no vácuo a uma distância de uma da outra. As cargas valem e . Determine a intensidade da força de interação entre elas.
Ver solução completaQuestão 43
Em um laboratório de elétrica, desenvolveu-se o experimento que consistia em colocar duas cargas elétricas positivas de e , em vácuo separadas pela distância de . (Considere )
Ver solução completaQuestão 44
Três partículas de carga são posicionadas sobre um círculo de raio de forma que elas estão equidistantes uma da outra, como mostrado na figura abaixo. Uma quarta partícula de carga é posicionada sobre o centro deste círculo, que coincide com a origem do sistema de coordenadas indicado. Nessa situação, para que a força elétrica resultante sobre qualquer uma das partículas de carga seja nula, o valor de deve ser igual a:
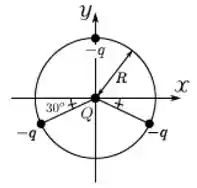
a)
b)
c)
d)
e)
f)
g)
Ver solução completaQuestão 45
5ª questão - Um condutor neutro tem uma cavidade oca dentro dele. Dentro desta cavidade há uma carga de que não toca o condutor. Não há outras cargas nas proximidades. Qual afirmação sobre esse condutor é verdadeira?
A) A superfície interna do condutor carrega uma carga de e sua superfície externa não carrega carga em excesso.
B) A superfície interna e externa do condutor contêm cargas de .
C) O campo elétrico resultante dentro do material do condutor aponta para longe da carga de .
D) A superfície externa do condutor contém de carga e a superfície interna contém .
E) Ambas as superfícies do condutor não carregam excesso de carga porque o condutor está descarregado.
Ver solução completaQuestão 46
Considere um quadrado, com aresta de comprimento , com partículas em todos os seus 4 vértices, conforme mostra a figura.
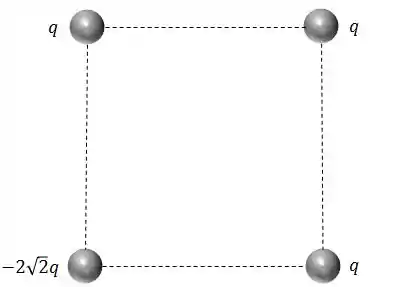
Qual é o módulo da força elétrica resultante sobre a partícula no vértice superior direito?
Ver solução completa
Questão 47
. Três partículas de cargas , e são posicionadas sobre os pontos e do plano de um sistema de coordenadas, respectivamente. Quais valores melhor aproximam as componentes e da força elétrica resultante sobre a partícula de carga , respectivamente?
Dado
Escolha uma opção:
e
e
e
e
e
e
e
e
Ver solução completaQuestão 48
05) Uma esfera condutora maciça de raio '' possui carga . Concêntrica a ela, existe uma casca esférica espessa condutora e descarregada, de raio interno '' e raio externo '', onde . Em certo instante, conectamos a esfera e a casca esférica por um fio condutor, conforme ilustrado na figura. Quando as cargas atingem o equilíbrio:
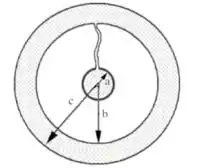
a) A superfície interna da esfera oca tem carga e a esfera maciça tem carga .
b) A superfície externa da esfera oca tem carga e a esfera maciça tem carga .
c) A superfície interna da esfera oca tem carga e a esfera maciça tem carga .
d) A superfície externa da esfera oca tem carga e a esfera maciça tem carga .
e) A superfície externa da esfera oca tem carga e a esfera maciça tem carga .
Ver solução completaQuestão 49
Três cargas , e são colocadas nos vértices de um triângulo equilátero, como mostrado.
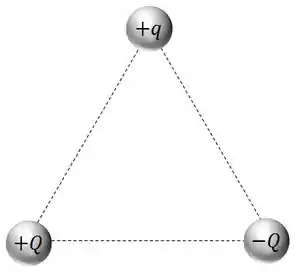
A força resultante sobre a carga devida às outras duas cargas é:
horizontal para a direita;
horizontal para a esquerda;
vertical para baixo;
vertical para cima;
zero;
Ver solução completaQuestão 50
Na figura abaixo, uma pequena esfera de massa e carga é pendurada por um fio fino de massa desprezível. Uma segunda carga é mantida fixa a uma distância de , conforme a figura. Sabendo que é o módulo da aceleração da gravidade, quanto vale ?
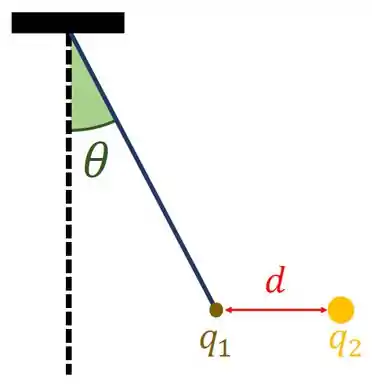
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 51
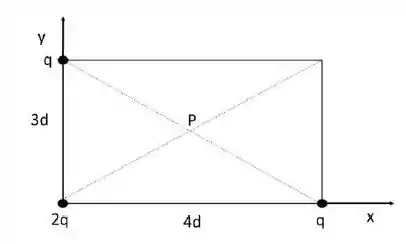
Três cargas, de valores estão colocadas nos vértices de um retângulo de lados e, como mostra a figura.
- Expresse as forças eletrostáticas vetoriais agindo nas partículas localizadas em , e .
- Uma partícula de carga é colocada na posição , que é o centro do retângulo. Calcule o módulo da força eletrostática devida ás três cargas sobre essa partícula.
Questão 52
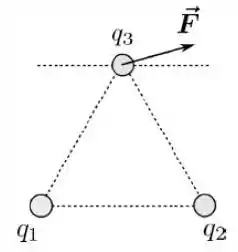
Três partículas carregadas com cargas são fixadas sobre os vértices de um triângulo equilátero. Sabe-se que , enquanto e tem sinais e intensidades a serem determinados. Para isso mede-se a força eletrostática resultante que e exercem em . Notando que a linha tracejada é paralela ao lado horizontal do triângulo, podemos afirmar que:
Escolha uma:
Questão 53
Três partículas de cargas e estão localizadas nos pontos de coordenadas e , respectivamente. Sabendo que são os vetores unitários nas direções e , podemos dizer que a força resultante na partícula devido às outras duas partículas é dada por:
Escolha uma:
Questão 54
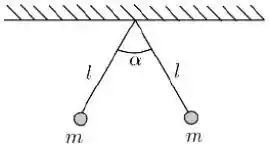
Duas esferas condutoras são suspensas por meio de fios isolantes idênticos e neutros de comprimento . A aceleração da gravidade local tem módulo igual a . Sabendo que as duas esferas possuem a mesma carga e a mesma massa , e que o sistema está em equilíbrio quando o ângulo entre os fios vale , podemos afirmar que satisfaz a relação:
Escolha uma:
Questão 55
(Cap 21 Ex – 19) Na Fig. 21-25, a partícula , de carga , e a partícula , de carga , estão a uma distância uma da outra em um eixo . Se as três partículas permanecem onde estão quando uma partícula 3 de carga é colocada nas proximidades das partículas e, determine (a) a coordenada da partícula : (b) a coordenada da partícula ; (c) a razão .
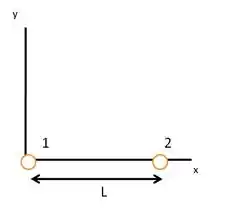
Questão 56
(Cap 21 Ex – 50) A Fig. 21-41 mostra uma barra longa, não condutora, de massa desprezível, de comprimento , articulada no centro e equilibrada por um bloco de peso situado a uma distância da extremidade esquerda. Nas extremidades direita e esquerda da barra existem pequenas esferas condutoras de carga positiva e , respectivamente. A uma distância vertical abaixo das esferas existem esferas fixas de carga positiva . (a) Determine a distância x para que a barra fique equilibrada na horizontal. (b) Qual deve ser o valor de para que a barra não exerça nenhuma força vertical sobre o apoio quando está equilibrada na horizontal?
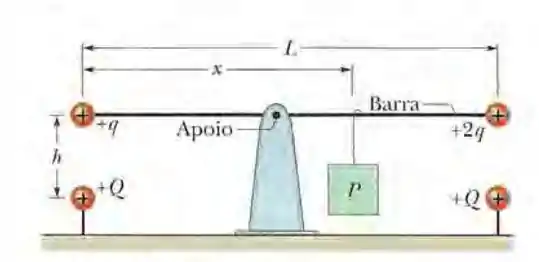
Questão 57
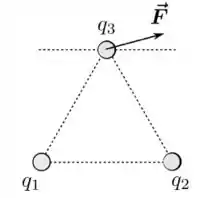
Três partículas carregadas, com cargas , e , são fixadas sobre os vértices de um triângulo equilátero, como mostrado na figura abaixo. Sabe-se que , enquanto e têm sinais e intensidades a serem determinadas. Para isso, mede-se a força eletrostática resultante que e exercem sobre e verifica-se que ela tem a direção e sentido mostrados na figura. Notando que a linha horizontal tracejada na figura é paralela ao lado horizontal do triângulo, podemos afirmar que:
a)
b)
c)
d)
e)
f)
g)
h)
Ver solução completaQuestão 58
Uma partícula de carga está rodeada por partículas carregadas em dois anéis concêntricos a ela, como mostra a figura abaixo. Todas as partículas estão fixas em suas posições e suas cargas são indicadas na figura. Os raios dos anéis internos e externos valem e . Utilizando o sistema de coordenadas indicado, qual é a força eletrostática resultante sobre a partícula de carga ?
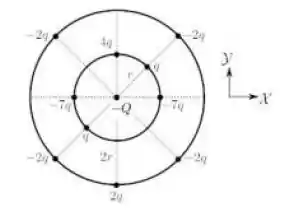
Escolha uma:
Questão 59
Em um octógono regular, cuja distância do centro a um dos vértices vale , cinco de seus vértices estão ocupados por partículas fixas com a mesma carga . O que podemos afirmar sobre as componentes e da força eletrostática que atua sobre uma partícula fixa de carga colocada no centro do heptágono?
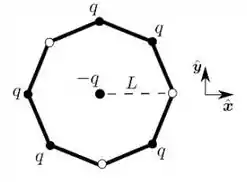
Questão 60
Em um heptágono regular, cuja distância do centro a um dos vértices é , seis de seus vértices estão ocupados por partículas (imóveis) com a mesma carga . Qual é a força eletrostática sobre uma partícula (imóvel) de carga colocada em seu centro?
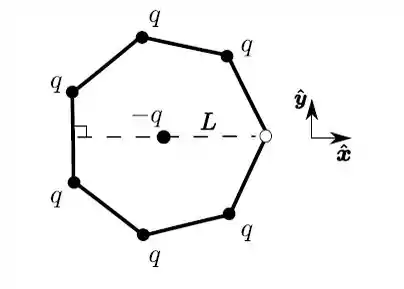
Questão 61
Quando duplicamos a separação entre dois corpos puntiformes eletrizados com cargas iguais, de mesmo sinal, a força entre elas aumenta em quatro vezes.
Verdadeiro ou falso?
Ver solução completaQuestão 62
A figura abaixo mostra quatro cargas pontuais localizadas nos vértices de um quadrado.
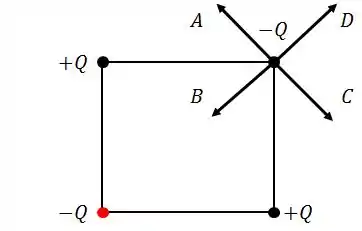
As cargas têm a mesma magnitude e sinais como apresentados na figura. Qual dos vetores (A, B, C ou D) dá a direção e o sentido correto da força resultante sobre a carga que está no canto direito superior?
A
B
C
D
A força resultante nesta carga é nula.
Ver solução completaQuestão 63
1ª questão - Em um octógono regular, cuja distância do centro a um dos vértices é , todos os vértices estão ocupados por cargas imóveis de mesmo módulo e com sinais indicados na figura. Qual é o módulo da força eletrostática sobre uma partícula (imóvel) de carga colocada no centro?
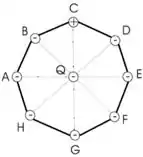
A)
B)
C)
D)
E)
Ver solução completaQuestão 64
(Cap 21 Ex – 44) A que distância devem ser colocados dois prótons para que o módulo da força eletrostática que um exerce sobre o outro seja igual à força gravitacional a que um dos prótons está submetido na superfície terrestre?
Ver solução completaQuestão 65
Uma força de intensidade atua entre duas cargas idênticas que estão separadas por uma distância . Ao dobrarmos a distância de separação das cargas, a intensidade da força eletrostática atuante e a interação entre as cargas será respectivamente:
- e atração
- e repulsão
- Nula e as cargas se mantêm em equilíbrio
- e atração
- e repulsão
Questão 66
Duas cargas de e , estão no vácuo separadas por uma distância . Se dobrarmos a distância entre elas bem como o valor das cargas, a força de repulsão entre elas:
Ver solução completaQuestão 68
Temos três pares de esferas. O par A consiste de duas esferas condutoras, o par B consiste de duas esferas não condutoras e o par C de uma esfera condutora e uma esfera não condutora. Se todas as esferas têm a mesma carga e em cada par as duas esferas estão separadas pela mesma distância, ordene o módulo da força eletrostática entre as duas esferas de cada par quando é positiva nas duas esferas.
Questão 69
Três pequenas esferas, , e têm cargas de mesmo módulo e sinais mostrados abaixo.
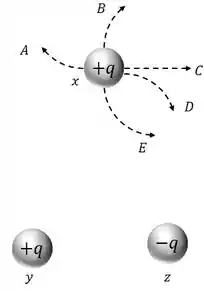
Elas são colocadas nos vértices de um triângulo isósceles, sendo a distância entre e igual à distância entre e . As esferas e são mantidas fixas no lugar, mas a esfera é livre para se mover sobre uma superfície sem atrito.
Que trajetória aproximada ou ) a esfera seguirá após ser solta?
A;
B;
C;
D;
E;
Ver solução completaQuestão 70
No Quadro , duas esferas condutoras idênticas e carregadas, e , possuem a mesma
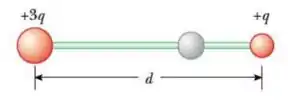
quantidade de carga e têm o mesmo sinal. As esferas são separadas por uma distância ; e a esfera exerce uma força eletrostática sobre a esfera que tem uma magnitude . Uma terceira esfera, , presa a uma haste isolante é introduzida no Quadro . A esfera é idêntica as esferas e , exceto por inicialmente estar carregada com o dobro da carga de . A esfera toca primeiro a esfera , no quadro , e depois toca a esfera , no quadro , e é finalmente removido no Quadro .

Determine a magnitude da força eletrostática que a esfera exerce sobre a esfera no Quadro 4.
Questão 71
Considere duas esferas carregadas respectivamente com e , dispostas horizontalmente e distantes uma da outra. Sendo a constante eletrostática no vácuo igual a , podemos afirmar que a força eletrostática, em Newtons, entre as partículas, vale:
Ver solução completaQuestão 72
Uma partícula condutora eletrizada com carga de é colocada em contato com outra idêntica a ela, porém neutra. Após o contato, as duas partículas ficam carregadas com e são colocadas a uma da outra. Pede-se para determinar o módulo de interação entre elas, sabendo-se que o experimento foi realizado no vácuo.
Dado: constante eletroestática do vácuo
Ver solução completaQuestão 73
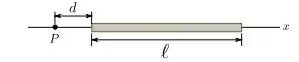
Uma barra de comprimento está sobre o eixo x conforme mostra a Figura 2. Ela possui uma densidade de carga uniforme λ. Determine o campo elétrico no ponto P, situado a uma distância da barra.
Questão 74
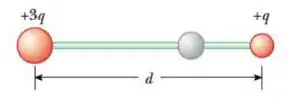
1) Na figura abaixo, as cargas e estão fixas nas extremidades da barra, que é feita de material isolante. A terceira esfera, de cor cinza, pode correr livremente ao longo da barra, e tem carga elétrica não nula, porém desconhecida.
(b) Em caso afirmativo, seria possível conhecer o sinal de sua carga a partir da posição de equilíbrio? Justifique suas respostas.
Questão 75
1) Na figura abaixo, as cargas e estão fixas nas extremidades da barra, que é feita de material isolante. A terceira esfera, de cor cinza, pode correr livremente ao longo da barra, e tem carga elétrica não nula, porém desconhecida.
(a) É possível que a esfera cinza esteja em equilíbrio em algum ponto entre as outras duas cargas?