Linhas de Campo Elétrico
Produzido por Bruno SoaresTeoria
Fala aíi! Bora aprender sobre linhas de campo elétrico com o Responde Aí?!
Vamos ver a relação entre os vetores do campo elétrico e as chamadas linhas de campo elétrico e suas propriedades!
Então bora lá!
Linhas de Força Gerada por Cargas Unitárias
Lembrando que o campo elétrico sai da carga positiva e entra na carga negativa!
Pra você não esquecer é só pensar que a carga positiva cospe o campo elétrico como uma torneira em uma banheira e que a carga negativa puxa o campo elétrico como um ralo em uma banheira!
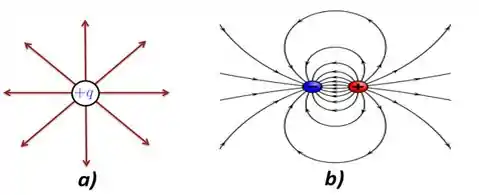
No caso em que temos uma carga positiva ou negativa sozinha, as linhas de força são retas com a mesma direção e sentido dos vetores de campo elétrico. Assim:
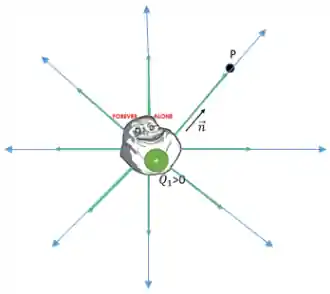
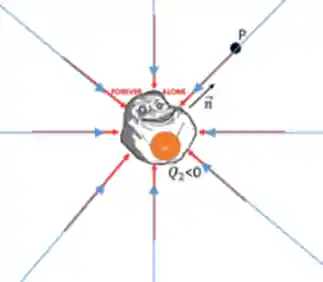
Agora, imagina que temos duas cargas, uma negativa e uma positiva, próximas. Como seriam as linhas de força nas proximidades dessas duas cargas?
Elas seriam assim:
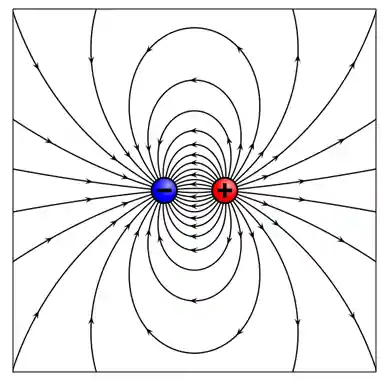
É, eu sei. Muito doido, né? Mas calma que eu vou te explicar porque elas são assim.
Propriedades de Linhas de Força
Primeira Propriedade de Linhas de Força
A primeira coisa que temos que saber sobre essas linhas de força a gente pode observar essa figura aqui:
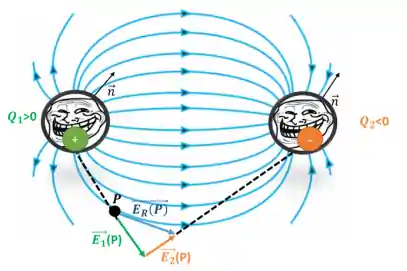
No ponto
Olhando bem esse diagrama, podemos ver claramente que o campo resultante é tangente à linha de força.
Ou seja, a direção da tangente à linha de força no ponto é a mesma que a do vetor campo elétrico resultante.
Isso ocorre para todos os pontos que observarmos sobre uma linha de força, como podemos observar na figura abaixo:
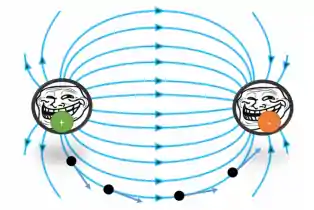
Tem mais: as linhas de força saem da carga positiva e entram na carga negativa, assim como a água sai da torneira e entra num ralo!
Segunda Propriedade de Linhas de Força
Dá uma olhada nessa figura de novo:
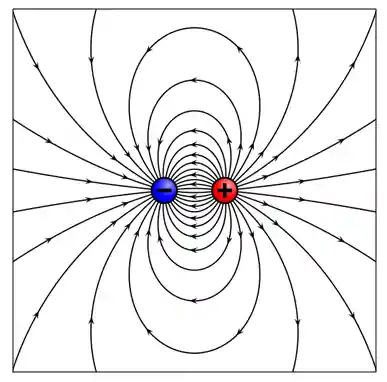
Saca só: linhas mais próximas da carga são mais “coladas”.
Lembra da fórmula do campo elétrico? Quanto menor a distância em relação a carga, maior o campo elétrico. Por isso que desenhamos mais linhas de forças por área quando estamos mais próximos da carga. Essa é a segunda coisa que precisamos saber.
Existe outra coisa que torna o módulo do campo elétrico maior: o valor de
Terceira Propriedade de Linhas de Força
E se as Linhas de força forem geradas por duas cargas de sinais iguais?!
No caso de duas cargas negativas próximas, temos o seguinte:
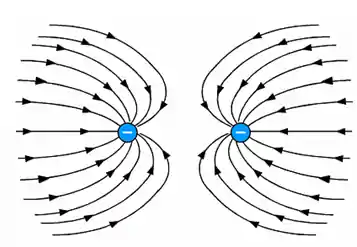
Se tivéssemos duas cargas positivas a figura seria idêntica, só que as setas sairiam das cargas.
Tudo o que concluímos nos casos anteriores vale aqui, mas como o campo elétrico no ponto bem no centro da reta entre as duas cargas é zero, não existe linha de força nesse ponto.
Se as cargas forem diferentes, já sabemos: a carga de maior módulo possui uma maior concentração de linhas de força em sua proximidade.
Isso pode ser visto na figura abaixo:
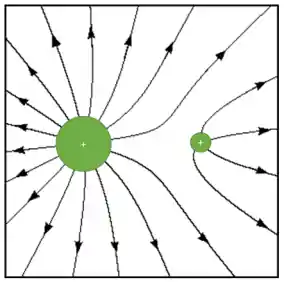
Resumo:
Assim, podemos finalizar este capítulo com um resumo das informações que são cobradas em prova:
- Em um ponto da linha de força, o campo elétrico resultante nesse ponto é tangente à linha de força nesse mesmo ponto. Isso ocorre em duas situações:
- Se estivermos mais próximos de uma das cargas;
- Quando uma carga é maior em módulo do que a outra. Quanto maior o módulo do campo elétrico, mais linhas de força por área nós temos
- Ainda, há dois casos de linhas de força, quando consideramos um par de cargas: o caso de cargas iguais e cargas diferentes. Observe bem as figuras de cada caso que mostramos acima.
- Quando temos cargas de sinais diferentes, as linhas saem da carga positiva e entram na carga negativa;
- Quando temos cargas com o mesmo sinal, as linhas de força de cada carga não irão se tocar.
É isso aí, galera! Agora se liga nesse exercício em vídeo aqui em baixo! 👇
Agora vamos praticar com mais exercícios?!
Propriedades de Linhas de Força
Resumo:
Exercícios Resolvidos
Exercício Resolvido #1
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3 , 8º ed. Rio de Janeiro: LTC , 2008, pp 43-1.
Na figura abaixo, as linhas de campo elétrico do lado esquerdo têm uma separação duas vezes maior que as linhas do lado direito.
(A) Se o módulo do campo elétrico no ponto é , qual é o módulo da força a que é submetido um próton no campo ?
- Dado. Carga elementar:
(B) Qual é o módulo do campo elétrico no ponto ?

Passo 1
O módulo da carga de um próton é igual à carga elementar do elétron. Assim, podemos descobrir a força do próton no campo pela equação da força:
Passo 2
Como a separação das linhas em é duas vezes maior que a separação das linhas no lado direito, a intensidade do campo elétrico na região é a metade da intensidade na região .
Isso porque a cada vez que dobramos a separação de linhas, a intensidade do campo cai pela metade (quanto mais concentradas as linhas, mais intenso é o campo – assim, a separação das linhas é inversamente proporcional ao campo elétrico).
Logo:
Resposta
(a)
(b)
Exercício Resolvido #2
TIPLER, MOSCA, FÍSICA PARA CIENTISTAS E ENGENHEIROS, VOLUME II, 6.ED.
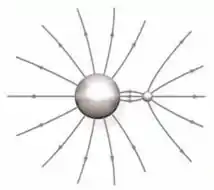
As linhas de campo elétrico para duas esferas condutoras estão mostradas na figura abaixo. Qual é o sinal da carga em cada esfera e quais são as magnitudes relativas das cargas nas esferas?
Passo 1
Para resolver esse exercício, vamos lembrar que a carga na esfera vai ser positiva se tivermos mais linhas SAINDO do que entrando, e vai ser negativa se tiver mais linhas ENTRANDO do que saindo.
Passo 2
Vamos simplesmente contar quantas linhas saem e entram de cada esfera certo? Começando pela esfera maior:
Na esfera maior, tem 11 linhas de campo elétrico saindo enquanto tem 3 entrando, então o número resultante de linhas é
Agora pra esfera menor:
Nela as coisas ficam mais fáceis, temos 8 linhas saindo e nenhuma linha entrando, então o número resultante de linhas vai ser mesmo.
Passo 3
Vamos então determinar o sinal da carga em cada esfera?
Como as duas esferas têm mais linhas saindo do que entrando, as duas estão carregadas positivamente!!!
Agora vamos determinar a magnitude relativa das cargas nas esferas:
Como as duas têm o mesmo número resultante de linhas, as suas cargas são iguais em magnitude ;)
Resposta
As duas esferas estão carregadas positivamente e possuem cargas iguais em magnitude.
Exercício Resolvido #3
UFRJ-P1-2014.2-Múltipla Escolha n°7.
A figura abaixo representa as linhas de campo de duas partículas pontuais com cargas e .
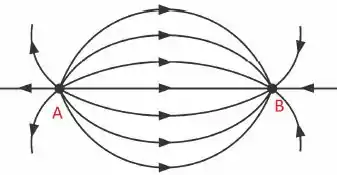
De acordo com essas linhas as cargas e devem ser, respectivamente:
Ambas positivas
Positiva e negativa
Negativa e positiva
Ambas negativas
Positiva e neutra
Neutra e negativa
Passo 1
Aqui basta lembrar que as linhas de campo elétrico saem das cargas positivas, e entram nas cargas negativas.
Assim, se as linhas estão saindo da carga , então ela é positiva. E se as linhas de campo entram na carga , então ela é negativa.
A resposta certa é a .
Resposta
Positiva e negativa
Exercício Resolvido #4
FEI, 1994
Duas cargas puntiformes e estão separadas por uma distância . Assinale a alternativa que melhor represente as linhas de força entre e :
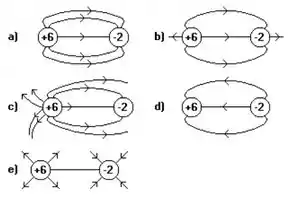
Passo 1
A primeira coisa que a gente deve lembrar é que as linhas de campo vão sempre sair da carga positiva e entrar na carga negativa.
Além disso, como possui módulo maior, vai ter linhas saindo dela mas que não vão entrar em nem em lugar nenhum.
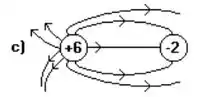
Logo, a única alternativa que satisfaz tudo isso que a gente ta exigindo é a letra C.
Resposta
Exercício Resolvido #5
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 21.59, pp. 35.
Suponha que a carga da Figura a) abaixo seja fixa. Uma pequena partícula com carga positiva é colocada em algum ponto na figura e, a seguir, é libertada.
a) A trajetória da partícula seguirá uma linha de campo elétrico? Por quê?
Suponha, por outro lado, que a partícula seja colocada em algum ponto na Figura b) abaixo e libertada, considerando que as cargas e estão fixas.
b) A trajetória seguirá uma linha de campo elétrico? Novamente, por quê?.
Explique quaisquer diferenças entre suas respostas para as diferentes situações.
Passo 1
Para a gente matar esse exercício, é importante que se lembre de que o campo elétrico é sempre tangente à linha de campo, blz? E o que temos nas figuras acima são extamente as linhas de campo elétrico gerado pelas cargas.
Então, como sabemos que a força sobre uma partícula carregada na presença de é dada por
a força que atua sobre também é tangente às linhas de campo elétrico e, por isso, a partícula carrega vai ter o movimento que tem a mesma direção do campo elétrico , tranquilo?
Passo 2
a) Como temos uma carga , então, no caso da Figura a), a partícula seguirá um caminho cuja trajetória coincidirá com aquela das linhas de campo, como está na figura abaixo.
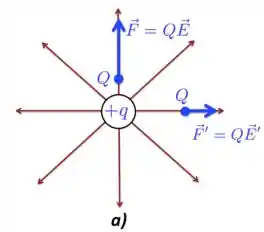
Fica atento, porque, mesmo nesse caso, o campo elétrico também é tangente às linhas de campo em todos os pontos, no entanto, em particular, tem a mesma direção dessas linhas.
Como mostra a figura, as forças e ’ tem intensidades diferentes, pois são tomadas em regiões cujas distâncias da carga são diferentes e, por isso, os campos elétricos e ’. Apesar dos módulos dessas forças serem diferentes, a direção e sentido delas estão ao longo das linhas de campo.
Passo 3
b) Agora, diferente do caso anterior em que a direção de coincidia com as linhas de campo, aqui o campo elétrico continua tangente às linhas de campo, MAS NÃO tem a mesma direção das linhas de campo, como está desenhado abaixo.
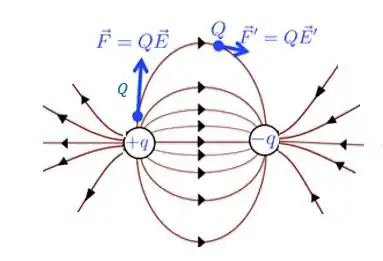
Agora, a força terá a mesma direção que campo elétrico tem no ponto em que estamos considerando. Terá intensidades diferentes ao longo da linha de campo, mas sempre tangente à linha de campo em todos os pontos.
Na figura, seguirá uma trajetória na direção do campo naquele ponto, com forças diferentes em cada ponto, pois o campo também é diferente em pontos diferentes.
Tranquilo? É muito importante que você compreenda a diferença entre esses dois casos, blz?? Fica ligado nisso...
Resposta
- Sim, seguirá a trajetória das linhas de campo, pois a direção de , e portanto a mesma da força , que coincide com a das linhas de campo;
- Não, pois seguirá uma trajetória que é tangente às linhas de campo, já que o campo elétrico é tangente às linhas e, nesse caso, não coincide com as linhas de campo.
Exercício Resolvido #6
UFRJ- Física 3 – P1 2017.1 - DIURNO - 3
A figura mostra um sistema formado por partículas carregadas com cargas e e uma das linhas de campo que sai de e chega em . A reta tracejada é perpendicular à reta que passa pelas cargas e estas estão à mesma distância da reta tracejada.
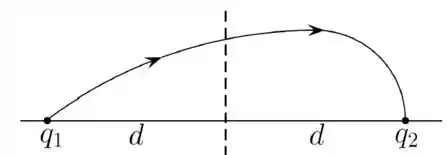
A partir do desenho, podemos afirmar que:
- , e que ;
- , e que ;
- , e seus módulos são iguais;
- , e que ;
- , e que ;
Passo 1
As linhas de campo elétrico saem das cargas positivas e terminam nas cargas negativas. Por isso, a carga é positiva e é negativa neste problema.
Outro ponto importante é: O CAMPO ELÉTRICO EM UM PONTO SOBRE A LINHA DE CAMPO É TANGENTE À LINHA DE CAMPO NAQUELE PONTO. Então, não se confunda: uma linha de campo elétrico não representa, ela mesma, um campo elétrico.
Vamos usar essa informação no próximo passo...
Passo 2
Claramente, cada uma das cargas da figura gera um campo elétrico diferente, pois a intensidade do campo elétrico, tangente à linha de campo, à esquerda da reta tracejada vertical é diferente de sua intensidade à direita desta reta.
Para vermos qual das cargas tem módulo maior, considere a figura abaixo.
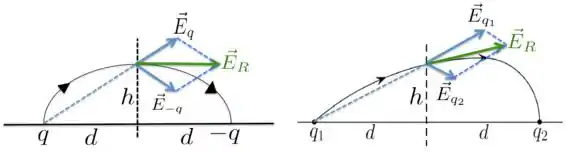
Na figura à esquerda, temos e . Vamos considerar o ponto que está à mesma distância das duas cargas. O campo gerado pela carga positiva é de afastamento e o gerado pela carga negativa de aproximação.
Como as cargas têm mesmo módulo e estão à mesma distância do ponto considerado, os módulos são iguais. Isso significa que o campo resultante é paralelo à linha que une as cargas e , como mostra a figura.
Por outro lado, na figura à direita, o campo elétrico resultante, também tangente à linha de campo nesse mesmo ponto, é diferente daquele da figura à direita. Por isso, o campo elétrico resultante à direita tem intensidade diferente. Até aqui, tá OK?
Agora, repare que o campo resultante à direita está mais inclinado para cima. Isso significa que o campo produzido pela carga é mais intenso e contribui mais para a intensidade do campo resultante, por isso este tem módulo, direção e sentido diferentes como indica a figura.
Portanto, a carga tem módulo maior que a carga : .
Resposta
Portanto, a resposta correta é a letra b)
Exercício Resolvido #7
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 3, 9ª edição. Rio de Janeiro: LTC, 2012, pp 47
Suponha que tenhamos duas cascas esféricas condutoras e concêntricas, onde a de menor raio tem uma carga positiva uniformente distribuída e a de maior raio tem uma carga negativa também uniformente distribuída.
Faça um esboço das linhas de campo elétrico:
I - Entre as duas cascas esféricas
II – Do lado de fora da casca esférica de maior raio
Considere os casos , e .
Passo 1
Primeiramente, devemos observar que os símbolos e usados no enunciado se referem ao valor absoluto das cargas.
Vamos analisar o primeiro caso: .
Temos que a carga na casca interna, é maior que a carga na casca externa, .
Como as linhas de campo elétrico saem das cargas positivas e entram nas negativas, as linhas de campo irão sair da casca interna na direção da casca externa.
Avaliando o campo elétrico do lado de fora da casca externa, o campo resultante será devido à soma das duas cargas. Como , a carga líquida total é positiva ( é negativo).
Portanto, as linhas de campo serão da seguinte maneira:
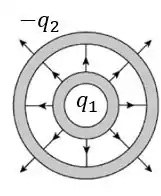
Obs.: podemos reparar que o campo do lado de fora da casca externa é menos intenso do que na parte interna (menos linhas linhas de campo), devido à carga líquida.
Passo 2
Agora vamos analisar o segundo caso: .
As linhas de campo na parte interna, serão iguais às do ítem anterior.
Porém a carga liquida nesse caso será zero.
E, assim, não haverá campo na parte de fora da casca externa.
Portanto, as linhas de campo serão da seguinte maneira:
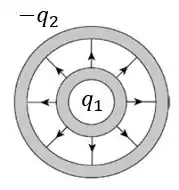
Passo 3
Agora vamos analisar o terceiro e último caso: .
As linhas de campo na parte interna, serão iguais às dos ítens anteriores.
Mas a carga líquida é diferente de zero e haverá um campo na parte de fora da casca externa.
Temos:
Assim, as linhas de campo na parte de fora da casca externa irão entrar na superfície (pois a carga líquida é menor que zero).
Portanto, as linhas de campo serão da seguinte maneira:
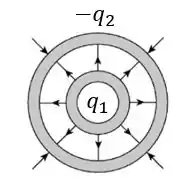
Obs.: podemos reparar que o campo do lado de fora da casca externa é menos intenso do que na parte interna (menos linhas linhas de campo), devido à carga líquida.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #8
UFRJ, Física 3, P1 – 2012.1, Questão ME09
Na figura, temos uma seção tranversal de um corpo condutor, isolado (muito afastado de quaisquer outros corpos), em equilíbrio eletrostático, carregado positivamente, além de algumas curvas orientadas. Qual(is) de tais curvas, nitidamente, não pode(m) representar linhas de campo do correspondente campo eletrostático?
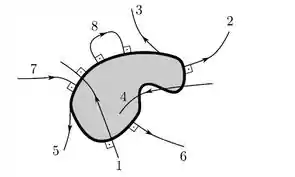
(a) 1 e 4.
(b) 1, 4 e 8.
(c) 2, 6 e 7.
(d) 1, 3, 4, 5, 7 e 8.
(e) 1, 3, 4, 5 e 8.
Passo 1
Esse exercício se torna muito simples se aplicarmos apenas 4 regras. São elas:
1) Linhas de campo saem de objetos carregados positivamente e entram em objetos carregados negativamente.
2) Não pode haver linhas de campo dentro de um material condutor em equilíbrio eletrostático. Pois, se assim fosse, haveria cargas em movimento dentro dele.
3) A linha de campo deve fazer um ângulo de 90º com a superfície do condutor. Caso contrário haveria uma componente tangencial, o que implicaria em ela não ser uma superfície equipotencial (obrigatório no equilíbrio eletrostático).
4) Não podem haver linhas de campo que saem da superfície do condutor e voltam até ela. Caso contrário ela não seria uma superfície equipotencial.
Passo 2
Agora vamos analisar as curvas uma a uma:
A curva 7 desobedece a regra 1, já q o condutor está carregado positivamente.
As curvas 1 e 4 desobedecem a regra 2.
As curvas 3 e 5 desobedecem a regra 3.
A curva 8 desobedece a regra 4.
Passo 3
Portanto, as linhas 1, 3, 4, 5, 7 e 8 não podem representar linhas de campo.
Alternativa correta é a letra (d).
Resposta
(d) 1, 3, 4, 5, 7 e 8.