Soma de Vetores, Subtração e Lei dos Cossenos
Produzido por Ludovic BeghinTeoria
Fala aí, seja muito bem vindo ao Responde Aí! Hoje a gente vai aprender TUDO sobre soma e subtração de vetores! Bora lá? 😉 👇
Adição e Subtração de Vetores pelo Método Geométrico
No método geométrico a gente pega os vetores que estamos interessados em somar e colocamos o inicio de um vetor no final do outro. Assim:
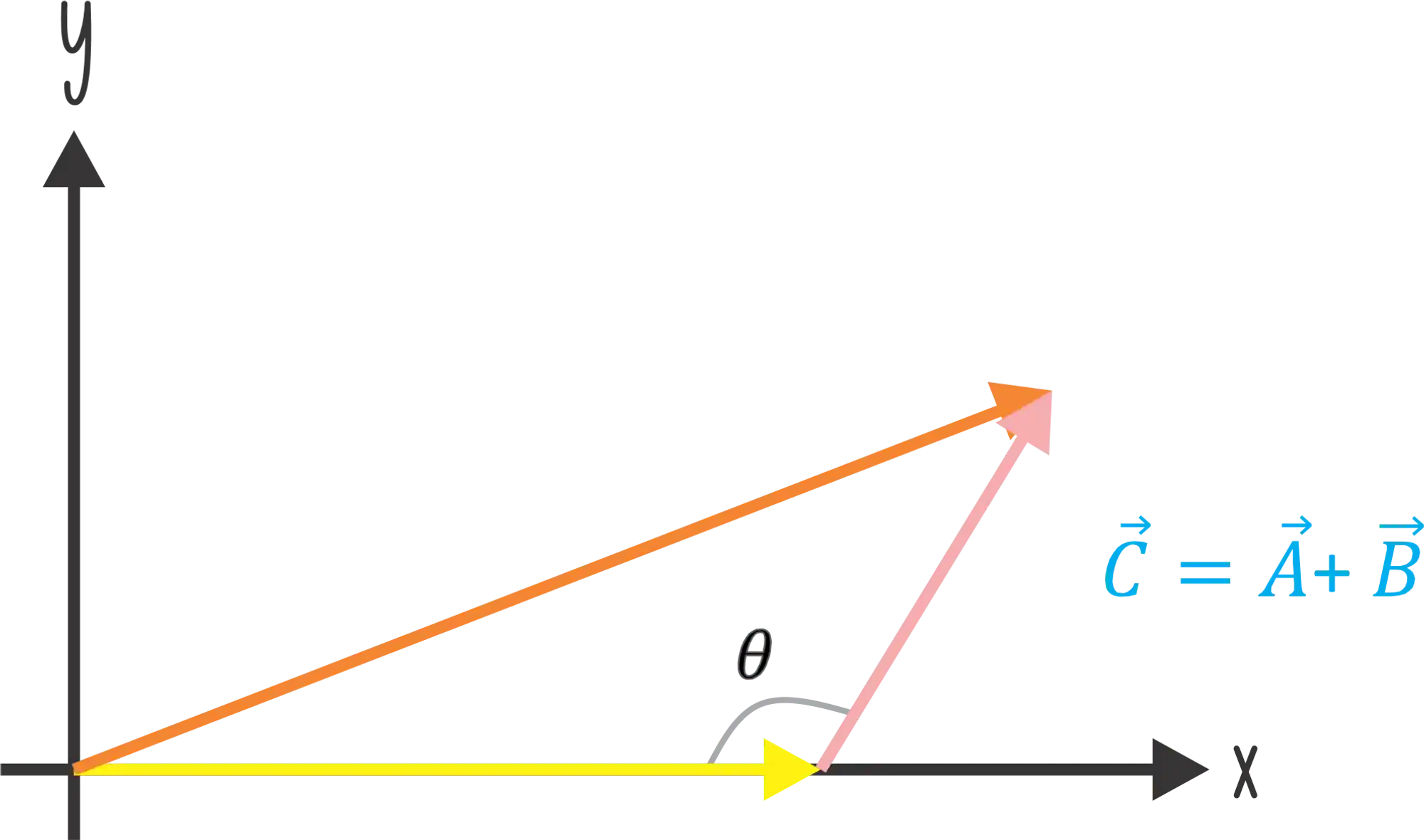
Nesse exemplo acima estamos somando o vetor
📢 Clique para saber mais:
Ahh, outra coisa! Pra subtrair os vetores é a mesma coisa só que nesse caso colocamos o vetor no sentido oposto!
Lei dos Cossenos
-Beleza, mas e agora…como eu faço a soma entre os vetores?! 😖
Percebeu que ali em cima a gente formou um triângulo!? Sabendo o ângulo entre os vetores podemos calcular o tamanho do vetor resultante através da lei dos cossenos:
Onde
Você também pode conferir esse conteúdo em vídeo:
Adição e Subtração de Vetores pelo Método do Paralelogramo
Podemos o método do paralelogramo quando queremos a soma de dois vetores. Diferente do outro método geométrico, colocamos os dois vetores originando do mesmo local. O vetor resultante será a diagonal do paralelogramo formado pelos dois vetores. Assim:
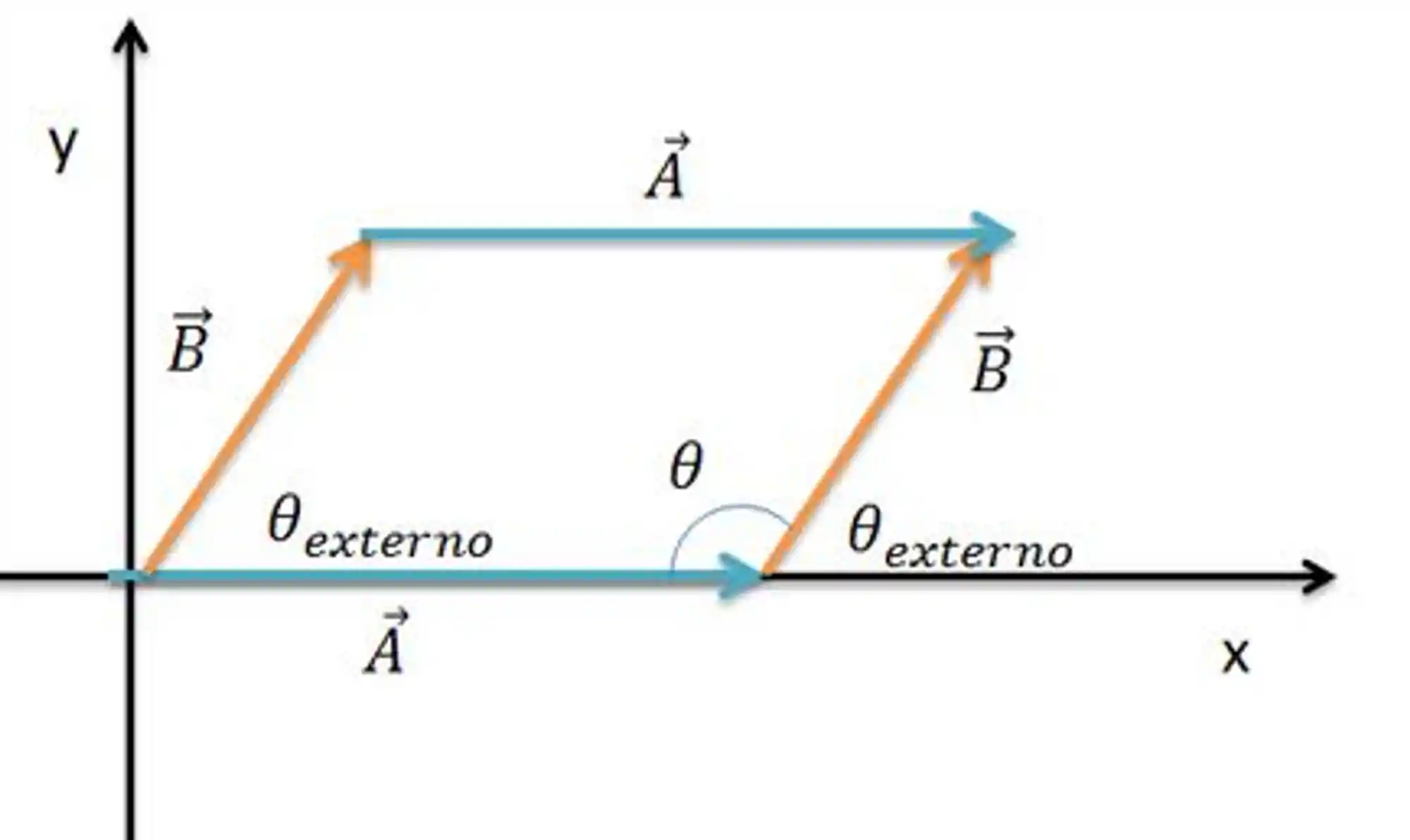
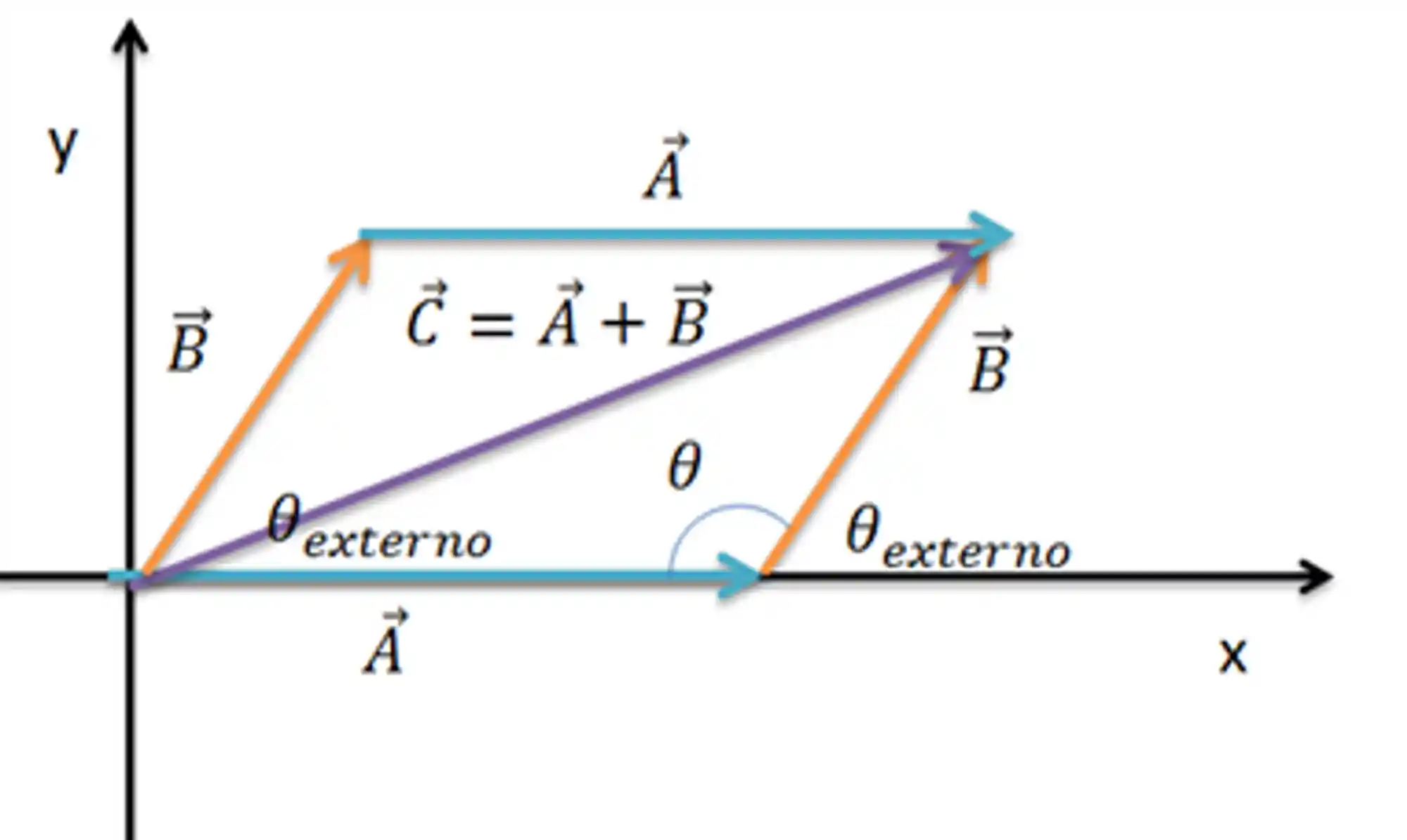
Pra esse caso, vamos usar uma fórmula um pouco diferente que a anterior. O ângulo entre os vetores agora não é o ângulo que forma o triângulo, mas sim o ângulo externo do triângulo. Assim teríamos o seguinte:
Substituindo na lei dos cossenos, temos:
Assim temos:
Propriedades dos Vetores
Além desses métodos, é importante saber algumas propriedades dos vetores:
- Vetores são comutativos: ou seja, não importa você somar o primeiro e depois ou o segundo ou a ordem inversa. O resultado é sempre o mesmo
- A soma vetorial é associativa: não importa qual par seja somado primeiro, o resultado é sempre o mesmo.
- Se dois vetores quando somados resultam em
, significa que um vetor é o negativo do outro
Agora vamos praticar com exercícios?!
Adição e Subtração de Vetores pelo Método do Paralelogramo
Propriedades dos Vetores
Exercícios Resolvidos
Exercício Resolvido #1
TIPLER,P.- Física para Cientistas e Engenheiros, Vol 1,6ª Edição, LTC,2009., pp 24– 52.
Um vetor com unidades de comprimento e um vetor com unidades de comprimento são somados. Sua soma é um vetor com unidades de comprimento.
- Mostre graficamente pelo menos uma maneira pela qual esses vetores podem ser somados.
- Usando seu esboço da parte a), determine o ângulo entre os dois vetores originais.
Passo 1
Essa questão fala sobre a soma de dois vetores, sendo que uma das perguntas é em relação ao ângulo entre eles, certo? Usando essas duas informações, a gente lembra da fórmula da lei dos cossenos.
Passo 2
Alternativa a)
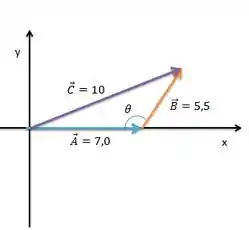
Passo 3
Usando a lei dos cossenos temos:
Resposta
b)
Exercício Resolvido #2
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp. 33 – 1.92.
Quando dois vetores e são desenhados a partir de um mesmo ponto, o ângulo entre eles é .
- Usando técnicas vetoriais, mostre que o módulo da soma destes vetores é dado por
- Se e possuem o mesmo módulo, qual deve ser o valor de para que o módulo da soma de vetores seja igual ao módulo de ou de ?
Passo 1
A gente tem aqui que mostrar que a soma de dois vetores que saiam do mesmo ponto tenham módulo dado pela equação mostrada. Antes de mais nada vamos relembrar o que é o módulo da soma de dois vetores, se liga no desenho:
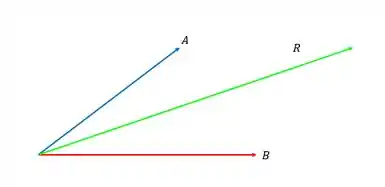
A resultante é a soma dos dois vetores que partem do mesmo ponto, então o seu comprimento é o módulo desse vetor e é ele quem queremos mostrar que é dado pela equação.
Se lembra os modos que a gente aprendeu pra somar dois vetores? Então, essa fórmula ai é muito parecida com a lei dos cossenos, né?
Então elas devem ter algo a ver.

A diferença ta no sinal do ), né? Isso é porque esse ângulo se for comparado ao ângulo que deve ser usado na lei dos cossenos tem o mesmo valor do cosseno só que com o sinal invertido! Se liga só!

Na lei dos cossenos usamos o ângulo , mas podemos usar aplicando a seguinte relação:
Assim, quando eu substituir isso na equação das leis dos cossenos o ultimo termo fica positivo!!!
Passo 2
Letra b) Aqui é o seguinte precisamos encontrar o ângulo entre vetores iguais que façam com que o módulo da soma tenha o mesmo módulo de um dos vetores que são iguais. Então comecemos aqui igualando esses camaradas, já que é o que o enunciado nos fala.
Como ele fala que o módulo resultante da soma é o módulo de ou , podemos substituir na equação.
Assim temos:
Assim temos:
Resposta
Exercício Resolvido #3
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 29 – ex1.30.
Ouvindo o ruído de uma serpente, você faz dois deslocamentos rápidos de e . Usando diagramas (aproximadamente em escala), mostre como esses deslocamentos deveriam ser efetuados para que a resultante tivesse módulo igual a:
Passo 1
Para definir como esses deslocamentos são feitos, vamos usar o ângulo entre os dois vetores e (assumindo que um começa onde o outro termina).
Passo 2
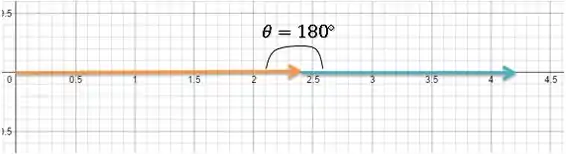
Alternativa a)
Assim:
Passo 3
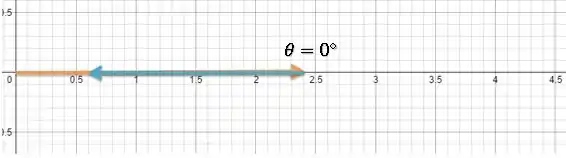
Alternativa b)
Assim:
Passo 4
Alternativa c)
Bom, repara que temos dois ângulos possíveis para .
Tanto o ângulo quanto o ângulo têm cosseno igual a zero:
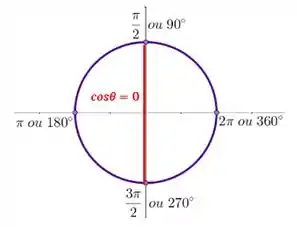
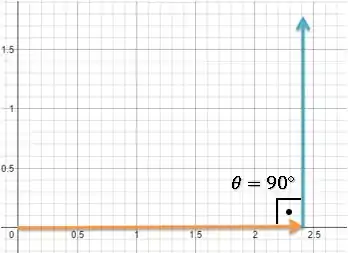
Mas como o enunciado não especifica exatamente a direção dos deslocamentos, dando apenas uma condição de deslocamento resultante, vamos escolher o menor dos ângulos:
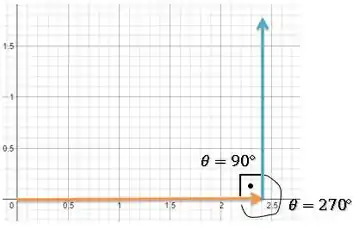
Porém, repara que os ângulos somam (uma volta completa). Portanto, ao escolhermos um dos ângulos, o outro vai aparecer da mesma maneira:
Resposta
a)
b)
c)
Exercício Resolvido #4
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 33 –1.91. Modificado.
Os dois vetores e são desenhados a partir de um mesmo ponto e
- Mostre que quando , o ângulo entre os vetores e é .
- Mostre que quando , o ângulo entre os vetores e é maior do que .
- Mostre que quando , o ângulo entre os vetores e está compreendido entre e .
Considere somente ângulos entre e .
Passo 1
Nessa questão estamos trabalhando com soma de vetores e o ângulo entre eles. Tudo tranquilo até aqui? Se liga nesse desenho aqui que ele vai ajudar a gente a entender o método de soma de veteores que será usado.
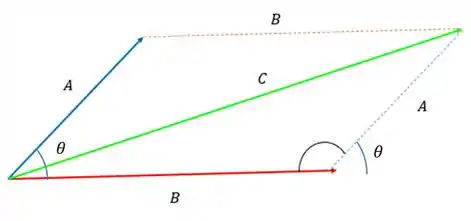
Se lembra que tínhamos dois tipos de soma? A pelo método do paralelogramo e o método geométrico? Aqui vamos usar o método do paralelogramo, pois ele falou que eles partem do mesmo ponto.
E no enunciado foi dado o ângulo entre os vetores , que como podemos ver no desenho acima é o mesmo ângulo externo do paralelogramo que é o ângulo usado na fórmula!
Passo 2
Analisando a equação percebemos que o que está mudando de uma letra pra outra é o ângulo Por isso, vamos analisar o . Pelo círculo trigonométrico sabemos que o cosseno nesse intervalo varia de 1 até -1.
Passo 3
Letra a) Quando temos , temo s o seguinte:
Logo:
Mas como o ângulo precisa estar entre e , teremos:
Passo 4
Letra b)
Quando temos , achamos que:
Se o cosseno do ângulo varia de até 1 mas nesse caso deve ser menor que 0 temos os seguintes limites pro cosseno.
Pelo intervalo analisado só podemos ter valores negativos de cosseno menores que 0. Essa variação de cosseno pode ser visualizada melhor usando o circulo trigonométrico.
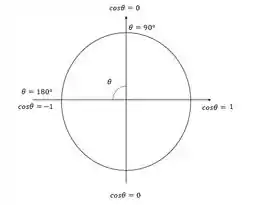
Através do círculo podemos ver que o cosseno tem valor quando for e vale quando for , e dentro desse intervalo é negativo.
Logo, provamos que
Passo 5
Letra c)
Quando temos , achamos que:
Analisando novamente o círculo podemos ver que o cosseno é positivo no intervalo dado:
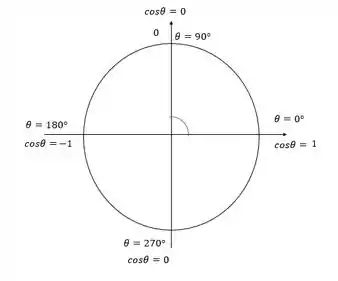
Aonde vemos o cosseno do ângulo vale para e para , sendo positivo nesse intervalo:
Resposta
Ei, a resposta está no passo a passo :)