Exercícios de Componentes de Vetores e Vetores Unitários - Lista de Exercícios Resolvida
Questão 1
Você pode achar uma grandeza vetorial que possua módulo igual a zero, tendo, porém, componentes diferentes de zero? Explique. É possível o módulo de um vetor ser menor que o módulo de qualquer de seus componentes? Explique
Ver solução completaQuestão 2
Em um vôo de treinamento, uma aprendiz de piloto voa de Lincoln, no Estado de Nebraska, até Clarinda, no Iowa; a seguir até St. Joseph, no Missouri: depois até Manhattan, no Kansas, como na figurinha abaixo. Os ângulos formados pelos deslocamentos são medidos em relação ao norte: significa sentido sul para o norte, é o leste, é o sul e é o oeste. Use o método dos componentes para achar:
- A distância que ela terá de voar para voltar para Lincoln
- A direção (em relação ao norte) que ela deverá voar para voltar ao ponto de partida. Ilustre a solução fazendo um diagrama vetorial.

Questão 3
Você deseja programar o movimento do braço de um robô em uma linha de montagem para se mover no plano . Seu primeiro deslocamento é ; seu segundo deslocamento é , cujo módulo é igual a , formando um ângulo de , medido considerando-se uma rotação do eixo para o eixo . A resultante dos dois deslocamentos deve também possuir módulo igual a , porém formando um ângulo de , medido considerando-se uma rotação de eixo para o eixo .
- Desenhe um diagrama para escala aproximada para estes vetores.
- Ache os componentes de
- Ache o módulo e a direção de
Dados:
Ver solução completaQuestão 4
Um vetor tem uma componente negativa e uma componente positiva. Seu ângulo, medido no sentido anti-horário a partir do eixo positivo, vale:
- Entre zero e graus
- Entre e graus
- Mais de graus
Questão 5
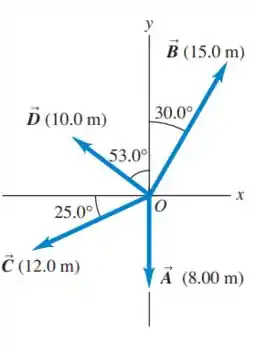
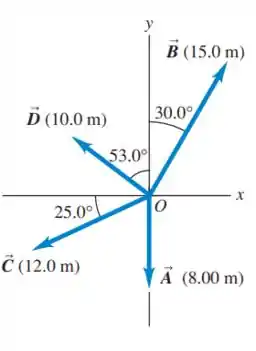
Escreva cada vetor indicado na figura abaixo em termos de vetores unitários .
Questão 6
Determine o módulo, a direção e o sentido dos vetores representados pelos seguintes pares de componentes:
Questão 7
Use componentes de vetores para determinar o módulo e a direção do vetor necessários para equilibrar os dois vetores demonstrados na Figura . Considere o vetor ao longo do eixo e considere o eixo ortogonal a ele, no sentido da direita.
Questão 8
O vetor tem componentes , ; o vetor tem componentes ,
- Encontre
- Calcule o módulo do vetor anterior
Questão 9
Determine as componentes e dos seguintes três vetores do plano .
- Um vetor deslocamento de que forma um ângulo de no sentido horário a partir do eixo
- Um vetor velocidade de que forma um ângulo de no sentido anti-horário com o eixo .
- Uma força de que forma um ângulo de no sentido anti-horário com o eixo .
Questão 10
Encontre a magnitude e a direção do vetor . Em um diagrama, mostre como é formado a partir desses vetores.
Questão 11
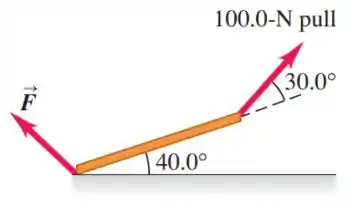
Dizemos que um objeto está em equilíbrio se todas as forças atuando nele estiverem balanceadas (somam zero). A figura abaixo mostra uma viga pesando que é apoiada em equilíbrio por um puxão de e uma força no chão. A terceira força na viga é o peso de que age verticalmente para baixo. (a) Use os componentes do vetor para encontrar a magnitude e a direção de . (b) Verifique a razoabilidade de sua resposta na parte (a) fazendo uma solução gráfica aproximadamente em escala.
Questão 12
Encontre a magnitude e a direção do vetor que é a soma dos três vetores na figura abaixo. Em uma diagrama, mostre como é formado a partir desses três vetores.
Questão 13
A posição de um elétron é dada por ; com t em segundos e r em metros . (a) Qual é a velocidade ) do elétron na notação de vetores unitários? Quanto vale no instante (b) na notação de vetores unitários e como (c) um módulo e (d) um ângulo em relação ao sentido positivo do ?
Ver solução completaQuestão 14
2. Encontre o ângulo entre as diagonais das faces de um cubo com arestas de tamanho .

Questão 15
Um carro anda para o leste, depois para o sul, depois para o oeste e, finalmente, para o norte.
- Desenhe o vetor deslocamento correspondente à posição final do carro
- Qual o módulo deste vetor e qual o ângulo formado por ele com o eixo oeste-leste?
Questão 16
A figura mostra duas forças de mesma magnitude agindo sobre um corpo. Se a magnitude comum das forças é e o ângulo é , que terceira força fará com que o corpo fique em equilíbrio.
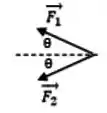
- apontando para a direita.
- apontando para a direita.
- apontando para a direita.
- apontando para a esquerda.
- apontanto para a esquerda.
Questão 18
A aceleração representada na figura fará com que a partícula
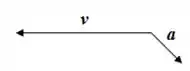
(A) Mova-se mais depressa e sua trajetória se curve para cima.
(B) Mova-se mais devagar e sua trajetória se curve para cima.
(C) Mova-se mais depressa e sua trajetória se curve para baixo.
(D) Mova-se mais devagar e sua trajetória se curve para baixo.
(E) Mova-se com rapidez constante e sua trajetória se curve para baixo.
Ver solução completaQuestão 19
Se , e , então quanto vale e em termos de vetores unitários?
- e
- e
- e
- e
- e
Questão 20
Para arrastar uma mesa de de massa, que estava no canto de sua sala, Luiza aplicou uma força sobre ela que provocou uma aceleração de a graus com o semieixo positivo. É correto afirmar que as componentes das forças resultantes nos eixos e são respectivamente iguais a:
(a) e
(b) ambas são iguais a
(c) e
(d) ambas valem
(e) e
Ver solução completaQuestão 21
A figura mostra as forças e cujos módulos são respectivamente iguais a e .
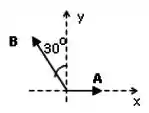
Qual a resultante ?
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 22
Um avião sai do aeroporto em Galisteo e voa a e, em seguida, muda de direção para voar , após o qual faz um pouso de emergência em um pasto. Quando o aeroporto envia uma equipe de resgate, em que direção e a que distância esta tripulação deve voar para ir diretamente a este avião?
Ver solução completaQuestão 23
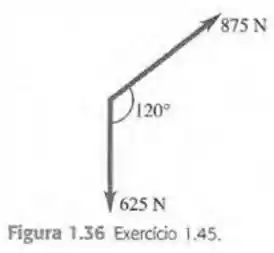
Um paciente em terapia tem um antebraço que pesa e que levanta um peso de . Essas duas forças têm direção verticalmente para baixo. As únicas outras forças significativas em seu antebraço vêm do músculo bíceps (que age perpendicularmente ao antebraço) e da força no cotovelo. Se o bíceps produz um impulso de quando o antebraço é levantado acima da horizontal, encontre a magnitude e direção da força que o cotovelo exerce no antebraço (A soma da força do cotovelo e da força do bíceps deve equilibrar o peso do braço e o peso que este está carregando, portanto, sua soma vetorial deve ser de , para cima.)
Ver solução completaQuestão 27
(Capítulo 3.4 – Exercício 7) As dimensões de uma sala são (altura) X X . Uma mosca parte de um canto da sala e pousa em um canto diagonalmente oposto. (a) Qual é o módulo do deslocamento da mosca? (b) A distância percorrida pode ser menor que este valor? (c) Pode ser maior? (d) Pode ser igual? (e) Escolha um sistema de coordenadas apropriado e expresse as componentes do vetor deslocamento em termos de vetores unitários. (f) Se a mosca caminhar, em vez de voar, qual é o comprimento do caminho mais curto para o outro canto? (Sugestão: o problema pode ser resolvido sem fazer cálculos complicados. A sala é como uma caixa; desdobre as paredes para representá-las em um mesmo plano antes de procurar uma solução.)
Ver solução completaQuestão 29
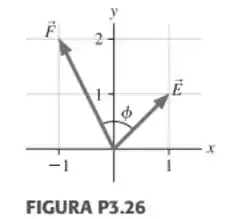
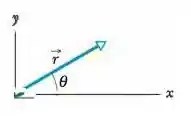
(Capítulo 3.4 – Exercício 6) Um vetor deslocamento no plano tem de comprimento e faz um ângulo com o semieixo positivo, como mostra a Fig 3-26. Determine (a) a componente e (b) a componente do vetor.
Questão 30
(Capítulo 3.4 – Exercício 1) A componente do vetor é e a componente é . (a) Qual é o módulo de ? (b) Qual é o ângulo entre a orientação de e o semieixo positivo?
Ver solução completaQuestão 31
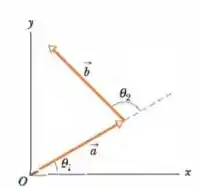
Os vetores e da Fig. 3-28 têm o mesmo módulo, , e os ângulos mostrados na figura são e . Determine as componentes (a) e (b) da soma vetorial dos dois vetores, (c) o módulo de e (d) o ângulo que faz com o semieixo positivo.
Questão 32
(Capítulo 3.6 – Exercício 8) Um carro viaja para leste, para o norte e em uma direção a leste do norte. Desenhe o diagrama vetorial e determine (a) o módulo e (b) o ângulo do deslocamento do carro em relação ao ponto de partida.
Ver solução completaQuestão 33
(Capítulo 3.6 – Exercício 11) Para os vetores e , determine (a) em termos de vetores unitários e em termos (b) do módulo e (c) do ângulo (em relação a ). Determine (d) em termos de vetores unitários e em termos (e) do módulo e (f) do ângulo.
Ver solução completaQuestão 34
Dois vetores são dados por e . Determine, em termos de vetores unitários, (a) ; (b) ; (c) um terceiro vetor, , tal que
Ver solução completaQuestão 35
Se é somado a , o resultado é um vetor no sentido do semi-eixo y positivo, com um módulo igual ao de . Qual o módulo de ?
Ver solução completaQuestão 36
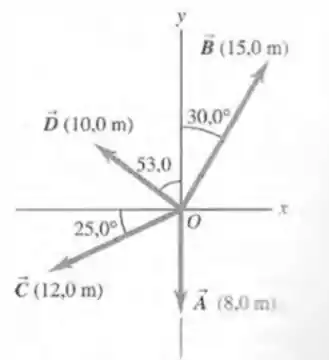
Os três vetores na Fig. 3-33 têm módulos , e ; Determine (a) a componente e (b) a componente de ; (c) a componente e (d) a componente de ; (e) a componente e (f) a componente de . Se , quais são os valores de (g) e (h) ?
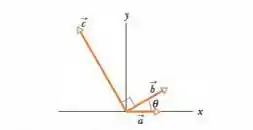
Questão 37
(Capítulo 3.4 – Exercício 4) Na Fig. 3-27, uma máquina pesada é erguida com o auxílio de uma rampa que faz um ângulo com a horizontal, na qual a máquina percorre uma distância . (a) Qual é a distância vertical percorrida pela máquina? (b) Qual é a distância horizontal percorrida pela máquina?
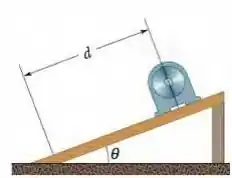
Questão 38
(Capítulo 3.6 – Exercício 9)
(a) Determine a soma , em termos de vetores unitários, para e . Determine (b) o módulo e (c) a orientação de .
Ver solução completaQuestão 39
O vetor posição de um íon é inicialmente e depois passa a ser , com todos os valores em metros. Na notação de vetores unitários, qual é a velocidade média durante os ?
Ver solução completaQuestão 40
(Capítulo 3.4 – Exercício 5) O objetivo de um navio échegar a um porto situado ao norte do ponto de partida, mas uma tempestade inesperada o leva para um local situado a leste do ponto de partida. (a) Que distância o navio deve percorrer e (b) qual o rumo deve tomar para chegar ao destino?
Ver solução completaQuestão 41
Um pósitron sofre um deslocamento e termina com o vetor posição , em metros. Qual era o vetor posição inicial do pósitron?
Ver solução completaQuestão 42
O vetor posição de um elétron é . (a) Determine o módulo de . (b) Desenhe o vetor em um sistema de coordenadas dextrogiro.
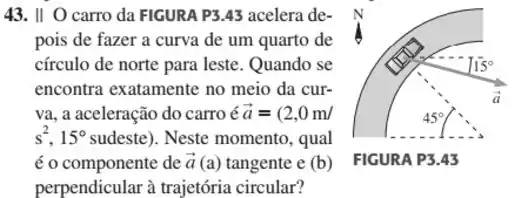
Ver solução completaQuestão 43
(Capítulo 3.4 – Exercício 3) Quais são (a) a componente e (b) a componente de um vetor do plano que faz um ângulo de no sentido anti-horário com o semieixo positivo e tem um módulo de ?
Ver solução completaQuestão 44
Uma formiga, enlouquecida pelo Sol em um dia quente, sai correndo em um plano . As componentes ( e ) de quatro corridas consecutivas em linha reta são as seguintes, todas em centímetros: , , ; . O deslocamento resultante das quatro corridas tem componentes . Determine (a) e (b) . Determine (c) o módulo e (d) o ângulo (em relação ao semieixo positivo) do deslocamento total.
Ver solução completaQuestão 45
A aceleração de uma partícula que se move apenas em um plano horizontal é dada por , onde está em metros por segundo ao quadrado e em segundos. Em , o vetor posição indica a localização da partícula, que nesse instante tem uma velocidade . Em , determine (a) o vetor posição em termos dos vetores unitários e (b) o ângulo entre a direção do movimento e o semieixo positivo.
Ver solução completaQuestão 46
O vetor está desenhado na figura ao lado. Sobre esse vetor e com base na figura, marque a alternativa incorreta:
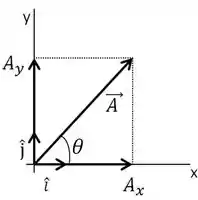
A.
B.
C.
D.
E.
Ver solução completaQuestão 47
Um pequeno esquilo atravessa um jardim, deslocando-se segundo as coordenadas e , sendo e dimensionados e em metros e em segundos. No instante , o vetor posição em termos de vetores unitários que descreve o movimento do esquilo é igual a:
a)
b)
c)
d)
e)
Ver solução completaQuestão 49
(Capítulo 3.6 – Exercício 10) Uma pessoa caminha da seguinte forma: para o norte, para o oeste e para o sul. (a) Desenhe o diagrama vetorial que representa este movimento. (b) Que distância e (c) em que direção voaria um pássaro em linha reta do mesmo ponto de partida ao mesmo ponto de chegada?
Ver solução completaQuestão 50
(Capítulo 3.6 – Exercício 11) Uma pessoa deseja chegar a um ponto que está a de sua localização atual, em uma direção ao norte do leste. As ruas por onde pode passar são todas na direção norte-sul ou na direção leste-oeste. Qual é a menor distância que a pessoa precisa percorer para chegar ao destino?
Ver solução completaQuestão 51
(a)Qual é a soma dos quatro vetores a seguir em termos de vetores unitários? (b) Para essa soma, quais são (b) o módulo, (c) o ângulo em graus, e (d) o ângulo em radianos?
Ver solução completa
Questão 53
Dado e , encontre a direção de relativo ao eixo .
A) no sentido anti horário
B) no sentido anti horário
C) no sentido anti horário
D) no sentido anti horário
E) no sentido anti-horário
Ver solução completaQuestão 54
4. Qual o gradiente de (também conhecido como magnitude do vetor
posição )?
Ver solução completaQuestão 55
1. Qual é o ângulo entre os vetores e . Dica: Lembrar quer e considerar que .
Ver solução completaQuestão 58
5. Calcule o divergente e o rotacional das seguintes funções vetoriais:
(a)
Ver solução completaQuestão 59
5. Calcule o divergente e o rotacional das seguintes funções vetoriais:
(b)
Ver solução completaQuestão 60
5. Calcule o divergente e o rotacional das seguintes funções vetoriais:
(c)
Ver solução completaQuestão 62
7. O núcleo de um átomo de ferro tem um raio de e contém . Qual é o
módulo da força de repulsão eletrostática entre dois prótons do núcleo de ferro separados por
uma distância de ? Dados: carga elétrica do próton é .
Ver solução completaQuestão 63
8. Considere três partículas, e carregadas positivamente e carregada negativamente. e estão situadas em pontos fixos do eixo , distantes por uma distância , e está entre as duas partículas a uma distância da partícula . Quais os módulos ( e
) e a orientação das forças eletrostáticas ( e ) exercidas pelas partículas e sobre a partícula e a força eletrostática total (, total) sobre a partícula ?. Dados: Carga são , e .
Ver solução completa