Força Centrípeta
Teoria
A Força centrípeta é a responsável por “puxar” o corpo para o centro da trajetória circular, quando temos um movimento circular ou curvilíneo.
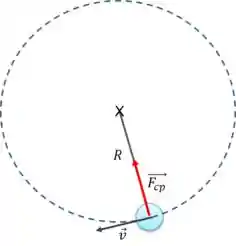
Na figura acima podemos observar a força centrípeta representada por uma seta vermelha, ela sempre aponta para o centro da trajetória circular. Para um corpo permanecer em movimento circular, ele obrigatoriamente deve estar sob ação de uma força centrípeta!
Agora, pra a gente começar com o pé direito, dá uma conferida nesse vídeozinho super completo sobre Força Centrípeta, que o Responde Aí preparou pra você 👇👇👇
Ou se você preferir, continua comigo no textinho! 😉 👇
Fórmula da Força Centrípeta
Podemos calcular a força centrípeta usando a seguinte fórmula:
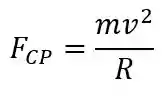
Onde:
é a massa do objeto, em ; é a velocidade do objeto, em ; é o raio da trajetória percorrida pelo corpo, em .
Aceleração Centrípeta
A aceleração centrípeta é uma componente da aceleração perpendicular à trajetória e ela é responsável pela mudança de direção.
Podemos calcular a aceleração centrípeta usando a seguinte fórmula:
Apesar do nome “aceleração”, ela não muda o módulo de velocidade do objeto.
Agora, você sabia que a fórmula da força centrípeta é uma junção entre a segunda lei de Newton e a aceleração centrípeta!?
Lembrando que, pela segunda lei de Newton:
Substituindo a aceleração centrípeta, ficamos com:
Que é exatamente a fórmula da força centrípeta que vimos ali em cima!
Aplicações da Força Centrípeta
Já sabemos o módulo, a direção e o sentido dessa força, portanto, devemos sempre lembrar que no Movimento Circular Uniforme a força centrípeta é a resultante das forças que atuam sobre o corpo apontando para o centro da trajetória.
Vamos ver uns exemplos de movimento circular uniforme pra ficar bem claro:
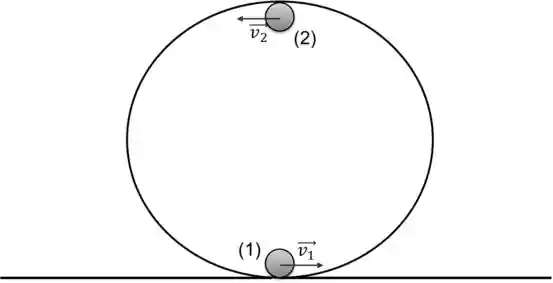
Situação 1: Considerando que a superfície do loop não tem atrito, o diagrama de corpo livre do corpo é:
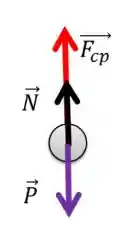
Como sempre, a força centrípeta está apontando para o centro da trajetória circular.
No entanto, ela não é uma força a mais, que você pode colocar na segunda lei de newton junto com as outras e tirar o valor dela. Ela é a resultante das forças que atuam na direção que passa pelo centro da trajetória. Portanto:
Situação 2: Agora temos o corpo no alto da trajetória, apresentando o seguinte diagrama:
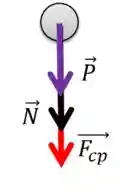
Aqui, da mesma maneira que a anterior, a força centrípeta é a resultante das outras duas forças:
Força Centrípeta e Centrifuga
Como terminamos de ver, a Força centrípeta é uma força presente em movimentos circulares, responsável por alterar a direção e/ou o sentido da velocidade linear. Já a Força centrífuga não existe do ponto de vista de um referencial inercial! Ela é uma pseudoforça que ocorre em um referencial não inercial em rotação.
Sabe quando você esta em um carro fazendo uma curva e você sente como se seu corpo fosse “puxado” pra fora da curva? É exatamente isso o que chamamos de força centrifuga!
Agora vamos praticar com exercícios?!
Fórmula da Força Centrípeta
Aplicações da Força Centrípeta
Força Centrípeta e Centrifuga
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, David, Fundamentos de física, volume 1 - mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 142-11
A Fig. 6-18 mostra a trajetória de um carrinho de parque de diversões que passa, com velocidade escalar constante, por cinco arcos circulares de raios , e . Ordene os arcos de acordo com o módulo da força centrípeta que age sobre o carrinho ao passar pelos arcos, começando pelo maior.
Passo 1
Esta é uma questão puramente conceitual, basta lembrarmos dá fórmula da força centrípeta:
Como a massa e a velocidade do carrinho são constantes, temos que a força centrípeta é inversamente proporcional ao raio.
Agora só nos falta saber quais são os raios de cada arco. A imagem abaixo vai facilitar a visualização:
Temos então que:
- Arco 4 –
- Arco 3 –
- Arco 1,2 e 5 -
Resposta
Na ordem decrescente de força centrípeta:
Exercício Resolvido #2
UNICAMP-P1-2014.2A-Q12
Um carro pequeno de massa viaja em uma pista horizontal. Como ilustrado pela figura abaixo, em certa posição a pista possui um loop, uma circunferência vertical de raio :
Qual é a aceleração mínima, para que o carro, no topo do loop não perca o contato das suas rodas com a pista?
a) , com o sentido do vetor aceleração para baixo.
b) , com o sentido do vetor aceleração para cima.
c) , com o sentido do vetor aceleração para cima.
d) , com o sentido do vetor aceleração para baixo.
e) , com o sentido do vetor aceleração para cima.
Passo 1
No topo do loop o carro estará sob a ação das seguintes forças:
No limite, quando o carro está na iminência de perder o contato com a pista, aproximamos . Logo aplicando a segunda lei de Newton:
Logo, a aceleração mínima é a aceleração da gravidade. Que é descrito na letra .
Resposta
Letra
Exercício Resolvido #3
Elaboração Própria
Homer, que possui massa , decide se aventurar no Globo da morte. Para isso ele deseja calcular a velocidade que ele pretende ficar para conseguir fazer o movimento. Como ele é “limitado” ele precisa da sua ajuda. Considerando que ele manterá uma velocidade constante , e o raio do Globo da morte é , e que o atrito neste caso é desprezível. Considere também que o módulo da aceleração da gravidade é . Determine
a) a força normal quando a moto passa na parte mais baixa do Globo.
b) a força normal quando a moto passa na parte mais alta do Globo.
c) a velocidade mínima para ele conseguir fazer a volta no Globo.
Passo 1
Os dados do problema são
Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.
a)
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Sim, o bloco está em contato com o chão.
Não, não existe um fio atuando.
Não, não existe mola atuando.
Não, não existe atrito.
Teremos então o segundo DCL na parte mais baixa do globo
Passo 2
Nesse problema, ele está fazendo uma curva. Então devemos determinar a força resultante na direção do centro da curva, que será a força centrípeta
A força resultante na direção do centro da curva é
Passo 3
b)
Vamos começar respondendo a pergunta do passo a passo para montar o DCL.
- Sim, tem massa.
- Sim, ele está apoiado no chão.
- Não temos um fio.
- Não temos mola.
- O atrito é desprezível
Teremos então o segundo DCL na parte mais alta do globo
Passo 4
Nesse problema, ele está fazendo uma curva. Então devemos determinar a força resultante na direção do centro da curva, que será a força centrípeta
A força resultante na direção do centro da curva é
Passo 5
c)
A velocidade mínima é aquela onde faz a Normal em um dado ponto ser zero. O ponto crítico no globo da morte é na parte mais alta do Globo da Morte, então
Resposta
Exercício Resolvido #4
PUCRIO-P1-B-2012.2 Q2B-letras c e d
Um bonde antigo, trafegando a , faz uma curva (plana) à direita com de raio. Neste bonde, existem alças de mão fixas ao teto, com liberdade para inclinar-se em qualquer direção.
c) Vistas por algum passageiro no fundo do bonde, em que direção as alças de mão se inclinam quando o bonde faz a curva? Justifique.
d) Qual é o ângulo que as alças de mão fazem com a vertical?
Passo 1
c)
Vamos analisar a situação utilizando a primeira lei de Newton. Um corpo que está em movimento em linha reta, vai continuar esse movimento ao menos que forças externas atuem sobre ele. No nosso caso, a alça vai tender a continuar em linha reta, enquanto que o trem irá virar para a direita. Como o observador dentro do trem está virando para a direita junto com o trem, a impressão que dá é de que ele continuou em linha reta e a alça virou para a esquerda. Mas na verdade a alça continuou em linha reta e o trem virou a direita.
Passo 2
d)
A figura mostra o diagrama de corpo livre para a alça. Neste caso, o eixo é escolhido com o sentido positivo apontado para o centro da curva e o eixo é a vertical. Assim, o ângulo procurado é o ângulo do vetor com o eixo . A segunda lei de Newton neste caso fica:
Eixo :
No eixo teremos a força centrípeta:
Dividindo a equação do eixo com a do eixo temos:
Neste caso:
Passando para , divide-se por 3,6:
Então:
Então:
Resposta
c) Para a esquerda.
d)
Exercício Resolvido #5
Elaboração Própria
Um aluno, meio nerd, decide fazer uma experiência em uma mesa de ar. Ele solta um cubo de Rubik nessa mesa, preso por um fio que passar por um furo no centro da mesa, e na outra ponta do fio está outro cubo de Rubik, como mostrado na figura. Esse cubo sobre a mesa está realizando um movimento circular, de velocidade angular . Determine o raio do movimento considerando que o cubo pendurado está em repouso, e a massa de ambos os cubos é .
Passo 1
Normalmente começamos um problema com vários blocos, fazemos o DCL do sistema. Neste caso, como temos o cubo em repouso e o cubo se movimentando circularmente, fazer o sistema pode ser algo mais complicado, então iremos montar as equações para cada bloco.
Os dados do problema são
Em problemas literais é sempre bom escrever os dados separados para mais tarde conferir se as respostas estão de acordo com esses dados.
Para o bloco
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Não, o bloco não está apoiado em nenhuma superfície.
Sim, existe um fio.
Não, não existe mola atuando.
Não, não existe atrito.
Seu DCL fica
Passo 2
Como o sistema está em repouso temos equilibro em ambos os eixos. Vamos fazer o equilíbrio no , que é o eixo onde as forças atuam.
Passo 3
Para o bloco
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Sim, o bloco está apoiado na mesa.
Sim, existe um fio.
Não, não existe mola atuando.
Não, não existe atrito, pois o bloco está sobre uma mesa de ar.
Seu DCL fica
Passo 4
Como esse cubo faz um movimento circular, sabemos que a força resultante na direção do centro da curva é a força centrípeta. A única força que está nessa direção é a tração
Para resolver essa equação precisamos da velocidade.
Passo 5
Lembrando do capitulo de movimento circular podemos relacionar a velocidade com a velocidade angular da seguinte forma
Lembrando que, nesse caso, , pois, pelo desenho, o cubo está se movendo no sentido horário. Isso não vai alterar o resultado final, mas fica aí o bizu!
Passo 6
Substituindo na equação da força centrípeta
Resposta
Exercício Resolvido #6
Halliday, David, Fundamentos de física, volume 1 - mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 147-57
Um parafuso está enroscado em uma das extremidades de uma haste fina horizontal que gira em torno de outra extremidade. Um engenheiro monitora o movimento iluminando o parafuso e a haste com uma lâmpada estroboscópica, ajustando a frequência dos lampejos até o parafuso parecer estar nas mesmas oito posições a cada rotação completa da haste (Fig. 6-46). A frequência dos lampejos é por segundo, a massa do parafuso é e a haste tem de comprimento. Qual é o módulo da força exercida pela haste sobre o parafuso?
Passo 1
Neste movimento circular, temos a haste realizando a tração que faz o parafuso continuar na trajetória, por isso, temos que:
Sabemos também que a força centrípeta é dada por:
A massa nos foi dada e o raio da trajetória é o comprimento da haste, que também nos foi dado. O que nos falta, é a velocidade que o parafuso se movimenta.
Passo 2
Nos foi dado:
- Número de piscadas por segundo:
- Número de piscadas por volta:
É interessante para nós descobrir a frequência do movimento, ou seja, o número de voltas por segundo, certo? Então vamos analisar as unidades dos dados que nos foi dado... Se dividirmos o primeiro pelo segundo dado temos:
Com a frequência do movimento, conseguimos obter a velocidade angular:
Pra finalmente obtermos a velocidade linear:
Passo 3
Com o valor da velocidade encontrado, podemos voltar com ele para a expressão da força centrípeta:
Substituindo os valores de , e :
Resposta
Exercício Resolvido #7
UNICAMP-Física I-Manhã -P1-2014.2--Questão 11
Dois corpos com massa e estão a uma distância e de um eixo. O corpo com massa está conectado por uma mola com constante elástica ao eixo e o corpo de massa está conectado ao corpo de massa por uma mola de constante elástica . Os corpos estão girando em torno do eixo com uma frequência angular , constante. Despreze as massas das molas e o efeito da aceleração gravitacional.
O que ocorre com o aumento gradual de ?
a) A mola entre os corpos sempre se rompe primeiro.
b) A mola entre o corpo e o eixo sempre se rompe primeiro.
c) A mola entre os corpos se rompe primeiro, se .
d) A mola entre os corpos se rompe primeiro, se .
e) Ambas, as molas, se rompem ao mesmo tempo.
Passo 1
O aumento gradual do afeta diretamente no aumento gradual da velocidade de acordo com a fórmula:
Como já estamos careca de saber, teremos que:
E assim:
Passo 2
Agora o seguinte: Considerar que a mola vai quebrar dá no mesmo que uma corda quebrar. Ela vai cobrar quando atingir certa força , ok? Desta forma, fazendo as equações de Newton, teremos:
Para o bloco 1, teremos:
Para o segundo bloco, vai ficar:
Passo 3
Somando os dois encontraremos que:
Mas já sabemos que
Passo 4
Desta forma, ao aumentar o o cabo onde há tração vai romper primeiro, já que massa a nunca é negativa , ou seja. Isso nos diz que a mola entre o bloco 1 e o eixo vai romper primeiro. :P
Resposta
Letra B de Bola.
Exercício Resolvido #8
Halliday, David, Fundamentos de física, volume 1 - mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 145-41
Qual é o menor raio de uma curva sem compensação (plana) que permite que um ciclista a faça a curva sem derrapar se o coeficiente de atrito estático entre os pneus e a pista é de ?
Passo 1
Esta situação é igual àquela citada na teoria, onde temos um carro entrando em uma curva, no entanto, os dados dados foram diferentes.
O enunciado facilitou nossa vida fornecendo somente o coeficiente de atrito estático. Por que? É comum os alunos confundirem e, para essa situação usar o coeficiente de atrito dinâmico, só porque o corpo está em movimento.
A relação ainda é a mesma:
Passo 2
Sabemos que somente não há movimento na vertical, ou seja, o ciclista não está pulando e nem dando uma de tatu, perfurando o chão. Portanto, pela segunda lei de Newton:
Subsituindo na primeira expressão encontrada:
Agora é só substituir os valores! Lembrando de converter a velocidade dada para , dividindo-a por :
Resposta
Exercício Resolvido #9
UFF-P1-2014.1-10M
Em um dia gelado de inverno, o coeficiente de atrito entre os pneus de um carro e a estrada é reduzido a um quarto do seu valor em dia seco. Como resultado, a rapidez máxim na qual o carro pode percorrer com segurança a mesma curva de raio é igual a
reduzida de uma quantidade desconhecida que depende da massa do carro.
Passo 1
Para determinar a razão entre as velocidades, vamos primeiro determiná-las em função de paramestros conhecidos, ou que possamos cortar no fim!
Para um dia seco:
A força centrípeta é dada por:
Logo:
Para um dia gelado, temos:
Agora, a força centrípeta é:
Logo:
A razão será:
Resposta
Exercício Resolvido #10
UFRJ-Física 1-P1 2013.2 ME9
Os pneus de um carro de massa têm coeficiente de atrito estático com a pista horizontal de uma rodovia em uma curva circular de raio . A velocidade máxima com que o corpo pode fazer essa curva sem derrapar é . Supondo que o carro faça a curva com velocidade de módulo constante , podemos dizer que, nesse caso, a força de atrito estático entre os pneus e a pista tem módulo igual a
Passo 1
Vamos começar analisando o movimento com velocidade
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Sim, o bloco está em contato com o chão.
Não, não existe um fio atuando.
Não, não existe mola atuando.
Sim, existe atrito.
A grande dúvida é para onde ficara o atrito?
Nesse problema se consideramos apenas o peso e a normal teremos forças na vertical, a curva é feita na horizontal, então a curva é feita pela força de atrito. Isso nós diz que a força de atrito aponta para o centro da curva.
OBS:
A força de atrito de uma roda com uma superfície não é considerada a força de atrito dinâmica, mas sim a força de atrito estática. Por quê? Porque a roda não está arrastando no chão, mas sim tocando nele.
O DCL do carro fica
Passo 2
A força de atrito é a única força que atua na direção do centro da curva logo
A força centrípeta na primeira situação é
Então
Passo 3
Quando mudamos o movimento, o DCL fica exatamente igual, porém mudandando a velocidade iremos mudar a força centrípeta, e conseqüentemente a força de atrito. Ainda teremos
Vamos calcular a com a nova velocidade
Então
É importante entender que a força de atrito estática NÃO é dada pela fórmula. O que a fórmula nos diz é a força de atrito MÁXIMA.
Resposta
Letra B
Exercício Resolvido #11
UFRJ-Prova Final-2014.2-Múltipla Escolha n°5
Um pêndulo cônico é constituído por uma partícula presa a um fio ideal que faz um ângulo com a vertical, de modo que a partícula esteja em movimento circular uniforme em um plano horizontal com o centro da trajetória no ponto da vertical, como indica a figura. Em um dado instante, em que a partícula está em um ponto , sua aceleração é um vetor de
(a) módulo , vertical apontando pra baixo
(b) módulo , apontando de pra
(c) módulo , apontando de pra
(d) módulo , apontando de pra
(e) módulo , apontando de pra
Passo 1
Num movimento circular, tem a aceleração tangencial, tangente ao movimento, e a aceleração centrípeta, que aponta pro meio da trajetória.
Mas o movimento é circular uniforme! Isso significa que o módulo da velocidade da partícula não varia, então a partícula não tem aceleração tangencial. Portanto, a sua aceleração é só centrípeta.
Ou seja, o vetor aceleração da partícula aponta de pra .
Show, só assim de bobeira já eliminamos 3 alternativas!
Passo 2
E já que estamos falando de aceleração, por que não usar a 2ª lei de Newton? As únicas forças atuando na partícula são seu peso e a tração no fio :
Passo 3
Mas já que a aceleração é só centrípeta, a boa é decompor essas forças pra elas terem uma componente centrípeta. No caso a não dá pra decompor porque ela já é perpendicular à direção centrípeta, mas a dá!
Vou considerar esse triângulo que tá aparecendo aí na figura de cima. Aplicando uma trigonometria básica, a decomposição da força vai ser:
Passo 4
A força resultante na direção centrípeta é , então, pela 2ª lei de Newton:
Mas já vimos que a aceleração total da partícula é igual à sua aceleração centrípeta, então podemos trocar por , o que dá:
Então pra achar , precisamos do valor de !
Passo 5
A partícula não tem movimento no sentido vertical, então as forças e se cancelam:
E , então:
Passo 6
Show! Então vamos ter:
Resposta
Alternativa (d)
Exercício Resolvido #12
USP- P1-2012-Questão3
Você está dirigindo um carro em uma pista circular de raio , que é inclinada de um ângulo com a horizontal, como indicado na Figura. A velocidade do carro é , constante em módulo.
(a) Faça um diagrama de forças considerando que não existe nenhum tipo de atrito entre os pneus do carro e a pista.
(b) Calcule a velocidade na ausência de atrito em função de , e .
(c) Considerando que mesmo com o carro andando há uma força de atrito do tipo estático (de coeficiente ) entre os pneus do carro e a pista, que evita que o carro deslize para baixo ou para cima. Faça o diagrama de forças nestes dois casos.
(d) Com o atrito descrito no item (c) entre o pneu do carro e a pista, determine a velocidade mínima e máxima que o carro pode ter para que este não deslize.
Passo 1
(a)
Sem a força de atrito teremos apenas a força normal e a força peso , formando uma força resultante centrípeta .
Passo 2
(b)
No caso sem atrito, temos que a componente vertical da força normal compensa exatamente a força-peso, portanto:
A força resultante será na horizontal, e será a componente horizontal da normal:
Usando , e a fórmula da aceleração centrípeta: , temos que:
Passo 3
(c)
Se o carro andar a baixa velocidade, ele correrá o risco de deslizar para baixo na pista. Logo ele precisa de uma força de atrito que o empurre para cima na pista. Ficará assim:
Além disso, o carro poderá andar a altíssima velocidade e correr o risco de sair para fora da pista. Para isso a força de atrito terá que empurra-lo de volta a pista. Então teremos também este caso:
Passo 4
(d)
Lembra que no item calculamos a velocidade do carro na pista sem atrito? Então, está velocidade é a referência para dizer se está a uma velocidade alta ou baixa. A força de atrito estático será para cima da pista se , ou para baixo da pista no caso de .
Vamos supor inicialmente o primeiro caso, de uma velocidade abaixo daquela na qual o atrito seria nulo. Temos então, pelo diagrama do item anterior, que as componentes na horizontal e na vertical são dadas por:
Na horizontal:
Na vertical:
Usando que o valor máximo da força de atrito estático é , da segunda equação encontramos que o valor máximo da normal é:
Substituindo esse resultado na primeira equação, temos que:
Como:
Obtemos:
O caso em que é totalmente análogo ao anterior, bastando que se inverta o sentido da força de atrito nas equações acima. O resultado é a mudança no sinal de :
Resposta
(a)
(b)
(c) Baixa velocidade:
Alta velocidade:
(d)
Exercício Resolvido #13
UFRJ-Física 1-P1 2013.1-Múltipla Escolha n°9
Uma partícula de massa está dentro de um funil de vidro e percorre a sua superfície inferior com um movimento circular uniforme horizontal. Não há atrito entre a parede do funil e a partícula. O ângulo que a parede do funil faz com o seu eixo de simetria é igual a , como mostra a figura. Desprezando a presença do ar, o módulo da força da superfície sobre a partícula e o módulo da aceleração centrípeta da partícula são, respectivamente,
- e
- e
- e
- e
- e
Passo 1
Vamos responder as perguntas do passo a passo para colocar as forças no DCL
- A massa dela é considerada?
- Ela está encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ela tem massa.
Sim, o sistema está apoiado no chão.
Não, não existe fio atuando.
Não, não existe mola atuando.
Não, não existe atrito
O DCL da partícula fica
Nesse caso, por mais que estejamos em um plano inclinado, como ela está rodando é importante determinarmos a resultante na direção do centro da curva. E como ele pretende que ela não caia é melhor, neste caso, usarmos os em relação ao chão e não em relação à superfície inclinada.
Estão mega confusas essas forças né? Vamos tentar ver em um esquema melhor.
Como fizemos essa mudança de ângulo?
Vamos chamar de o ângulo entre o eixo horizontal e a superfície inclinada.
Consegue perceber que
Soma dos ângulos internos de um triangulo certo? O que isso nos diz?
Repare que o ângulo que a normal faz com o eixo horizontal somado com é igual a . Então esse ângulo deve ser , pela fórmula ali em cima.
Voltando à física.
Passo 2
Vamos fazer o equilíbrio no
Vamos achar a componente da , usando a “regra do COlado, SEparado”.
Teremos então
Passo 3
Vamos agora ao
Sabemos que o módulo da força centrípeta deve ser igual ao módulo na componente da normal. Vamos achar o módulo de
Passo 4
Teremos então
Diferentemente do normal, escrevemos a força centrípeta assim porque o que ele quer é a aceleração centripeta mesmo, não a velocidade.
Passo 5
Vamos só reescrever aqui o que achamos
Resposta
Letra E
Exercício Resolvido #14
UFRJ-Física 1-P1-2014.1-Questão Discursiva n° 1
Uma partícula de massa é suspensa por uma mola ideal de constante elástica presa no teto. A particula gira em movimento circular uniforme horizontal, de raio e centrado na vertical que passa pelo ponto de suspensão da mola no teto, como indica a figura. A mola mantém-se reta e distendida de um comprimento (a ser determinado). A reta que passa pelo ponto de suspensão da mola e a particual mantém um ângulo constante com a vertical, descrevendo uma superfície cônica no espaço. Considere como dados , , , e o módulo da aceleração da gravidade.
- Represente em um diagrama as forças que agem sobre a partícula em um instante arbitrário.
- Calcule a distensão da mola.
- Determine o módulo da velocidade da partícula.
Passo 1
Vamos primeiro escrever os dados do problema
Vamos fazer isso para verificar depois cada resposta para ver se está de acordo com os dados do problema.
Passo 2
a)
Vamos agora fazer o DCL
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Não, o bloco não está apoiado em nenhuma superfície.
Não, não existe fio atuando.
Sim, existe uma mola.
Não, não existe atrito
O DCL fica
Passo 3
b)
Como ele está em um movimento circular, com o centro apontando na horizontal, ele está em equilíbrio no
Devemos encontrar a sua componente vertical usando a “regra do COlado, SEparado”.
Teremos
Passo 4
c)
Vamos agora fazer a analise no , isso porque a força que aponta para o centro será a força centrípeta
Devemos encontrar a sua componente vertical usando a “regra do COlado, SEparado”.
Teremos
Usando o valor que achamos para
Resposta
Exercício Resolvido #15
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp 158 -Modificado
Um pequeno bloco de massa é colocado no interior de um cone invertido que gira em torno do eixo vertical. As paredes do cone fazem um ângulo com a vertical. O coeficiente de atrito estático entre o bloco e o cone é . Para que o bloco permaneça a uma altura acima do vértice do cone, qual deve ser o valor mínimo de ?
Passo 1
Vamos responder as perguntas do passo a passo para colocar as forças no DCL
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
Sim, ele tem massa.
Sim, o sistema está apoiado no chão.
Não, não existe fio atuando.
Não, não existe mola atuando.
O DCL do bloco fica
Nesse caso, por mais que estejamos em um plano inclinado, como ele está rodando é importante determinarmos a resultante na direção do centro da curva. E como ele pretende que ele não caia é melhor, neste caso, usarmos os em relação ao chão e não em relação a superfície inclinada.
Está mega confuso essas forças né? Vamos tentar ver em um esquema melhor
Como fizemos essa mudança de ângulo? Precisamos lembrar um pouco sobre geometria. Vamos entender melhor isso
Repara que
Além disso
Então
Além disso, o ângulo do com a é um ângulo entre retas paralelas. Também sendo .
Voltando à física.
Passo 2
Vamos fazer o equilíbrio no
Vamos começar encontrando a componente da , usando a “regra do COlado, SEparado”.
Passo 3
Vamos agora achar a componente da , usando a “regra do COlado, SEparado”.
Teremos então
Passo 4
Vamos agora ao
Sabemos que o módulo da força centrípeta deve ser igual ao módulo na componente da normal menos a componente da .
Vamos primeiro achar o módulo de
Passo 5
Para o módulo da força centrípeta, devemos saber o raio do movimento também, já que a velocidade é algo que queremos descobrir.
O raio pode ser resolvido olhando para essa figura e usando trigonometria.
Passo 6
Para a componente da força de atrito, temos:
Teremos então
Resposta
Exercício Resolvido #16
P1- PUCRJ-Fisica I-2011.2- Q4
Um corpo de massa é abandonado do alto de um plano inclinado (1), que possui altura em relação ao solo, e percorre seu comprimento livre de forças de atrito até entrar em um movimento de “loop” (2), conforme mostra a figura. Use para a aceleração da gravidade.
a) Utilizando um eixo de coordenadas com a direção paralela ao plano inclinado, represente o diagrama de corpo livre para a situação na qual o corpo se encontra na posição (1) e descreva, a partir da segunda lei de Newton, as componentes das forças que atuam no corpo para cada eixo.
b) Escreva a expressão para a velocidade em função da altura de lanamento com que o corpo chega à posição (2) indicada na figura.
c) Escreva a segunda lei de Newton por componentes para a situação na qual o corpo se encontra na posição (4) com velocidade e obtenha uma expressão para a altura mínima , em função do raio , de onde o corpo deve ser lançado para que consiga completar a volta no loop.
d) Considerando que o corpo abandonado de uma altura e o loop tem um raio , sua velocidade no ponto (3) é . Calcule os módulos e direções da força normal e da força resultante que atuam no corpo ao passar naquele ponto. Use .
Passo 1
a)
O diagrama de corpo livre ficará:
Aplicando a segunda lei no eixo :
Aplicando a segunda lei no eixo :
Como a bola não se movimenta no eixo , . Logo:
Passo 2
b)
Na direção do plano, podemos aplicar a fórmula:
Substituindo:
Entretanto a questão não quer a velocidade em função do comprimento da rampa. Ele quer em função da altura. Mas podemos relacionar eles por:
Agora é só substituir:
Passo 3
c)
Na posição (4), podemos fazer o seguinte diagrama de forças.
Aplicando a segunda lei por componentes:
No eixo :
No eixo :
Lembrando que a força resultante é a força centrípeta. Então podemos substituir essa aceleração por:
Substituindo a fórmula da aceleração centrípeta:
Muito bem, no limite para se completar a volta, temos uma velocidade mínima para que o corpo não perca contato com a superfície. Essa velocidade pode ser calculada se nós tendermos a força normal (força de contato com a superfície) à zero. Portanto:
Certo, só que não queremos a velocidade mínima em função do raio, queremos a altura mínima em função do raio. Então vamos usar conservação de energia entre os pontos (1) e (4).
Agora é só substituir a velocidade que encontramos e a altura que é igual a .
Passo 4
d)
Podemos montar o seguinte diagrama de forças:
Aplicando a segunda lei de Newton por componentes:
No eixo :
No eixo :
A intensidade da força resultante será:
Direção:
Resposta
a)
b)
c)
d)
Direção horizontal.
Exercício Resolvido #17
Elaboração Própria
Uma ambulância, de massa , está em uma estrada com velocidade constante, quando ele entra em uma curva de raio . Nesse momento ele percebe que o carro está na iminência de derrapar, porém mantém a velocidade constante na curva. Qual o valor do coeficiente de atrito da roda da ambulância com a estrada para ela conseguir fazer a curva?
Passo 1
Vamos responder as perguntas do passo a passo para colocar as forças
- A massa dele é considerada?
- Ela esta encostada em alguma superfície?
- Tem algum fio?
- Tem mola?
- Tem atrito?
Sim, ele tem massa.
Sim, o bloco está em contato com o chão.
Não, não existe um fio atuando.
Não, não existe mola atuando.
Sim, existe atrito.
A grande dúvida é para onde ficara o atrito?
Nesse problema se consideramos apenas o peso e a normal teremos forças na vertical, a curva é feita na horizontal, então a curva é feita pela força de atrito. Isso nós diz que a força de atrito aponta para o centro da curva.
OBS:
A força de atrito de uma roda com uma superfície não é considerada a força de atrito dinâmica, mas sim a força de atrito estática. Por quê? Porque a roda não está arrastando no chão, mas sim tocando nele.
O DCL da ambulância fica
Passo 2
Teremos equilíbrio no , então
Passo 3
A força de atrito é a única força que atua na direção do centro da curva logo
Como ele está na iminência de derrapar, teremos
Substituindo o valor de teremos