Polias Simples
Produzido por Ludovic BeghinTeoria
Introdução
As cordas normalmente são usadas em conjunto com um sistema de polias. Vamos agora aprender sobre as polias simples. Mas, pra que servem essas polias e o que é polia simples? Vamos dar uma olhada nesse sistema aqui:
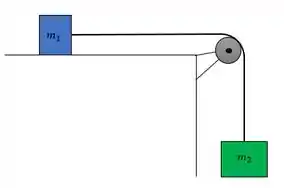
A polia é chamada de simples pois ela está fixa, ela não pode se mover. Já vimos que os fios possuem a característica de preservar a tensão nos seus dois extremos, mas estes mecanismos conseguem alterar a direção da tração. Como a corda é inextensível os blocos vão funcionar como um sistema e andarão juntos com uma certa aceleração.
Tração nos cabos e aceleração do sistema
Se a gente retirar da figura o fio e desenhar o diagrama de corpo livre de cada bloco vai ficar mais fácil de enxergar como a tração no cabo atua:
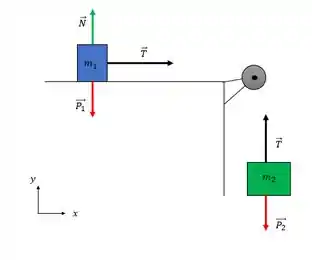
Repare que no bloco azul a tração no cabo estava na direção e usando a polia a mesma tração só que atuando no bloco verde está em E a aceleração? Como o sistema trabalha em conjunto a aceleração dos blocos são iguais e são iguais a aceleração do sistema, porém cada uma vai ter uma direção. No nosso exemplo o peso do bloco verde faz o bloco se deslocar pra baixo, e a aceleração de cada um aponta da seguinte forma:
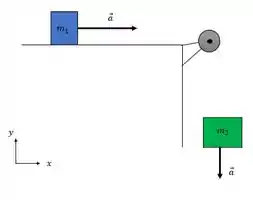
Ou seja:
Pra gente entender isso melhor, bora calcular a tração no cabo e a aceleração no sistema se e
Aqui a gente vai fazer um sisteminha, usando a segunda lei de Newton para cada bloco, começando pelo bloco azul, temos o DCL:
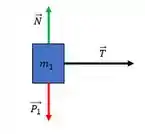
Como o bloco não se desloca em , só nos interessa o eixo . Usando a segunda lei de Newton temos:
Como no eixo só temos a força de tração a gente pode dizer que:
E aqui a gente já sabe a direção de cada coisa, então não vamos precisar da notação vetorial ou seja podemos trabalhar com os módulos.
No bloco verde o DCL é:
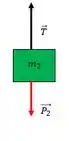
Aqui o bloco não se movimenta em , vamos trabalhar só em .
Onde é a aceleração da gravidade e vale 9,81
E pela segunda lei, considerando o sentido positivo para baixo:
Ou seja:
Substituindo a equação 1 na equação 2:
Enfim isolando a aceleração , e aqui todo os sentidos foram considerados não necessitando entrar com o sinal da gravidade.
E enfim substituindo os valores:
E a tração a gente pode tirar da primeira equação:
E se você quiser conferir se os seus resultados estão certos pode conferir na equação 2:
Máquina de Atwood
E quando os dois corpos estão na vertical? A máquina de Atwood é exatamente isso, dois corpos são unidos por uma polia simples, mas e aí como calculamos a aceleração e a tração no cabo agora? Vamos dar uma olhada no sistema:
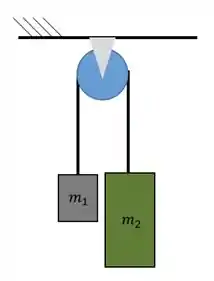
Vamos fazer o diagrama de corpo livre de cada bloco e na polia para entender bem:
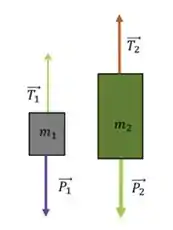
Lembre-se: a polia não muda o módulo da tração na corda, logo: .
Agora, como sabemos para determinar o sentido desse movimento? Tudo depende de qual corpo é mais pesado! Se é maior que , temos que o bloco de massa desce enquanto o de massa sobe. Caso contrário, se , o bloco 1 desce e o bloco 2 sobe.
E se não soubermos as massas? Simples! Nesse caso, fazemos uma suposição de que o movimento tem um dado sentido e se acharmos uma aceleração negativa, já sabemos que consideramos o sentido errado.
Como a polia é fixa, quando um bloco sobe uma distância , o outro desce essa mesma distância . Assim, a aceleração dos dois blocos é a mesma!
Vamos encontrar a aceleração no caso de e
Como , temos:
Para o bloco 2, o sentido positivo é pra baixo já que é o bloco de maior massa.
E para o bloco 1, o sentido positivo é pra cima!
Resolvendo o sistema formado por essas duas equações acima, temos:
E aí substituindo:
Temos a aceleração: