Exercícios de Polias Simples - Lista de Exercícios Resolvida
Questão 1
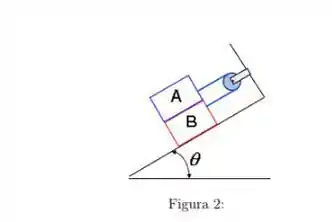
O plano abaixo tem inclinação em relação à horizontal igual a . Duas cordas inextensíveis e uma polia, ambas sem massa, mantém em equilíbrio três caixas. Despreze o atrito entre as caixas e o plano. Responda aos itens abaixo, sabendo que a caixa tem massa igual a , a caixa tem massa igual a , e que .
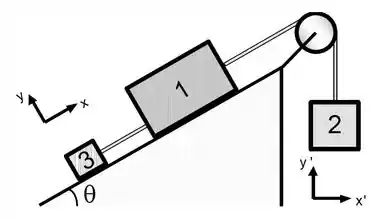
Escreva a expressão literal para as equações de movimento das três caixas, em termos das suas componentes, utilizando os respectivos sistemas de coordenadas indicados na figura. Em seguida calcule o valor da massa da caixa .
Calcule e escreva utilizando notação vetorial a força normal que a caixa exerce sobre o plano.
Suponha agora que a caixa tem massa igual a . Calcule a componente horizontal da aceleração da caixa .
Ver solução completaQuestão 2
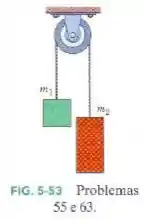
A Fig. 5-53 mostra dois blocos ligados por uma corda (de massa desprezível). O conjunto é conhecido como máquina de Atwood. Um bloco tem massa ; o outro tem massa . Quais são (a) o módulo da aceleração dos blocos e (b) a tensão na corda.
Questão 3
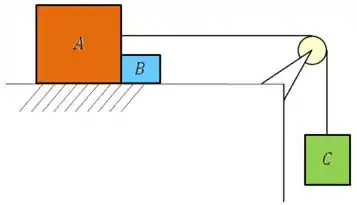
Três blocos , e , estão dispostos como o sistema mostrado na figura abaixo. Sabendo que o atrito é desprezível e as massas dos blocos são , e respectivamente. Determine a aceleração do conjunto, a força de tração no fio e a força de contato. Considere o módulo da aceleração da gravidade sendo .
Questão 4
Uma cunha, formada pela junção de duas rampas inclinadas de ângulos e , está fixa ao solo. Os blocos de massas e estão ligados por um fio ideal que passa por uma polia ideal fixa no vértice da cunha. Os blocos estão inicialmente em repouso e cada um deles encontra-se em uma das rampas, como mostra a figura.
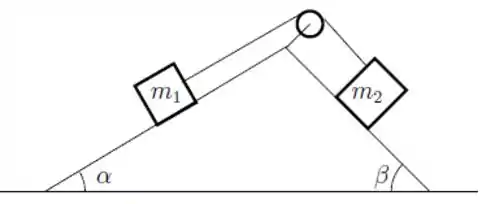
Desprezando o atrito entre os corpos e as superfícies das rampas
a) desenhe o diagrama de forças para cada um dos blocos, separadamente;
b) supondo que as massas sejam tais que o bloco de massa desça a rampa à esquerda, determine o módulo da aceleração ;
c) obtenha a razão para que o sistema permaneça em repouso;
d) de acordo com o item (c), qual o valor da tração no fio?
Ver solução completaQuestão 5
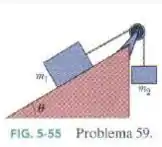
Um bloco de massa sobre um plano sem atrito inclinado, de ângulo , está preso por uma corda de massa desprezível, que passa por uma polia de massa e atrito desprezíveis, a um outro bloco de massa (Fig 5-55). Quais são (a) o módulo da aceleração de cada bloco, (b) a orientação da aceleração do bloco que está pendurado e (c) a tensão da corda?
Questão 6
Inicialmente o sistema de corpos mostrado na figura parte do repouso. Todas as superfícies, polia e rodas são sem atrito. O corpo de massa é preso ao corpo de massa , podendo deslizar verticalmente sem atrito, mas não podendo se afastar dele.
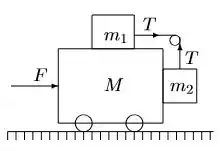
a) Qual é a força horizontal que tem de ser aplicada ao carro para que os blocos permaneçam estacionários em relação ao carro?
Para , no instante após ser solto o sistema de corpos, encontre:
b) A tensão no fio.
c) A aceleração de .
d) A aceleração de .
e) A aceleração de .
Ver solução completaQuestão 7
Um pintor de está sobre uma plataforma de suspensa por uma roldana ideal (veja a figura abaixo). Puxando a corda ele faz a plataforma subir com aceleração de .
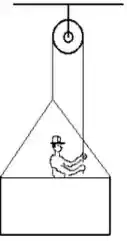
Desenhe o diagrama de forças que atuam no pintor e na plataforma e escolha um sistema de referência.
Escreva as leis de Newton para o pintor e para a plataforma.
Determine cada uma das forças que atuam no pintor.
Determine cada uma das forças que atuam na plataforma.
Ver solução completaQuestão 8
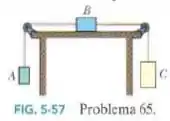
A Fig. 5-57 mostra três blocos ligados por cordas que passam por polias sem atrito. O bloco B está sobre uma mesa sem atrito; as massas são e . Quando os blocos são liberados qual é a tensão da corda da direita?
Questão 9
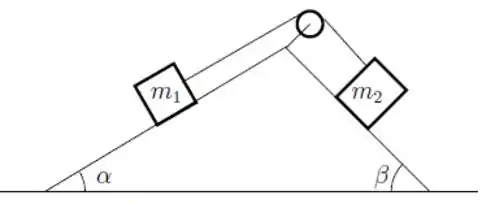
Uma cunha, formada pela junção de duas rampas inclinadas de ângulos e , está fixa ao solo. Os blocos de massas e estão ligados por um fio ideal que passa por uma polia ideal fixa no vértice da cunha. Os blocos estão inicialmente em repouso e cada um deles encontra-se em uma das rampas, como mostra a figura.
Desprezando o atrito entre os corpos e as superfícies das rampas
a) desenhe o diagrama de forças para cada um dos blocos, separadamente;
b) supondo que as massas sejam tais que o bloco de massa desça a rampa à esquerda, determine o módulo da aceleração ;
c) obtenha a razão para que o sistema permaneça em repouso;
d) de acordo com o item (c), qual o valor da tração no fio?
Ver solução completaQuestão 10
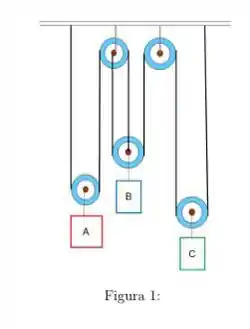
Determine as acelerações de cada bloco da Fig.(1), considerando que as massas dos blocos A, B e C são respectivamente: e .
Questão 11
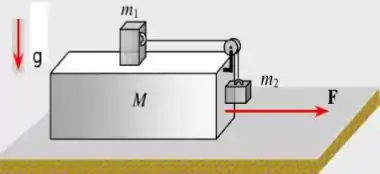
A figura abaixo representa um sistema de três blocos, de massas , e . Os blocos de massas e estão ligados por um fio ideal que passa por uma polia de massa desprezível, e o bloco de massa está em contato com o bloco de massa . O sistema é acelerado por uma força que atua no bloco de massa . Não há nenhum tipo de atrito no sistema.
a) Desenhe todas as forças que atuam nos três blocos, com especial atenção aos pares de ação e reação.
b) Considerando que o bloco de massa não desliza sobre o bloco de massa , determina a aceleração do sistema como função somente das massas e da aceleração da gravidade.
c) Calcule a força necessária para que os blocos 1 e 2 não deslizem.
Ver solução completaQuestão 12
Inicialmente o sistema de corpos mostrado na figura parte do repouso. Todas as superfícies, polia e rodas são sem atrito. O corpo de massa é preso ao corpo de massa , podendo deslizar verticalmente sem atrito, mas não podendo se afastar dele.
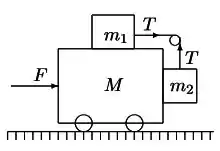
a) Qual é a força horizontal que tem de ser aplicada ao carro para que os blocos permaneçam estacionários em relação ao carro?
Para , no instante após ser solto o sistema de corpos, encontre:
b) A tensão no fio.
c) A aceleração de .
d) A aceleração de .
e) A aceleração de .
Ver solução completaQuestão 13
Na figura abaixo tem-se uma massa que está conectada a uma massa através das polias e que tem massas despreziveis. Supondo que a massa desliza sobre a mesa sem atrito e que a aceleração da massa é vertical e para baixo, pede-se:
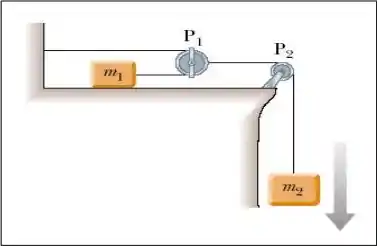
(a) Coloque em um diagrama todas as forças que atuam no sistema.
(b) Determinar o valor numérico da razão , considerando os fios inextensíveis.
(c) Determinar as trações e em função de , e .
(d) Determinar as acelerações e .
Ver solução completaQuestão 14
Considere o sistema com plano inclinado envolvendo polias esquematizado na figura abaixo. Não considere atrito. Assuma também que a massa das polias e dos fios são desprezíveis em comparação às massas e dos blocos e , respectivamente. Além disso, os fios não se esticam ou se deformam em geral. Note que a polia que sustenta o bloco está conectada ao fio ligado ao bloco e, assim, essa polia não está fixa.
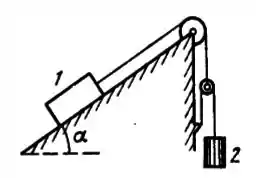
Esboce o diagrama das forças envolvidas, escreva a relação entre as diferentes tensões nos fios, e expresse a Segunda Lei de Newton para cada caso.
Demonstre a relação entre a aceleração do bloco e a aceleração do bloco .
Encontre o valor do ângulo no qual muda de sinal.
Obtenha a expressão geral para
Calcule o valor nos limites: e .
Ver solução completaQuestão 15
O sistema representado na figura abaixo pode ser usado para medir a aceleração do sistema. Um observador se movendo na plataforma mede o ângulo que o fio que suporta a bola de luz faz com a vertical. Não existe atrito em nenhum lugar. (a) Como está relacionado com a aceleração do sistema? (b) Se e o que é ? (c) Se você pudesse alterar qual é o maior ângulo que você poderia obter? Explique como você deve ajustar para fazer isso.
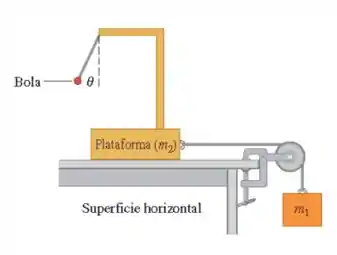
Questão 16
O plano abaixo tem inclinação em relação à horizontal igual a . Duas cordas inextensíveis e uma polia, ambas sem massa, mantém em equilíbrio três caixas. Despreze o atrito entre as caixas e o plano. Responda aos itens abaixo, sabendo que a caixa tem massa igual a , a caixa tem massa igual a , e que .
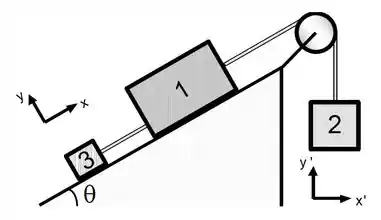
Escreva a expressão literal para as equações de movimento das três caixas, em termos das suas componentes, utilizando os respectivos sistemas de coordenadas indicados na figura. Em seguida calcule o valor da massa da caixa .
Calcule e escreva utilizando notação vetorial a força normal que a caixa exerce sobre o plano.
Suponha agora que a caixa tem massa igual a . Calcule a componente horizontal da aceleração da caixa .
Ver solução completaQuestão 17
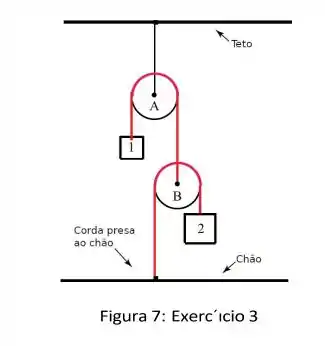
Considere o mecanismo apresentado na figura, onde o bloco 1 está apoiado em uma superfície sem atrito e o bloco 2 está sustentado por uma polia móvel sem massa (corpo 3 na figura). A polia fixa é ideal. O fio (ideal) conecta o bloco 1 à polia móvel e está fixo ao teto. O fio (ideal) sustenta o bloco 2 à polia 3.
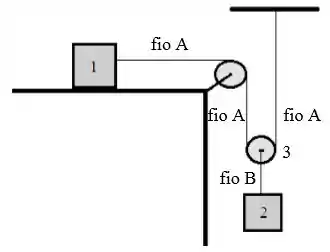
Neste mecanismo, devido ao vínculo existente entre o fio e a polia móvel, o módulo da aceleração do bloco 1, é o dobro do módulo da aceleração do bloco 2, .
As massas dos blocos são e . A massa da polia móvel . Use .
a) Represente os diagramas de corpo livre para os blocos 1 e 2 e para a polia móvel 3, explicitando todas as forças que atuam neles.
b) Escolha sistemas de coordenadas adequados para cada corpo (explicite-os!) e escreva as equações literais (não substitua ainda os valores das massas ou !) resultantes das leis de Newton para os três corpos.
c) A partir das equações do item obtenha literalmente e então substitua os valores fornecidos para encontrar o valor numérico do módulo de .
d) Obtenha o módulo da tração exercida pelo fio sobre o bloco 2.
Ver solução completaQuestão 19
Duas massas desiguais, e , com , estão conectadas por um fio leve que passa por uma polia de massa desprezível. Quando liberado, o sistema acelera. O atrito é desprezível. Qual das figuras abaixo dá os diagramas de corpo livre corretos para as massas em movimento?
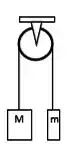
a)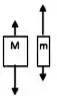
b) 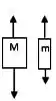
c) 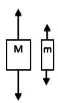
d) 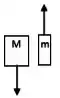
e)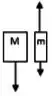
Questão 22
Em um máquina de Atwood dois blocos de massa e estão ligados por uma corda de massa desprezível que passa por uma polia de raio R = 10 cm e massa .
a) Se não há deslizamento entre a corda e a polia, calcule a tração em cada trecho da corda que liga os blocos e a força no suporte que liga a polia ao teto.
b) Se abandonados do repouso, calcule a velocidade dos blocos depois que o bloco mais pesado desce uma distância de .

Questão 23
Na figura, o fio e a roldana são ideais, e o plano fixo em que se apoia o bloco possui inclinação com a horizontal. Em todas as situações abaixo, o fio permanece tensionado e , mas o bloco pode variar. Quando necessário substituir valores, use .
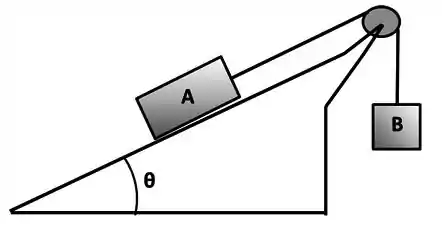
Neste item, despreze o atrito e suponha que o bloco possui aceleração para baixo. Represente o diagrama das forças que atuam sobre cada bloco e escreva as equações de movimento para ambos (deixe as equações literais e não as resolva).
Neste item, despreze o atrito e considere . Se o sistema parte do repouso e nos primeiros o bloco atinge a velocidade de para baixo, calcule a tensão no fio e a inclinação do plano.
Ver solução completaQuestão 24
Na figura ao lado um bloco de massa desliza sobre um plano horizontal com coeficiente de atrito cinético . Ele está ligado por uma corda ideal, que passa por uma polia (disco uniforme de raio e massa ), a um outro bloco de massa que está suspenso. Considere que a corda não escorrega na polia, e que não há atrito no eixo da polia. O sistema é solto do repouso em e as massas entram em movimento.
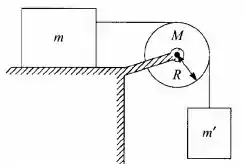
b) Qual a velocidade linear dos blocos e a velocidade angular da polia após o bloco descer uma altura ? A velocidade angular é positiva ou negativa nesse caso?
Ver solução completaQuestão 25
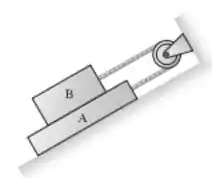
Se e , qual é a tensão na corda que conecta dos dois blocos da figura abaixo? Suponha que não há atrito entre as superfícies e que a massa da corda seja desprezível.
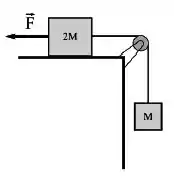
Dado:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 26
Duas massas e são ligadas por um fio sem massa. A massa desliza por uma superfície horizontal sem atrito e desce por uma polia sem massa e sem atrito. Qual será a massa pendente se a massa e a tração no fio forem conhecidas?
A.
B.
C.
D.
E.
Ver solução completaQuestão 28
Dois blocos de massa estão unidos por um fio de massa desprezível que passa por uma roldana com um eixo fixo. Inicialmente o sistema estava em repouso. Um terceiro bloco de massa é então colocado suavemente sobre um dos blocos, como mostra a figura a seguir.
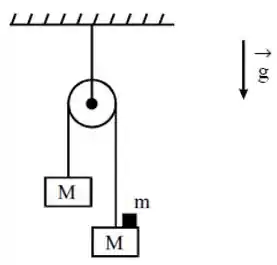
a) Faça um desenho esquemático mostrando as forças que atuam em cada um dos três blocos.
b) Qual é o módulo da aceleração adquirida pelo sistema após o bloco de massa ser colocado?
c) Supondo que o bloco da esquerda estava a uma altura abaixo do bloco da direita quando o terceiro bloco foi posicionado, determine o instante de tempo no qual os dois blocos se cruzarão.
d) Qual é o módulo da força com a qual esse pequeno bloco de massa pressionará o bloco sobre o qual foi colocado?
Ver solução completaQuestão 29
Três massas, , e estão penduradas nas cordas de polias como mostra a figura, A massa é maior que a soma das outras duas outras massas. As cordas e as polias têm massa desprezível.
a) Isole os corpos e desenhe o diagrama de forças atuando em cada massa.
b) A partir da lei de Newton escreva as equações de movimento para cada massa.
c) Encontre a aceleracao da massa .
d) Encontre as tensões nas cordas ligadas às massas e .

Questão 30
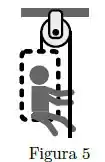
Uma pessoa está sentada em uma cadeira presa a uma corda de massa desprezível que passa por uma roldana de massa e atrito desprezíveis e desce de volta às mãos desta pessoa, conforme a Figura 5. Assuma que o peso total do sistema pessoa cadeira é . Para que a cadeira suba com velocidade constante, o homem deve puxar a corda com uma força de módulo igual a:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(j)
(k)
Ver solução completaQuestão 31
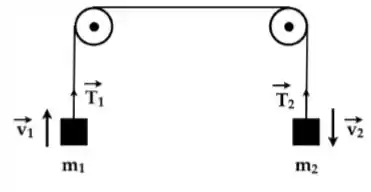
A figura abaixo mostra um esquema de polias ideais que sustentam os blocos e de massas e , respectivamente. Sabe-se que o bloco de massa movimenta-se para cima com velocidade constante. Sobre as grandezas físicas associadas a este sistema, podemos afirmar:
(a)
(b)
(c) e
(d)
(e)
Ver solução completaQuestão 33
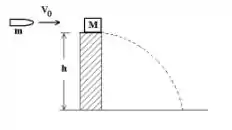
Uma partícula de massa e velocidade de é disparada contra um bloco de massa como mostra a Fig.(3). O bloco se encontra em repouso na borda de um poste de altura de . Considerando que o coeficiente de restituição , determine (a) as velocidades após a colisão (b) Determine a velocidade em que o bloco atinge o solo, desprezando a resistência do ar.
Questão 34
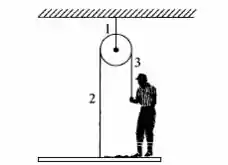
Um pintor está sobre uma plataforma suspensa de uma polia. Puxando a corda em 3, ele faz a plataforma subir com aceleração g/4. A massa do pintor é de 80 Kg e a da plataforma é de 40 Kg. Calcule as tensões nas cordas 1,2 e 3 e a força exercida pelo pintor sobre a plataforma.
Questão 35
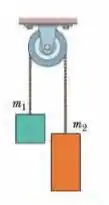
(Capítulo 5.9 – Exercício 55) A Fig. 5-47 mostra dois blocos ligados por uma corda (de massa desprezível) que passa por uma polia sem atrito (também de massa desprezível). O conjunto é conhecido como máquina de Atwood. Um bloco tem massa ; o outro tem massa . Quais são (a) o módulo da aceleração dos blocos e (b) a tensão da corda?
Questão 37
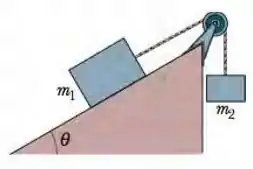
(Capítulo 5.9 – Exercício 59) Um bloco de massa sobre um plano sem atrito inclinado, de ângulo , está preso por uma corda de massa desprezível, que passa por uma polia de massa e atrito desprezíveis, a um outro bloco de massa (Fig. 5-52). Quais são (a) o módulo da aceleração de cada bloco, (b) o sentido da aceleração do bloco que está pendurado e (c) a tensão da corda?
Questão 38
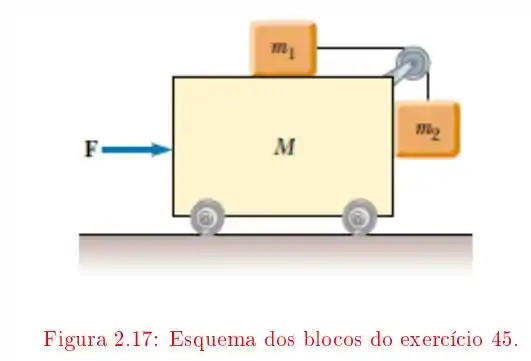
Na figura , os blocos estão ligados por fio e roldana ideais e podem deslizar sem atrito sobre as paredes do carrinho de massa . Qual o valor da força, aplicada ao carrinho, a partir do repouso, que faz com que fique parado em relação a ?
Questão 39
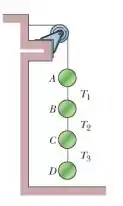
(Capítulo 5.9 – Exercício 54) Na Fig. 5-46, três caixas são conectadas por cordas, uma das quais passa por uma polia de atrito e massa desprezíveis. As massas das caixas , , . Quando o conjunto é liberado a partir do repouso, (a) qual é a tensão da corda que liga a e (b) que distância percorre nos primeiros (supondo que não atinja a polia)?

Questão 40
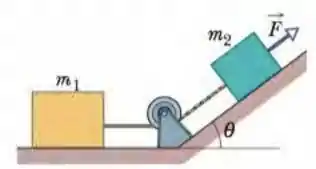
(Cap 5 – Ex 82) Na Fig. 5-64, uma força de módulo é aplicada a uma caixa de massa . A força é dirigida para cima paralelamente a um plano inclinado de ângulo . A caixa está ligada por uma corda a outra caixa de massa situada sobre o piso. O plano inclinado, o piso e a polia não tem atrito e as massas da polia e as massas da polia e da corda são desprezíveis. Qual é a tensão da corda?
Questão 41
Considere uma partícula em queda livre,
(b) Escreva a equação da energia mecânica.
Ver solução completaQuestão 42
Os dois blocos da Fig.(2) partem do repouso e suas massas são: e . Sabendo que , determine (a) a aceleração de cada bloco e a tensão no cabo. Despreze as massas das polias e os atritos.
Questão 43
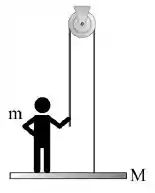
Um homem está sobre uma plataforma. O homem mantém a plataforma em repouso através de uma corda que passa por uma polia presa ao teto, como na figura. As massas da corda e da polia podem ser desprezadas, assim como o atrito na polia. Se o homem tem massa e a plataforma tem massa , qual é o módulo da força que o homem precisa fazer para manter a plataforma em repouso? (Dica: Faça diagramas de corpo livre antes de responder!)
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 44
(Capítulo 5.9 – Exercício 60) A fig.5-53 mostra um homem sentado em uma cadeira presa a uma corda de massa desprezível que passa por uma roldana de massa e atrito desprezível e desce de volta às mãos do homem.

A massa total do homem e da cadeira é 95,0 kg. Qual é o módulo da força com o qual o homem deve puxar a corda para que a cadeira suba
a) Com velocidade constante
b) Com uma aceleração para cima de 1,30 m/s²? (Sugestão: um diagrama do por livre pode ajudar bastante).
Se no lado direito a corda estende até o solo e é puxada por uma outra pessoa, qual é o módulo da força com a qual essa pessoa deve puxar a corda para que o homem suba.
c) Com velocidade constante
d) Com uma aceleração para cima de 1,30 m/s² ?
Qual é o módulo da força que a polia exerce sobre o teto
e) No item a
f) No item b
g) No item c
h) No item d
Ver solução completaQuestão 45
(Capítulo 9.1 – Exercício 74) No sistema mostrado na figura, o bloco de está sobre a prateleira horizontal. O coeficiente de atrito cinético entre a prateleira e o bloco é . O bloco está preso a um cordão que passa pela polia e tem sua outra extremidade presa a um bloco pendente de . A polia é um disco uniforme de de raio e de massa. Determine a aceleração de cada bloco e as tensões no cordão.

Questão 46
Dois blocos conectados por uma corda passando por uma pequena polia, sem atrito, e em repouso num plano também sem atrito (veja a figura abaixo).
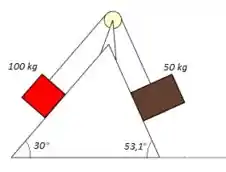
(c) Qual a tensão da corda?
Ver solução completaQuestão 47
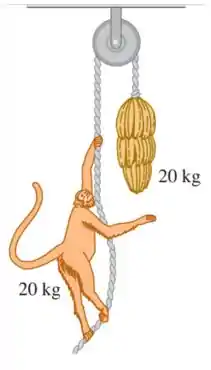
Um macaco de está segurando firmemente uma corda leve que passa sobre uma polia sem atrito e que está presa a um cacho de bananas de (Figura abaixo). O macaco olha pra cima, vê as bananas, e começa a subir a corda para ir até elas. (a) Enquanto o macaco sobe, as bananas sobem, descem ou ficam paradas? (b) Enquanto o macaco sobe, a distância entre ele e as bananas diminui, aumenta ou permanece constante? (c) O macaco solta a corda, o que acontece com a distância entre o macaco e as bananas enquanto ele cai? (d) Antes de chegar no chão, o macaco segura a corda para parar de cair. O que acontece com as bananas?
Questão 48
Dois blocos de massa e , estão presos num sistema de cordas e polias de massa desprezíveis. Calcule a aceleração do bloco , em termos das constantes do problema e da magnitude da aceleração da gravidade .
Questão 49
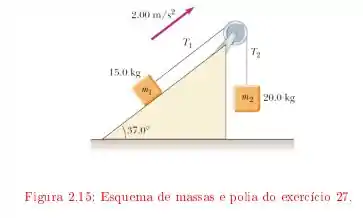
Dois blocos estão ligados por um fio de massa desprezível passando sobre uma polia de raio e momento de inércia . O bloco sobre o plano inclinado sem atrito está subindo com uma aceleração constante de .
Encontre o momento de inércia da polia.
Questão 50
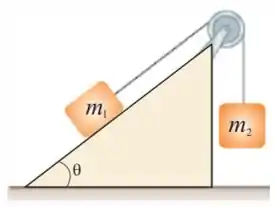
36. Um bloco de massa , que pode deslizar com atrito desprezível sobre um plano inclinado de inclinação em relação à horizontal, está ligado por um fio, que passa sobre uma polia de raio e massa , a uma massa suspensa . O sistema é solto em repouso. Calcule, por conservação da energia, a velocidade de após cair de uma altura .
Questão 51
Uma pessoa precisa levantar verticalmente um bloco de 150 kg com velocidade constante. Despreze as inércias das polias e da corda e os atritos
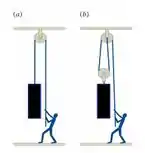
a) Qual a forca necessária para puxar a corda na situação descrita na figura (a)?
b) Considere agora a situação da figura (b) e desenhe o diagrama de corpo livre nas duas polias.
c) Se ela usar as polias como na figura (b) qual será a força necessária para levantar o bloco?
d) Na situação em que o levantamento ocorre com aceleração 0,1g qual a força necessária?
Ver solução completaQuestão 52
Um pintor está sobre uma plataforma suspensa por uma polia (figura). Puxando a corda em , ele faz a plataforma subir com aceleração . A massa do pintor é de e a plataforma tem . Calcule as tensões nas cordas e e a força exercida pelo pintor sobre a plataforma.
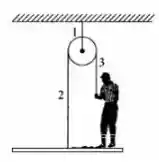
Questão 53
18. Considere o sistema descrito na figura acima à direita. Se , e o coeficiente de atrito entre o bloco de massa e a superfície é , resolva:
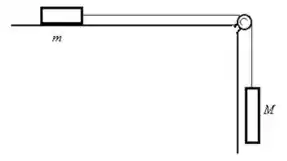
a) Faça um diagrama das forças que atuam sobre os blocos, escolha um referencial e escreva as forças nesse referencial.
Ver solução completaQuestão 54
18. Considere o sistema descrito na figura acima à direita. Se , e o coeficiente de atrito entre o bloco de massa e a superfície é , resolva:
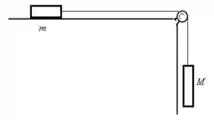
b) Calcule as forças que atuam nos blocos.
Ver solução completaQuestão 55
18. Considere o sistema descrito na figura acima à direita. Se , e o coeficiente de atrito entre o bloco de massa e a superfície é , resolva:
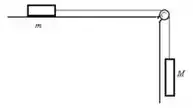
d) Calcule o trabalho dessas forças em um deslocamento de .
Ver solução completaQuestão 56
18. Considere o sistema descrito na figura acima à direita. Se , e o coeficiente de atrito entre o bloco de massa e a superfície é , resolva:
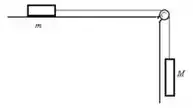
e) Considerando que na situação inicial os blocos estão em repouso, qual seria a variação de energia cinética do sistema em um deslocamento de ?
Ver solução completaQuestão 57
18. Considere o sistema descrito na figura acima à direita. Se , e o coeficiente de atrito entre o bloco de massa e a superfície é , resolva:
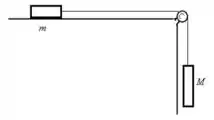
c) Calcule a aceleração dos blocos.
Ver solução completaQuestão 58
Um bloco de massa , que repousa sobre uma superfície horizontal lisa, é ligado a um bloco de massa por uma corda leve que passa por uma polia de massa desprezível, que pode girar sem atrito. O bloco de massa está ligado a uma mola de constante elástica que tem uma das extremidades fixa em uma parede vertical como mostra a figura. Se os blocos são liberados a partir do repouso com a mola na posição relaxada, calcule qual é a maior velocidade atingida pelos dois blocos. Dê sua resposta em metros por segundo.
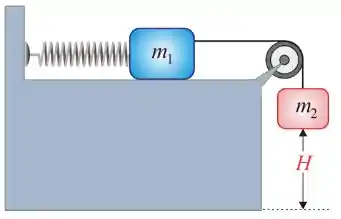
Considere os blocos como partículas.
Máximos e Mínimos de uma função são caracterizados pelo fato de que a derivada da função se anula em tais pontos.
Adote para a aceleração da gravidade
a)
b)
c)
d)
e)
Ver solução completaQuestão 59
Três caixas são conectadas por cordas, uma das quais passa por uma polia de atrito e massa desprezíveis. As massas das caixas são , e . Quando o conjunto é liberado a partir do repouso.
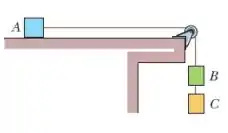
que distância percorre nos primeiros (supondo que não atinja a polia)?
Ver solução completaQuestão 60
Três caixas são conectadas por cordas, uma das quais passa por uma polia de atrito e massa desprezíveis. As massas das caixas são , e . Quando o conjunto é liberado a partir do repouso.
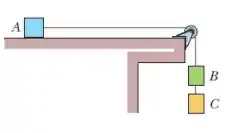
que distância percorre nos primeiros (supondo que não atinja a polia)?
Ver solução completaQuestão 61
A figura mostra dois blocos ligados por uma corda (de massa desprezível) que passa por uma polia sem atrito (também de massa desprezível). O conjunto é conhecido como máquina de Atwood. Um bloco tem massa , o outro tem massa .
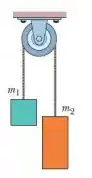
Qual é o módulo da aceleração dos blocos?
Ver solução completaQuestão 62
A figura mostra dois blocos ligados por uma corda (de massa desprezível) que passa por uma polia sem atrito (também de massa desprezível). O conjunto é conhecido como máquina de Atwood. Um bloco tem massa , o outro tem massa .
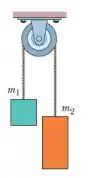
Qual é a tensão da corda?
Ver solução completaQuestão 63
A figura mostra um arranjo no qual quatro discos estão suspensos por cordas. A corda mais comprida, no alto, passa por uma polia sem atrito e exerce uma força de sobre a parede à qual está presa. As tensões nas cordas mais curtas são , e . Quais são as massas do disco e ?