Exercícios de Segunda Lei de Newton - Lista de Exercícios Resolvida
Questão 1
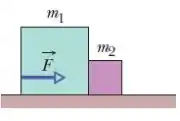
A Fig. 5-24 mostra o diagrama de corpo livre de quatro situações nas quais um objeto, visto de cima, é puxado por várias forças em um piso sem atrito. Em quais dessas situações a aceleração do objeto possui:
(a) uma componente ?
(b) uma componente ?
(c) Em cada situação, indique o sentido de indicando um quadrante ou um sentido ao longo de um eixo. (Isso pode ser feito com alguns cálculos mentais.)
Questão 2
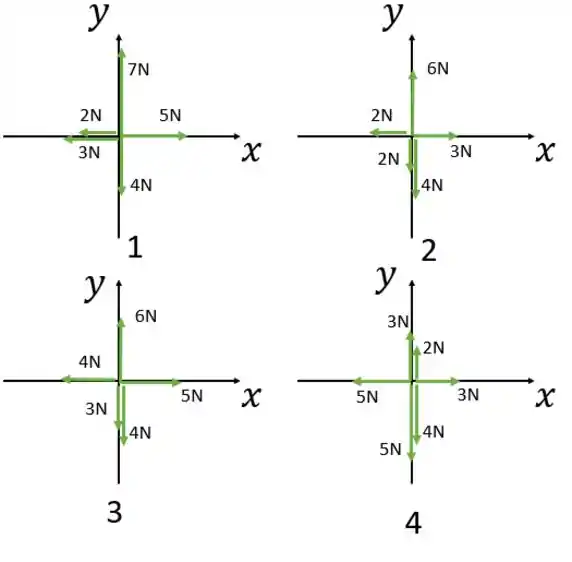
Duas forças horizontais e agem sobre um disco de que desliza sem atrito sobre o gelo, no qual foi desenhado um sistema de coordenadas . A força aponta no sentido positivo do eixo e tem módulo de . A força tem um módulo de . A Fig. 5-34 mostra a componente da velocidade do disco em função do tempo . Qual é o ângulo entre as orientações constantes das forças e ?
Questão 3
Uma partícula de se move ao longo de um eixo de acordo com a equação , com em metros e em segundos. Qual é, na notação dos vetores unitários, a força que age sobre a partícula no instante ?
Ver solução completaQuestão 4
Uma partícula de se move ao longo de um eixo sob a ação de uma força variável. A posição da partícula é dada por , com em metros e em segundos. O fator é constante. No instante , a força que age sobre a partícula tem um módulo de e aponta no sentido negativo do eixo x. Qual é o valor de ?
Ver solução completaQuestão 5
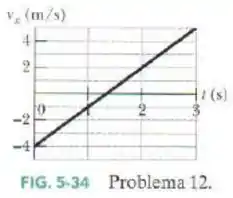
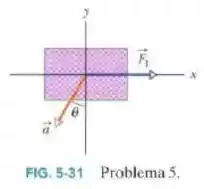
Duas forças agem sobre a caixa de vista de cima na Fig.5-31, mas apenas uma é mostrada. Para , e , determine a segunda força (a) em termos dos vetores unitários e como um (b) módulo e (c) um ângulo em relação ao semieixo positivo.
Questão 6
Sobre um corpo, de massa , atuam três forças, , e . Duas delas, mostradas na figura abaixo à esquerda, tem módulos iguais a , mas atuam em direções diferentes. O corpo está inicialmente em repouso sobre uma mesa horizontal sem atrito. Na figura da direita, é mostrado um gráfico da velocidade escalar do corpo em função do tempo, onde cada quadrado na vertical equivale a . Considere e .
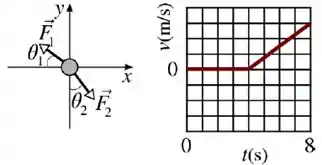
No intervalo entre e sabe-se que o copo se desloca em uma trajetória retilínea no sentido positivo do eixo . Neste intervalo de tempo a força é dada por:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 7
Um elétron com penetra horizontalmente em uma região onde está sujeito a uma força vertical constante de . A massa do elétron é . Determine a deflexão vertical sofrida pelo elétron enquanto percorre uma distância horizontal de
Ver solução completaQuestão 8
Um corpo de massa parte do repouso e após sua velocidade é de . Considerando que o corpo foi submetido a uma força externa constante, responda:
Qual é o módulo da força externa?
a)
b)
c)
d)
e)
Ver solução completaQuestão 10
Dois discos de massas e estão ligados por uma mola ideal comprimida sobre uma mesa horizontal lisa. Em um dado instante a força da mola sobre o primeiro disco é e uma força paralela ao plano da mesa está aplicada sobre o segundo disco, como mostra a figura (mesa vista de cima). No instante considerado a aceleração do centro de massa do sistema constituído pelos discos e pela mola é
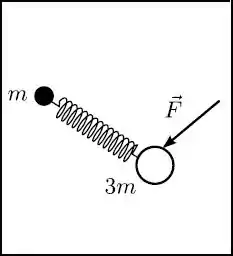
- ;
- ;
- ;
- ;
- ;
Questão 14
Um objeto sofre um deslocamento sob a ação de uma força constante que aponta para o norte. O trabalho realizado pela força é positivo. Qual das afirmações é necessariamente verdadeira sobre a velocidade média do objeto durante o deslocamento?
(A) A velocidade média é zero.
(B) A velocidade média aponta para o norte.
(C) A velocidade média aponta para o sul.
(D) A velocidade média tem uma componente na direção norte.
(E) A velocidade média tem uma componente na direção sul.
Ver solução completaQuestão 17
Considere o sistema da figura ao lado. A corda e a polia possuem massas desprezíveis, a corda é inextensível e a polia não possui atrito em seu eixo. O coeficiente de atrito cinético entre o bloco de massa M e o topo da mesa é . Os blocos são liberados a partir do repouso e começam a se acelerar. Dê respostas em termos de e .
2) justifique porque a tensão dos dois lados da corda e nas bordas da polia têm o mesmo valor,

Questão 18
Considere o sistema da figura ao lado. A corda e a polia possuem massas desprezíveis, a corda é inextensível e a polia não possui atrito em seu eixo. O coeficiente de atrito cinético entre o bloco de massa M e o topo da mesa é . Os blocos são liberados a partir do repouso e começam a se acelerar. Dê respostas em termos de e .
5) a velocidade dos blocos depois de terem se movido uma distância

Questão 19
A figura mostra uma partícula em movimento circular uniforme que se desloca no sentido anti-horário. As setas enumeradas de 1 a 5 representam a direção de vetores associados a grandezas físicas da dinâmica desta partícula (medidas a partir de um referencial inercial em repouso em relação à trajetória da partícula). Dentre as alternativas a abaixo, assinale aquela que associa corretamente as setas às grandezas físicas descritas, quando a partícula está na posição indicada na figura.
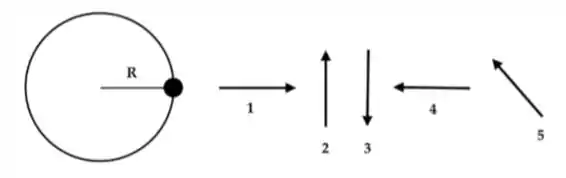
(a) Setas 3 e 4 para a força resultante e velocidade, respectivamente.
(b) Setas 1 e 2 para a força resultante e velocidade, respectivamente.
(c) Setas 1 e 4 para a força resultante e aceleração, respectivamente.
(d) Setas 4 e 2 para a força resultante e velocidade, respectivamente.
(e) Setas 4 e 5 para a força resultante e velocidade, respectivamente.
Ver solução completaQuestão 21
A resultante das três únicas forças que agem sobre uma partícula é nula. Assinale a afirmativa correta.
(a) Não é possível três forças se anularem.
(b) As três forças têm necessariamente o mesmo módulo.
(c) O módulo de uma força é necessariamente igual a soma dos módulos das outras duas.
(d) As três forças têm necessariamente a mesma direção
(e) Nenhuma das demais respostas está correta.
Ver solução completaQuestão 22
Um corpo de massa parte do repouso e após sua velocidade é de . Considerando que o corpo foi submetido a uma força externa constante, responda:
Qual é o módulo da força externa?
a)
b)
c)
d)
e)
Ver solução completaQuestão 23
Um bloco de gelo com massa de está inicialmente em repouso sobre uma superfície horizontal sem atrito. A seguir, um trabalhador aplica uma força horizontal sobre ele. Como resultado, o bloco se move ao longo do eixo de tal modo que sua posição em função do tempo é dada por , onde e .
b) Calcule o módulo de quando .
Ver solução completaQuestão 24
2 – Duas partículas partem da origem, a primeira de massa com velocidade caracterizada por e a segunda, de massa e com velocidade .
As velocidades são relativas ao mesmo observador na origem. Determine:
a) Como o vetor centro de massa do sistema varia com o tempo?
b) em que ponto do espaço estará o centro de massa em ?
c) Neste instante, , qual é o vetor velocidade instantânea do centro de massa do sistema?
d) Qual o vetor força externa que atua sobre este sistema de partículas?
Ver solução completaQuestão 25
Um avião sobe com rapidez constante de 240 m/s ao longo de uma linha reta inclinada de 24° em relação à horizontal. Qual das afirmações abaixo é verdadeira a respeito do módulo da força resultante sobre o avião?
A) É igual a zero.
B) É igual ao peso do avião.
C) É igual ao módulo da força de resistência do ar.
D) É menor do que o peso do avião mas é maior que zero.
E) É igual à componente do peso do avião na direção do movimento.
Ver solução completaQuestão 27
(Capítulo 5.9 – Exercício 25) Qual é o módulo da força necessária para acelerar um trenó-foguete de até em , partindo do repouso?
Ver solução completaQuestão 28
(Cap 5 – Ex 1) Se um corpo padrão de tem uma aceleração de a com o semi-eixo positivo, quais são
(a) a componente e
(b) a componente da força resultante a que o corpo está submetido e
(c) qual é a força resultante em termos dos vetores unitários?
Ver solução completaQuestão 29
Um bloco, inicialmente em repouso, se desloca sob ação de uma força de (atuante por 10 segundos) sem força de atrito. Durante a ação dessa força foi adquirida uma aceleração de . Qual é a massa desse bloco?
- 15 kg
- 10 kg
- 25 kg
- 5 kg
- 20 kg
Questão 30
Sobre um corpo de massa atuam simultaneamente as forças , e .
Se no instante o corpo se encontra em repouso, a velocidade do corpo é dada por:
Questão 31
Um ginasta de massa sobe em uma corda vertical que está presa ao teto e cuja massa é desprezível. Quais das alternativas abaixo são verdadeiras?
(I) quando o ginasta se dependura de maneira estática na corda, a única força que age sobre ele é o peso.
(II) quando o ginasta sobe pela corda com velocidade constante, a tensão na corda é maior que o peso.
(III) quando o ginasta sobe de maneira acelerada, a tensão na corda é maior que o peso.
(IV) quando o ginasta desce de maneira acelerada, a tensão na corda é menor que o peso.
(a) I e III.
(b) II apenas.
(c) III e IV.
(d) I apenas.
(e) I e II.
Ver solução completaQuestão 32
O vetor posição (em metros) de uma partícula em função do tempo (em segundos) é dado por:
Se a partícula tem , determine a força resultante agindo sobre ela no instante .
Questão 33
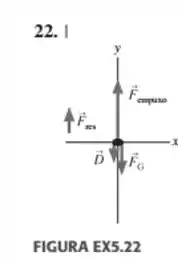
Uma corrente com quatro elos ( cada) é puxada para cima por uma força vertical (assinalada na figura abaixo) de módulo igual a .

Desenhe um diagrama das forças que atuam sobre cada elo.
Escolha um sistema de referência e escreva as forças nesse referencial.
Escreva as leis de Newton para o problema e deduza as equações pertinentes.
Calcule a aceleração da corrente.
Calcule as forças que atuam nos elos.
Ver solução completaQuestão 34
Um pintor de está sobre uma plataforma de suspensa por uma roldana ideal (veja a figura abaixo). Puxando a corda ele faz a plataforma subir com aceleração de .
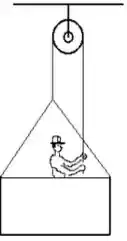
Desenhe o diagrama de forças que atuam no pintor e na plataforma e escolha um sistema de referência.
Escreva as leis de Newton para o pintor e para a plataforma.
Determine cada uma das forças que atuam no pintor.
Determine cada uma das forças que atuam na plataforma.
Ver solução completaQuestão 35
Enunciado das questões (Q6) e (Q7).
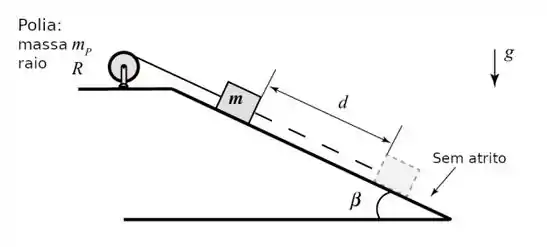
Um cilindro uniforme de massa e raio está apoiado num eixo horizontal, podendo girar livremente, sem atrito. Uma corda enrolada no cilindro prende um bloco de massa , que pode deslizar sem atrito sobre um plano inclinado de ângulo , como mostra a figura. O sistema é solto, a partir do repouso, quando está a uma altura acima da horizontal.
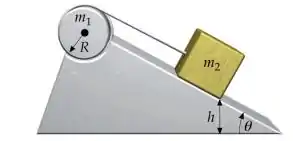
(Q6) [1,0 ponto] Considerando que a corda não desliza sobre o cilindro, a aceleração de é:
Questão 36
Um carro está fazendo uma curva apoiado em um plano inclinado da forma indicada na figura ao lado, que mostra o plano transversal ao movimento do carro.
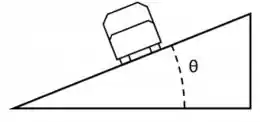
- Faça um esboço das forças que atuam no carro no plano transversal ao movimento. Considere que o atrito é desprezível.
- Desprezando o atrito, encontre a velocidade com a qual o carro está fazendo a curva em função da aceleração da gravidade , do raio de curvatura desta curva, , e do ângulo de inclinação da curva, .
- Deste item em diante, considere agora uma situação em que há atrito e o motorista está correndo na velocidade máxima sem escorregar para fora da curva. Esboce as forças envolvidas no plano transversal nesta situação.
- Encontre a velocidade máxima na qual o carro ainda é capaz de fazer a curva sem derrapar em função de , , e o coeficiente de atrito estático .
Questão 37
Enunciado das questões (Q6) e (Q7).
Um cilindro uniforme de massa e raio está apoiado num eixo horizontal, podendo girar livremente, sem atrito. Uma corda enrolada no cilindro prende um bloco de massa , que pode deslizar sem atrito sobre um plano inclinado de ângulo , como mostra a figura. O sistema é solto, a partir do repouso, quando está a uma altura acima da horizontal.
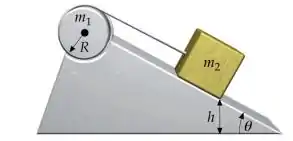
(Q6) [1,0 ponto] A velocidade v com que chega ao plano horizontal é:
Questão 38
Q - Durante o intervalo de tempo de a , uma partícula de massa experimenta uma mudança na sua velocidade de a , respectivamente, como consequência da ação da força resultante constante . Podemos afirmar que o valor do módulo da força , medido em Newtons, que
age na partícula, é:
Ver solução completaQuestão 39
Q - Uma partícula de massa (medida em ) se movimenta sob a ação da força resultante (medida em Newtons). Se em a partícula está localizada em (medido em metros) e tem velocidade (medida em ), determine o módulo do vetor posição da partícula (medido em metros) em um instante (medido em segundos).
Ver solução completaQuestão 40
Um fio ideal tem uma de suas extremidades presa no teto e passa por duas polias também ideais. Uma lata com uma massa está pendurada em uma das polias (por um fio também ideal) e uma força de módulo desconhecido é aplicada por uma pessoa na extremidade livre do fio de maneira que a lata sobe com velocidade constante. A situação está representada na figura ao lado.
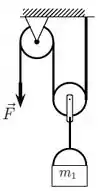
(c) Qual o módulo da força ? Só serão consideradas respostas justificadas.
Ver solução completaQuestão 41
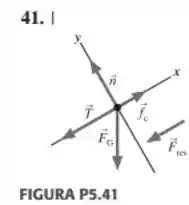
[Enunciado comum às Questões 5 e 6]
Sobre um corpo, de massa , atuam três forças, , e . Duas delas, mostradas na figura abaixo à esquerda, tem módulos iguais a , mas atuam em direções diferentes. O corpo está inicialmente em repouso sobre uma mesa horizontal sem atrito. Na figura da direita, é mostrado um gráfico da velocidade escalar do corpo em função do tempo, onde cada quadrado na vertical equivale a . Considere e .
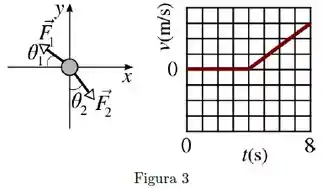
[Questão 6]
No intervalo entre e sabe-se que o copo se desloca em uma trajetória retilínea no sentido positivo do eixo . Neste intervalo de tempo a força é dada por:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 42
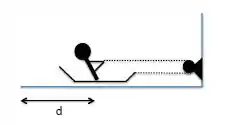
Considere um sistema formado por uma pessoa e um trenó, com massa total , inicialmente em repouso. A pessoa presa ao trenó puxa uma corda ideal com uma força horizontal, constante e de módulo . A corda passa por uma roldana de massa desprezível e está ligada ao trenó, conforme a figura. Considere que o trenó está sobre uma superfície horizontal cujo atrito é desprezível.
a) Desenhe o diagrama de forças que atuam sobre o sistema pessoa + trenó, enquanto a pessoa está puxando a corda;
b) Calcule o tempo necessário que o sistema leva para percorrer uma distância a partir do repouso.
Questão 43
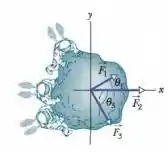
Três astronautas, impulsionados por mochilas a jato, empurram e guiam um asteroide de para uma base de manutenção, exercendo as forças mostradas na Fig. 5-29, com , , , e . Determine a aceleração do asteroide
(a) em termos dos vetores unitários e como
(b) um módulo e
(c) um ângulo em relação ao semieixo positivo.
Questão 44
Uma partícula, inicialmente está em repouso, passa a estar sob a ação de três forças de mesmo módulo . Duas são perpendiculares entre si e a terceira faz um ângulo com uma delas, conforme mostrado na figura.
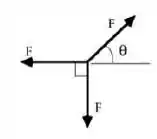
Qual a única verdadeira das seguinte afirmativas:
- Essa partícula não permanecerá em repouso.
- A partícula permanecerá em repouso, independente do ângulo e do módulo de , pois as forças se anulam.
- A partícula permanecerá em repouso somente se o ângulo for .
- A partícula pode permanecer em repouso ou não, dependendo do módulo da força .
Questão 45
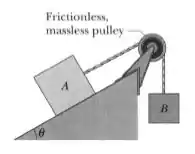
Na figura abaixo dois blocos estão conectados por um fio que passa por uma polia. A massa do bloco é e o coeficiente de atrito cinético entre e a rampa é . O ângulo da rampa é . O bloco desliza para baixo ao longo da rampa com velocidade constante. Qual é a massa do bloco ?
Questão 46
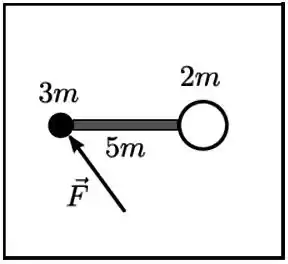
Dois discos de massas e estão ligados por uma barra rígida de massa sobre uma mesa horizontal lisa. Uma força paralela ao plano da mesa está aplicada sobre o primeiro disco em um certo instante, como mostra a figura (da mesa vista de cima). Nesse instante, a aceleração do centro de massa do sistema constituído pelos discos e pela barra
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 47
Parte III - Um corpo de massa está submetido à ação de três forças dadas por:
- Encontre a aceleração desse corpo.
- Sabe-se que a velocidade inicial do citado corpo era . Encontre a velocidade após .
Questão 48
Na figura ao lado um bloco de massa desliza sobre um plano horizontal com coeficiente de atrito cinético . Ele está ligado por uma corda ideal, que passa por uma polia (disco uniforme de raio e massa ), a um outro bloco de massa que está suspenso. Considere que a corda não escorrega na polia, e que não há atrito no eixo da polia. O sistema é solto do repouso em e as massas entram em movimento.
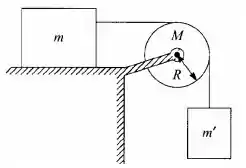
a) Encontre a aceleração linear dos blocos, a aceleração angular da polia, e as trações nos dois lados da corda. A aceleração angular é positiva ou negativa nesse caso?
Ver solução completaQuestão 49
Dois blocos homogêneos e em forma de paralelepípedo, de massas e estão apoiados num piso e formam um sistema conforme a figura ao lado. Por meio de um cordão, deseja-se puxar e imprimir um movimento retilíneo uniformemente acelerado ao sistema, inicialmente em repouso. Considerando que o coeficiente de atrito cinético entre a superfície de B e a do piso vale ; que entre as superfícies de A e de B vale ; que e que o operador puxa o bloco B com uma força , calcule:
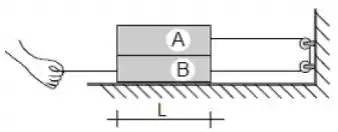
c) Depois de quanto tempo o centro do bloco A ficará alinhado verticalmente com a extremidade do bloco B?
Ver solução completaQuestão 50
Dois blocos homogêneos e em forma de paralelepípedo, de massas e estão apoiados num piso e formam um sistema conforme a figura ao lado. Por meio de um cordão, deseja-se puxar e imprimir um movimento retilíneo uniformemente acelerado ao sistema, inicialmente em repouso. Considerando que o coeficiente de atrito cinético entre a superfície de B e a do piso vale ; que entre as superfícies de A e de B vale ; que e que o operador puxa o bloco B com uma força , calcule:
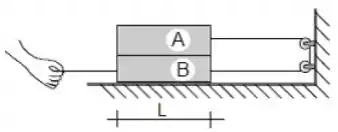
a) A aceleração dos blocos.
Ver solução completaQuestão 51
Considere o sistema da figura ao lado. A corda e a polia possuem massas desprezíveis, a corda é inextensível e a polia não possui atrito em seu eixo. O coeficiente de atrito cinético entre o bloco de massa M e o topo da mesa é . Os blocos são liberados a partir do repouso e começam a se acelerar. Dê respostas em termos de e .
- Faça o diagrama de forças para os dois blocos, para as duas partes da corda e para a roldana e identifique os pares de ação e reação

Questão 52
O vetor representa a posição em metros de uma partícula de massa . Qual a força resultante que atua sobre a partícula no
tempo ?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
(i)
Ver solução completaQuestão 53
Somente duas forças, uma de módulo 3 N e outra de módulo 5 N, são aplicadas a um objeto. Para qual das orientações das forças mostradas nos diagramas abaixo o módulo da aceleração do objeto será mínimo?
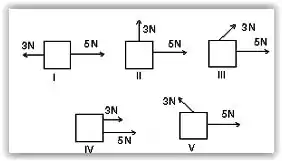
A) I
B) II
C) III
D) IV
E) V
Ver solução completaQuestão 54
Sobre um objeto que se move com velocidade constante em um referencial inercial, sabemos necessariamente que:
(A) Há no mínimo duas forças atuando sobre ele.
(B) Ele acabará parando devido à inércia.
(C) Não há força da gravidade atuando sobre ele.
(D) Pode haver forças atuando sobre ele, desde que a resultante seja nula.
(E) Não há nenhuma força de atrito atuando sobre ele.
Ver solução completaQuestão 55
Em qual dos exemplos abaixo a segunda lei de Newton na forma não é válida?
(a) Movimento da lua em torno da Terra;
(b) Queda livre de um objeto sólido;
(c) Movimento de rotação da terra em torno do seu eixo;
(d) Lançamento de um foguete;
(e) Movimento oscilatório de um pêndulo;
Ver solução completaQuestão 56
Uma força é aplicada a um bloco de que desliza sobre um superfície onde o coeficiente de atrito dinâmico é 0. O corpo tem aceleração constante de . Qual a força aplicada no corpo?
(a)
(b)
(c) ;
(d) ;
(e) ;
Ver solução completaQuestão 57
(G1 - CFTMG 2012) Na figura, os blocos e , com massas iguais a e , respectivamente, são ligados por meio de um cordão inextensível.
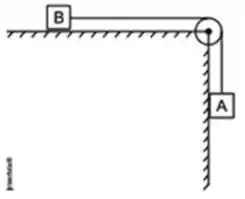
Desprezando-se as massas do cordão e da roldana e qualquer tipo de atrito, aaceleração do bloco , em é igual a quanto?
- 3
- 2
- 5
- 1
- 4
Questão 58
A figura mostra um aparato construído para experimentos em escolas, no qual a superfície de apoio é perfeitamente lisa e o fio e a polia são ideais. Neste aparato, são colocados um bloco de concreto de massa apoiado sobre a superfície horizontal e outro bloco de preso ao fio. Podemos afirmar, então, que a aceleração adquirida pelo conjunto, em , vale:
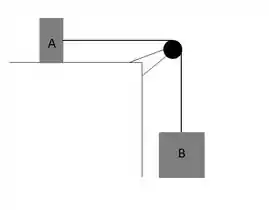
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 59
Um bloco de massa , move-se com velocidade constante de num plano horizontal, sob a ação da força , constante e horizontal. Se o coeficiente de atrito entre o bloco e o plano vale , e a aceleração da gravidade, , então o módulo da força , em Newtons, vale:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 60
Considere as seguintes afirmações:
I. Um corpo sob a ação de uma força , se move sempre na direção e sentido desta força.
II. No movimento retilíneo uniformemente variado a aceleração tem sempre o mesmo sentido da velocidade.
III. O vetor posição de um corpo num instante t qualquer é dado por, , onde é o vetor posição inicial, é o vetor velocidade inicial e o vetor aceleração onde todos são vetores constantes em módulo direção e sentido, neste caso a trajetória do corpo é necessariamente parabólica.
Das afirmativas acima quais (ou qual) estão incorretas:
a) Todas as afirmativas.
b) Apenas I
c) Apenas II
d) Apenas III
e) Apenas I e II
f) Apenas I e III
g) Apenas II e III
h) Nenhuma das afirmativas.
Ver solução completaQuestão 61
14 - Sobre uma pista horizontal de atrito desprezível, estão deslizando os corpos e com aceleração provocada pela força horizontal de intensidade , aplicada no corpo . Sabendo- se que a massa de é o dobro da massa de , a força que o corpo exerce no corpotem intensidade de:
A)
B)
C)
D)
E)

Questão 62
Um carro leve puxa uma caminhonete mais pesada utilizando um cabo ideal. Após um certo intervalo de tempo, eles se movem ao longo da estrada de maneira que a distância relativa entre eles é constante e com aceleração constante no sentido do movimento. Quais das afirmativas abaixo são verdadeiras?
(I) a força resultante no carro é igual à resultante que atua na caminhonete.
(II) a força resultante no carro é maior que a resultante que atua na caminhonete.
(III) a força resultante no carro é menor que a resultante que atua na caminhonete.
(IV) a força que o carro exerce no cabo tem módulo maior ou igual ao da força exercida pela caminhonete sobre o cabo.
(V) a força que o carro exerce no cabo tem módulo menor que o da força exercida pela caminhonete sobre o cabo.
(a) I e IV.
(b) I e V.
(c) II e IV.
(d) II e V.
(e) III e IV.
Ver solução completaQuestão 63
Uma partícula cuja massa é está sujeita à duas forças e simultaneamente, onde e estão em . Encontre o módulo da aceleração resultante e o ângulo que ela faz com o eixo positivo.
a) e
b) e
c) e
d) e
Ver solução completaQuestão 64
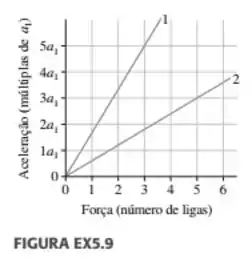
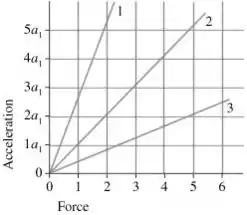
7 - A figura mostra um gráfico de aceleração versus força para três objetos puxados por cordas ideais. A massa do objeto 2 é de . Quais são as massas dos objetos 1 e 3, respectivamente?
A) 14kg e 90kg
B) 72kg e 18kg
C) 90kg e 18kg
D) 14kg e 72kg
E) 14kg e 18Kg
Questão 65
No estudo da mecânica, as palavras “cinemática” e “dinâmica” referem-se, respectivamente, a:
a. As duas palavras tem o mesmo significado.
b. A cinemática nos diz o porquê de determinado movimento e a dinâmica nos diz como este movimento ocorre
c. A cinemática nos diz como determinado movimento ocorre e a dinâmica nos diz o porquê deste movimento
d. A cinemática é o estudo de objetos parados e a dinâmica é o estudo de objetos em movimento.
e. Nenhuma das anteriores
Ver solução completaQuestão 66
Dois blocos conectados por uma corda passando por uma pequena polia, sem atrito, e em repouso num plano também sem atrito (veja a figura abaixo).
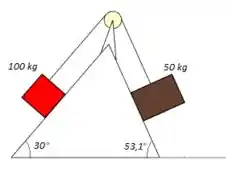
(b) Qual a aceleração dos blocos?
Ver solução completaQuestão 67
O vetor velocidade (em ) de uma partícula é , onde e são os vetores unitários ao longo dos eixos e , respectivamente. Se a partícula tem massa , qual é a força resultante agindo sobre ela (em Newtons)?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 68
Um pêndulo simples é mantido em repouso indicada através de aplicação de uma força de módulo que faz um ângulo de com o fio de massa desprezível. O ângulo entre o fio e a vertical é , como mostra a figura.
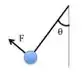
Qual a relação entre o módulo da força e o módulo da força de tração do fio sobre a bolinha ? Considere .
Escolha uma:
Não é possível calcular a relação sem conhecer a massa da bolinha.
Nenhuma das outras alternativas está correta.
Ver solução completaQuestão 69
Uma bola de rola de um balcão de cozinha e pousa a de distância de sua base. Uma bola de rola do mesmo balcão com a mesma velocidade. Ela pousa a ................ da base do balcão.
menos de
mais de
Ver solução completaQuestão 70
Um carro com tração dianteira percorre uma estrada que apresenta coeficiente de atrito igual a entre os pneus do carro e a própria estrada. Neste carro, tem-se uma distribuição de peso equivalente a do peso (carro + passageiros) nas rodas traseiras e do peso nas rodas dianteiras. Sabendo-se que , calcule a máxima aceleração que o carro pode atingir.
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 72
Uma caixa de massa está sobre outra caixa, de massa , tal que . Uma pessoa tenta arrastar as caixas, puxando a de cima com uma força de módulo F, que faz um ângulo com a horizontal, conforme a figura abaixo.
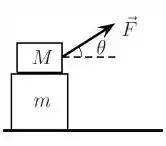
Sabe-se que o atrito entre a caixa de baixo e o chão pode ser desprezado e que o coeficiente de atrito estático entre as duas caixas é . Observa-se que o sistema composto pelas duas caixas se desloca em conjunto.
(a) Isole as caixas e faça um diagrama indicando as forças que atuam sobre cada uma
delas.
(b) Qual a aceleração das caixas?
(c) Qual o menor valor que pode ter para que o sistema continue a se movimentar em
conjunto?
Ver solução completaQuestão 73
(Cap 4 – Ex 41) Um objeto de 4,0 kg é submetido a duas forças constantes, e . O objeto está em repouso na origem no tempo (a) Qual é a aceleração do objeto?
(b) Qual é a sua velocidade no tempo ?
(c) Onde está o objeto no tempo ?
Ver solução completaQuestão 74
Um elétron de massa e velocidade horizontal incide em uma região entre duas placas paralelas eletricamente carregadas, conforme mostra a figura abaixo. Ao percorrer essa região o elétron é submetido a uma forca vertical , constante, para cima. Sabendo-se que o comprimento das placas é igual a e desprezando o efeito da aceleração da gravidade, determine:
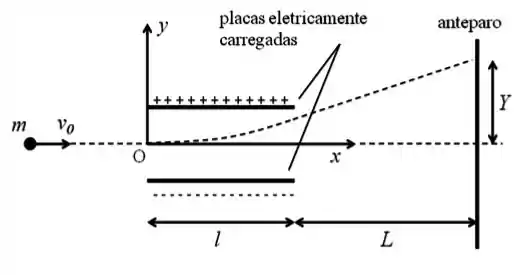
O vetor posição do elétron em função do tempo, quando este se encontra entre as placas paralelas eletricamente carregadas. Considere que a origem do sistema de coordenadas é do lado esquerdo das placas e que o elétron passa pela origem do sistema de coordenadas no instante , conforme mostra a figura. Expresse o resultado em termos de , , , e .
O valor de , quando o elétron atinge um anteparo situado a uma distancia das placas paralelas. Expresse o resultado em termos de , , , , .
Ver solução completaQuestão 75
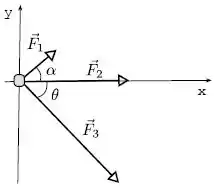
Uma partícula de massa encontra-se sob a ação de três forças constantes, como mostra a figura abaixo. Os módulos das forças são , e . Os ângulos da figura são tais que , , e . Determine o vetor aceleração da partícula.
Questão 76
Um elevador se move para cima com aceleração constante. A curva pontilhada mostra a posição do teto do elevador em função do tempo . No instante indicado na figura, uma lâmpada se solta do teto e cai. Na figura abaixo, qual das curvas contínuas melhor representa a trajetória da lâmpada em função do tempo?
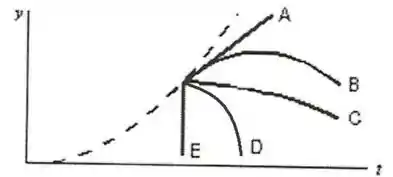
Questão 77
A velocidade de uma partícula em movimento linear depende da posição de acordo com a equação
sendo uma constante positiva. Encontre a força que atua na partícula em função de . (sugestão: utilize a equação fundamental da dinâmica na forma )
Ver solução completaQuestão 78
Encontre a velocidade em função do tempo no item e em função de no item para uma partícula de massa . Em ambos os casos, a partícula está partindo do repouso em em .
Onde e são constantes positivas reais.
Ver solução completaQuestão 79
Encontre o comportamento assintótico da velocidade para os casos e .
Onde e são constantes positivas reais.
Ver solução completaQuestão 80
Uma força de módulo é exercida no lado esquerdo da face de dois blocos que estão colocados lado-à-lado em uma superfície sem atrito, com as duas faces se tocando. A inércia do bloco da direita é e a do bloco da esquerda é .
a) Desenhe o diagrama de corpo livre dos blocos e calcule o módulo da aceleração de cada bloco. b) Qual o módulo e sentido da força de contato que o bloco da esquerda exerce no bloco da direita?
c) Qual o módulo e sentido da força de contato que o bloco da direita exerce no bloco da esquerda?
d) Como suas respostas se alteram nas partes a), b) e c) se a posição dos dois blocos é invertida?
Ver solução completaQuestão 81
Um fio ideal tem uma de suas extremidades presa no teto e passa por duas polias também ideais. Uma lata com uma massa está pendurada em uma das polias (por um fio também ideal) e uma força de módulo desconhecido é aplicada por uma pessoa na extremidade livre do fio de maneira que a lata sobe com velocidade constante. A situação está representada na figura ao lado.
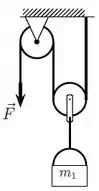
(a) Faça um diagrama indicando as forças que atuam sobre a lata e sobre as polias.
Ver solução completaQuestão 82
Duas forças () agem sobre uma caixa de massa que desliza livremente sobre uma superfície plana. Na figura, temos uma vista de cima da situação, mas apenas uma força é mostrada além do vetor aceleração da caixa. Considerando que o módulo da força , a aceleração da caixa tem módulo igual a e o ângulo , a única afirmação incorreta é:
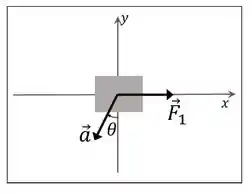
(a) O módulo da componente horizontal da força é maior do que o módulo da componente horizontal da força .
(b) O módulo da força resultante é igual a .
(c) A componente vertical da força resultante possui o mesmo módulo que a componente vertical da força
(d) O módulo da força é maior que o módulo da força resultante
(e) O módulo da componente horizontal da força é menor do que o módulo da componente horizontal da força .
Ver solução completaQuestão 83
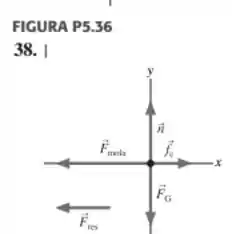
Um bloco move-se sobre uma superfície horizontal com atrito. As forças que agem sobre o bloco estão indicadas no diagrama, a força faz um ângulo com a horizontal.
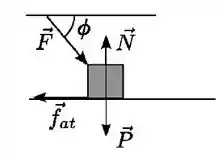
Se o bloco se move com velocidade constante, podemos afirmar que:
(a)
(b)
(c)
(d)
(e) Nada podemos afirmar porque não conhecemos o coeficiente de atrito
Ver solução completaQuestão 84
Dois blocos conectados por uma corda passando por uma pequena polia, sem atrito, e em repouso num plano também sem atrito (veja a figura abaixo).
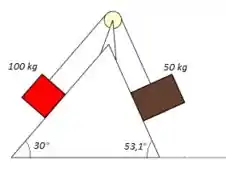
(c) Qual a tensão da corda?
Ver solução completaQuestão 85
(Cap 5 – Ex 3) Apenas duas forças horizontais atuam em um corpo de que pode se mover em um piso sem atrito. Uma força é de e aponta para o leste; a outra é de e atua ao norte do oeste. Qual é o módulo da aceleração do corpo?
Ver solução completaQuestão 86
(Cap 5 – Ex 7) Três astronautas, impulsionados por mochilas a jato, empurram e guiam um asteroide de para uma base de manutenção, exercendo as forças mostradas na Fig. 5-29, com , , , e . Determine a aceleração do asteroide
(a) em termos dos vetores unitários e como
(b) um módulo e
(c) um ângulo em relação ao semi-eixo positivo.
Ver solução completaQuestão 87
Um objeto de massa parte do repouso e, atuado por uma força constante , atinge a velocidade de depois de . Então o valor da força é:
A. .
B.
C.
D.
E.
Ver solução completaQuestão 88
Um objeto move-se com velocidade constante relativamente a um sistema de referência inercial. Qual das afirmações abaixo é necessariamente verdadeira?
A) Não há forças agindo sobre o objeto.
B) Uma pequena força age sobre o objeto, na direção do movimento.
C) A força resultante sobre o objeto é zero.
D) Duas das afirmações anteriores são necessariamente verdadeiras.
E) Todas as afirmações anteriores são falsas.
Ver solução completaQuestão 89
Um balão se desloca horizontalmente no ar com rapidez constante. Em dado instante uma pedra cai do balão, permanece no ar durante e atinge o solo segundo uma direção que faz um ângulo de com a vertical, como na figura abaixo. Desprezando-se a resistência do ar, responda:
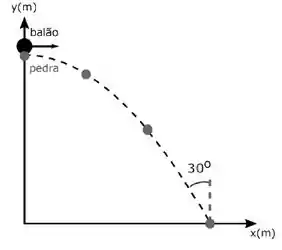
É correto afirmar que:
(A) As acelerações do balão e da pedra apontam verticalmente para baixo.
(B) No instante em que a pedra cai do balão, a aceleração da pedra é paralela à sua velocidade.
(C) O tempo de queda da pedra depende da aceleração e da rapidez do balão.
(D) Durante todo o movimento a aceleração do balão é nula, enquanto a da pedra aponta verticalmente para baixo.
(E) A aceleração da pedra é paralela à sua velocidade no instante imediatamente antes de sua colisão com o solo.
Ver solução completaQuestão 91
Um plano inclinado de massa M repousa em uma mesa horizontal sem atrito. Um bloco de massa m é colocado sobre esse plano (figura abaixo). Não existe atrito entre o bloco e o plano. O sistema é liberado do repouso.
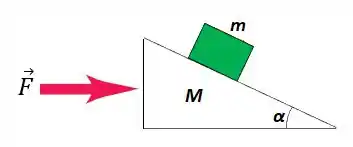
(a) Calcule a aceleração do plano e as componentes horizontal e vertical de aceleração do bloco.
Ver solução completaQuestão 92
Um plano inclinado de massa M repousa em uma mesa horizontal sem atrito. Um bloco de massa m é colocado sobre esse plano (figura abaixo). Não existe atrito entre o bloco e o plano. O sistema é liberado do repouso.
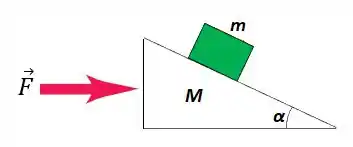
(b) Sua resposta da parte (a) se aproxima do resultado correto quando é muito grande?
Ver solução completaQuestão 93
8) Considere a situação mostrada na figura ao lado. Não há atrito entre os blocos e a superfície horizontal. Se , qual é o módulo da força Exercida pelo bloco 2 sobre o bloco 1?
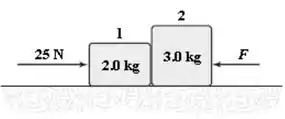
a)
b)
c)
d)
e)
Ver solução completaQuestão 94
Uma esfera uniforme de raio e massa gira com velocidade angular inicial em torno do eixo horizontal que passa pelo seu centro, conforme figura ao lado (eixo saindo do papel). Ela é então colocada, no instante , suavemente sobre um piso cujo coeficiente de atrito cinético com a bola é . Note que no instante inicial em que ela é colocada no piso, ela só possui rotação, sem translação (ela está inicialmente só patinando).
a) Logo após ser colocada no piso, desenhe as forças que atuam na bola, identificando os pontos em que elas são aplicadas.
Ver solução completaQuestão 95
Uma pessoa permanece de pé numa subida com inclinação de um ângulo com respeito a horizontal. As pernas da pessoa estão separadas entre si por uma distância com um pé na frente do outro. O centro de massa da pessoa está a uma altura do chão, perpendicular a superfície da subida, e no meio das pernas da pessoa. Assuma que o coeficiente de atrito estático entre os pés da pessoa e a subida é grande o suficiente para a pessoa não deslizar.
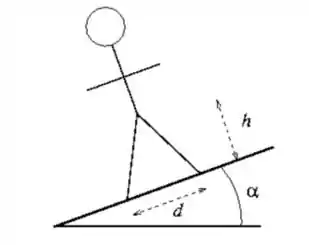
Quais são as magnitudes das forças normais em cada pé? Elas são diferentes para cada pé.
Expresse suas respostas em termos das variáveis do problema
Ver solução completaQuestão 96
Uma pessoa permanece de pé numa subida com inclinação de um ângulo com respeito a horizontal. As pernas da pessoa estão separadas entre si por uma distância com um pé na frente do outro. O centro de massa da pessoa está a uma altura do chão, perpendicular a superfície da subida, e no meio das pernas da pessoa. Assuma que o coeficiente de atrito estático entre os pés da pessoa e a subida é grande o suficiente para a pessoa não deslizar.
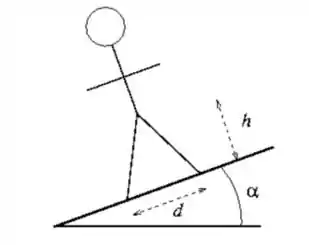
Quanto os pés devem estar separados para que a força normal no pé da frente seja zero? Esta é a situação em que a pessoa começa a rotacionar e cair de costas.
Expresse suas respostas em termos das variáveis do problema.
Ver solução completaQuestão 97
Uma haste uniforme de comprimento e massa está presa num muro por uma de suas extremidades. Na outra extremidade, está amarrado um cabo que é ligado ao muro. O cabo faz um ângulo com a haste. Assuma que o cabo tenha massa desprezível, mas existe forças de contato nele.
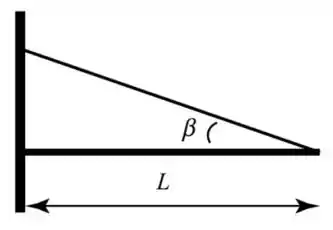
- Qual é a magnitude da tensão no cabo?
- Qual o ângulo da força de contato entre a haste e o muro?
- Qual a magnitude da força de contato entre a haste e o muro?
Questão 98
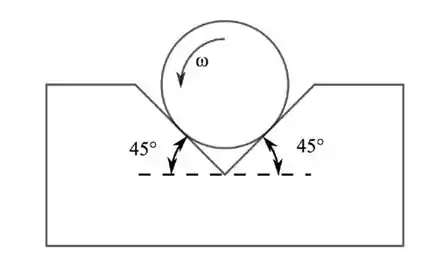
Um cilindro de massa e raio está rodando sobre uma fenda em com uma velocidade angular . O coeficiente de atrito entre o cilindro e a superfície é .
Qual é o torque externo necessário aplicado no cilindro para que ele se mantenha rotacionando com velocidade constante?
Expresse suas respostas em termos das variáveis do exercício e considere para a aceleração da gravidade.
Questão 99
Considere uma polia de massa com raio que tem momento de inércia igual a . A polia é livre para rodar em torno de um eixo central sem atrito. Uma corda sem massa é amarrada por uma extremidade na polia e na outra extremidade é atada a um bloco de massa , que está em repouso sobre um plano inclinado de ângulo com respeito a horizontal. A magnitude da aceleração da gravidade é . Então, permite-se que o bloco deslize. Quanto tempo leva para o bloco andar de uma distância no plano inclinado? Escreva sua resposta usando as variáveis do exercício.
Questão 100
Questão 10
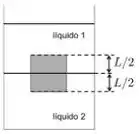
É constatado que um determinado corpo homogêneo de forma cúbica está em equilíbrio quando imerso em uma mistura de dois líquidos imiscíveis de modo que metade está imersa no líquido 1 e outra metade está no líquido 2, como na figura. Quando este mesmo corpo é colocado em um recipiente somente com líquido 2, é correto afirmar que:
Questão 101
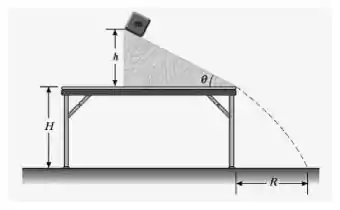
Um bloco de massa é solto do repouso a acima da superfície de uma mesa, no topo de um plano inclinado com , conforme mostrado na figura. O plano inclinado é fixado sobre uma mesa de altura .
- Determine a aceleração do bloco enquanto ele desce escorregando pelo plano inclinado.
- Qual é a velocidade escalar do bloco quando ele deixa o plano inclinado?
- A que distância da mesa o bloco atingirá o solo?
- Quanto tempo leva entre o bloco ser solto e o instante em que atinge o solo?
- A massa do bloco afeta algum dos cálculos precedentes?
Questão 102
Um objeto de massa parte do repouso e, atuado por uma força constante , atinge a velocidade de depois de . Então o valor da força é:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 103
3) Um corpo de massa está sujeito unicamente à ação de três forças constantes, e , no plano , e cujos módulos valem, respectivamente, , e . A situação está ilustrada na figura abaixo, onde o ângulo é tal que e .
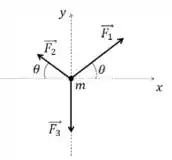
O corpo experimenta uma aceleração que, em termos dos vetores unitários e , está corretamente escrita na alternativa:
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 104
Um corpo de apoiado sobre um plano horizontal sem atrito está submetido a várias forças horizontais, , , e -10 N. Determine a aceleração do corpo.
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 105
Na tirinha, tanto o Cascão, quanto a Mônica, estão fazendo uso da Segunda Lei de Newton ().

Analise as afirmações e selecione as que são verdadeiras.
. O movimento regido pela Segunda Lei de Newton é um movimento uniformemente variável.
. O coeficiente de atrito estático é maior que o coeficiente de atrito cinético.
. O deslocamento sofrido por um corpo que está sobre a ação de uma força resultante é sempre crescente em módulo.
. A velocidade desenvolvida por um corpo sobre a ação de uma força resultante sempre aumenta.
Assinale a alternativa onde só existem afirmações verdadeiras.
(a) e
(b) e
(c) e
(d) e
(e) e
Ver solução completaQuestão 106
Os desenhos animados costumam explorar, muitas vezes de forma inadequada e incorreta,os conceitos relacionados ao estudo da física .
He-Man, um personagem de grande sucesso na década de 80, agradou não só as crianças, mas adultos também. Uma das marcas desse personagem era seu físico único e incomparável e uma força sobre-humana, apontava sua espada para o céu que brilhava entre raios e trovões e dizia sempre: "Pelos poderes de Grayskull, eu tenho a força".
Apesar do grande sucesso desse herói, sua frase sobre a força está incorreta de acordo com o estudo das leis de Newton.
O correto seria He-Man dizer:
a) Minha mão tem muita força!
b) Eu tenho muita força nos músculos!
c) Eu sou capaz de aplicar força de grande intensidade!
d) A força oriunda dos raios que me dão a força!
e) Meu braço tem a força.
Ver solução completaQuestão 107
Uma força igual a (N) atua sobre o bloco , como mostrado na figura abaixo, fazendo com que os blocos , e se desloquem sobre uma superfície horizontal sem atrito. Considere que as massas dos blocos são , e , respectivamente. Encontre o vetor força que o bloco exerce sobre o bloco .
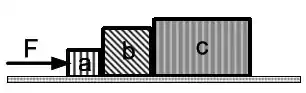
a)
b)
c)
d)
Ver solução completaQuestão 108
Em qual das seguintes situações o trabalho da força resultante é zero?
(A) Uma bola desce um plano inclinado rolando sem deslizar.
(B) Um estudante de física estica uma mola.
(C) Um projétil cai em direção à superfície da Terra.
(D) Uma caixa é puxada ao longo de um plano inclinado áspero com velocidade constante.
(E) Uma criança puxa um brinquedo sobre uma superfície horizontal áspera fazendo com que ele se acelere.
Ver solução completaQuestão 109
Um corpo de massa descreve um movimento acelerado em um plano e tem sua posição em função do tempo dada pelas equações: e . Usar o S.I.
Calcule e escreva em notação vetorial a velocidade do corpo no instante
Calcule e escreva em notação vetorial a força que atua no corpo no instante do item .
Ver solução completaQuestão 110
Questão 3
Considerando um cubo de 8m³ com 7m³ de água apoiado sobre um caminhão em movimento, qual aceleração máxima que o caminhão pode ter para que esse líquido não transborde?
Ver solução completaQuestão 111
Quando um paraquedista pula de um avião, acaba alcançando uma velocidade constante, chamada velocidade terminal. A partir do momento em que essa velocidade terminal é alcançada
- A aceleração do paraquedista é igual a .
- A força de arraste do ar no paraquedista é igual a zero.
- A intensidade da força de arraste do ar no paraquedista é igual a .
- A velocidade do paraquedista é igual a .
- A intensidade da força de arraste do ar no paraquedista é igual a força gravitacional sobre ele.
Questão 112
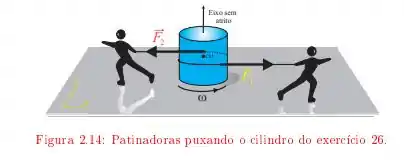
Um disco uniforme de e raio está sobre uma superfície de gelo lisa. Duas patinadoras gêmeas enrolam cordas em torno do disco, num mesmo sentido. Depois cada qual puxa a sua corda e se afasta do disco, exercendo sobre ele forças constantes e durante .
Determine a aceleração, a velocidade e a posição do centro de massa em função do tempo.
Questão 113
39. Uma bola de boliche esférica de massa e raio é lançada com velocidade horizontal e não tem qualquer rotação. O coeficiente de atrito cinético entre a bola e a pista é .
(a) Achar o tempo que a bola escorrega até atingir a condição de rolamento sem deslizamento.
Ver solução completaQuestão 114
Um corpo de massa igual a move-se com velocidade constante de , no intervalo de a . Considere que, a partir de, esse corpo é impulsionado por uma força de módulo constante e de mesmo sentido que a velocidade, durante . O gráfico abaixo ilustra o comportamento da força em função do tempo.
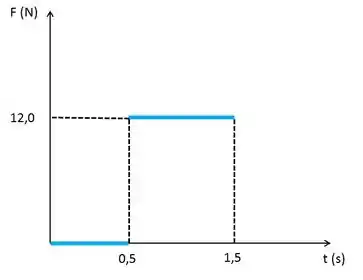
Calcule a velocidade do corpo no instante .
Ver solução completaQuestão 115
[Enunciado comum às Questões 5 e 6]
Sobre um corpo, de massa , atuam três forças, , e . Duas delas, mostradas na figura abaixo à esquerda, tem módulos iguais a , mas atuam em direções diferentes. O corpo está inicialmente em repouso sobre uma mesa horizontal sem atrito. Na figura da direita, é mostrado um gráfico da velocidade escalar do corpo em função do tempo, onde cada quadrado na vertical equivale a . Considere e .
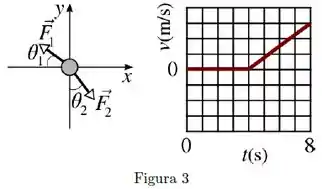
[Questão 5]
Considere as assertivas para o instante :
.
.
.
Marque a alternativa abaixo contendo apenas as assertivas corretas.
(a)
(b)
(c)
(d) e
(e) e
(f) e
(g) Todas
(h) Nenhuma
Ver solução completaQuestão 116
Um paraquedista radical pretende atingir a velocidade do som. Para isso, seu plano é saltar de um balão estacionário na alta atmosfera, equipado com roupas pressurizadas. Como nessa altitude o ar é muito rarefeito, a força de resistência do ar é desprezível. Suponha que a velocidade inicial do paraquedista em relação ao balão seja nula e que a aceleração da gravidade seja igual a . A velocidade do som nessa altitude é . Calcule a distância percorrida nesse intervalo de tempo.
A)
B)
C)
D)
E)
Ver solução completaQuestão 117
Os dois blocos de massas e são empurrados ao longo de uma superfície horizontal sem atrito por uma força , como mostrado na figura.
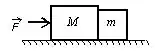
A magnitude da força que um bloco exerce sobre o outro é
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 118
Dois blocos conectados por uma corda passando por uma pequena polia, sem atrito, e em repouso num plano também sem atrito (veja a figura abaixo).
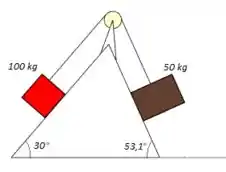
(a) Em que direção o sistema irá se mover quando os blocos forem liberados do repouso?
Ver solução completaQuestão 119
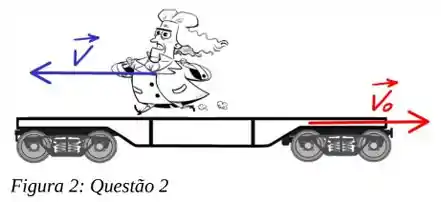
Um vagão de massa M está se movendo com velocidade (em relação ao solo) ao longo de um trilho reto e horizontal. Newton de massa , inicialmente em repouso em relação ao vagão, começa a corre com velocidade (em relação ao vagão). Determine a variação de velocidade observada na velocidade do vagão (em relação ao solo) em termos de
Questão 120
Dois blocos de massas são conectados por uma corda inextensível e de massa desprezível que passa por uma polia (momento de inércia e raio ) presa ao teto. Todo o sistema está inicialmente em repouso com o bloco apoiado no solo enquanto está uma altura acima do solo. Determine a velocidade e a aceleração do bloco quando ele atingir o solo. Considere que a polia gire sem deslizamentos.
Ver solução completaQuestão 121
Um cabo uniforme e rígido de massa e comprimento é cortado em várias partes que são encurvadas e soldadas de modo a formar uma roda circular com quatro raios idênticos que partem do centro. Nada do cabo é desperdiçado e você pode desprezar a massa da solda.
- Se a roda é inicialmente girada com velocidade angular e para uniformemente no instante T, qual é o torque de atrito no seu eixo?
Questão 122
3. Um objeto move-se ao longo de uma linha reta numa superfície horizontal sem atrito. A força resultante sobre o objeto age sempre ao longo da linha do movimento do objeto. O gráfico mostra a velocidade do objeto como função do tempo. Vários intervalos de tempo são indicados pelos algarismos romanos I, II, III, IV e V. Em que intervalo(s) de tempo o módulo da força resultante é variável?
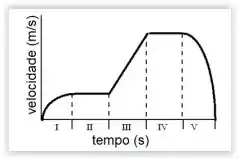
A) I e III
B) II e IV
C) III
D) IV
E) I e V
Ver solução completaQuestão 123
Uma barra uniformemente de comprimento repousa sobre uma superfície horizontal sem atrito. A barra possui um pivô, de modo que ela pode girar sem atrito em torno de um eixo passando por uma das extremidades. A barra está inicialmente em repouso. Uma bala se deslocando com velocidade ortogonal à barra e paralela à superfície atinge o centro da barra e permanece retida em seu interior. A massa da bala é um quarto da massa da barra.
- Qual a velocidade angular final da barra?
Questão 124
Uma barra uniformemente de comprimento repousa sobre uma superfície horizontal sem atrito. A barra possui um pivô, de modo que ela pode girar sem atrito em torno de um eixo passando por uma das extremidades. A barra está inicialmente em repouso. Uma bala se deslocando com velocidade ortogonal à barra e paralela à superfície atinge o centro da barra e permanece retida em seu interior. A massa da bala é um quarto da massa da barra.
- Determine a razão entre a energia cinética do sistema depois da colisão e a energia da bala antes da colisão
Questão 125
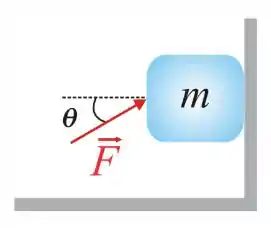
Um bloco de massa é empurrado contra uma parede por uma força que faz um ângulo com a horizontal, como mostra a figura. Se o coeficiente de atrito estático entre a superfície da parede e o bloco vale , calcule qual é o valor mínimo do módulo de que faz que o bloco permaneça estacionário. Dê sua resposta em Newtons.
Adote .
a)
b)
c)
d)
e)
Ver solução completaQuestão 126
Uma massa tem velocidade na origem e move-se ao longo do eixo onde existe um meio onde a força de arrasto depende da velocidade e é dada por
Encontre a função ou e mostre que o objeto percorrerá uma distância máxima de .
Ver solução completaQuestão 128
Para medir o volume de chuva utilizamos um aparelho chamado de pluviômetro. Este é destinado a medir, em milímetros (), a altura da lâmina de água gerada pela chuva que caiu em uma área de . Para chuvas moderadas, o valor esperado é de . Nos dias e de Fevereiro de , São Sebastião e outras cidades do litoral norte passaram por chuvas intensas, as quais foram classificadas como eventos climáticos extremos, pois as estações meteorológicas registraram índices acima de . Estime quantos dias de chuvas moderadas correspondem à quantidade de chuva que ocorreu no litoral norte nos dias e de Fevereiro.
Ver solução completaQuestão 129
Estime:
c) o número de grãos da areia da praia de Copacabana (ou de outra que você conhecer melhor);
Ver solução completaQuestão 131
A sonda cosmológica WMAP (Wilkinson Microwave Anisotropy Probe) determinou em que a densidade média de átomos no Universo é equivalente a próton por .
b) Estime o número total de núcleons (nêutrons e prótons) contido nesse volume;
Ver solução completaQuestão 132
Um dos fenômenos mais comuns presentes na nossa atmosfera é o chamado Equilíbrio Hidrostático, que representa um balanço entre a pressão atmosférica e a força gravitacional. Utilizando análise dimensional, também conseguimos encontrar uma expressão para a pressão (força por unidade de área) de uma coluna de gás em termos da densidade do gás , da altura da coluna e da gravidade . Para isto, responda os itens abaixo.
a) Mais pra frente veremos que o módulo da força em um corpo de massa pode ser expresso por
Onde é a aceleração do mesmo. Utilizando a expressão acima, determine a dimensão de .
Ver solução completaQuestão 133
Considere uma estrela que sofre algum tipo de oscilação. Como a frequência (onde é o período) da oscilação depende das propriedades da estrela? Para entender esse fato através de análise dimensional, responda os itens abaixo.
a) Como sempre o primeiro passo é identificar as variáveis físicas relevantes. Discuta porque aqui as variáveis relevantes são a densidade de massa , o raio da estrela e a constante da lei da gravitação universal de Newton.
Ver solução completaQuestão 134
Estime:
b) o número médio de gotas de chuvas que caem sobre a área de para a precipitação de de chuva;
Ver solução completaQuestão 135
A sonda cosmológica WMAP (Wilkinson Microwave Anisotropy Probe) determinou em que a densidade média de átomos no Universo é equivalente a próton por .
a) Estime a massa total contida dentro do raio do Universo;
Ver solução completaQuestão 136
A sonda cosmológica WMAP (Wilkinson Microwave Anisotropy Probe) determinou em que a densidade média de átomos no Universo é equivalente a próton por .
c) Compare a densidade média de matéria no Universo com a densidade típica do interior do núcleo atômico.
Ver solução completaQuestão 137
Um dos fenômenos mais comuns presentes na nossa atmosfera é o chamado Equilíbrio Hidrostático, que representa um balanço entre a pressão atmosférica e a força gravitacional. Utilizando análise dimensional, também conseguimos encontrar uma expressão para a pressão (força por unidade de área) de uma coluna de gás em termos da densidade do gás , da altura da coluna e da gravidade . Para isto, responda os itens abaixo.
b) Determine a dimensão de .
Ver solução completaQuestão 138
Um dos fenômenos mais comuns presentes na nossa atmosfera é o chamado Equilíbrio Hidrostático, que representa um balanço entre a pressão atmosférica e a força gravitacional. Utilizando análise dimensional, também conseguimos encontrar uma expressão para a pressão (força por unidade de área) de uma coluna de gás em termos da densidade do gás , da altura da coluna e da gravidade . Para isto, responda os itens abaixo.
c) Use análise dimensional para obter em função de , e .
Ver solução completaQuestão 139
Considere uma estrela que sofre algum tipo de oscilação. Como a frequência (onde é o período) da oscilação depende das propriedades da estrela? Para entender esse fato através de análise dimensional, responda os itens abaixo.
b) Determine a dimensão da constante gravitacional .
Ver solução completaQuestão 140
Considere ondas na superfície da água, que são chamada de ondas de gravidade. Como a frequência (onde é o período) dessas ondas depende do chamado número de onda (onde é o comprimento de onda)? Discuta porque as quantidades relevantes aqui são a densidade da água , a aceleração da gravidade e . Use o fato que e análise dimensional para encontrar uma expressão para .
Ver solução completaQuestão 141
Em explosões nucleares há essencialmente uma liberação instantânea de energia em uma pequena região do espaço. Isso produz uma onda de choque esférica, com a pressão dentro da onda de choque milhares de vezes maior que a pressão inicial do ar. Para identificar a dependência do raio da onda de choque com o tempo, responda os itens abaixo:
a) Discuta porque as quantidades relevantes são , e a densidade do ar .
Ver solução completaQuestão 142
Em explosões nucleares há essencialmente uma liberação instantânea de energia em uma pequena região do espaço. Isso produz uma onda de choque esférica, com a pressão dentro da onda de choque milhares de vezes maior que a pressão inicial do ar. Para identificar a dependência do raio da onda de choque com o tempo, responda os itens abaixo:
b) Mais adiante veremos que a energia de uma partícula livre é dada por
Onde representa a massa e a velocidade da partícula. Utilize a expressão acima para mostrar que .
Ver solução completaQuestão 143
Em explosões nucleares há essencialmente uma liberação instantânea de energia em uma pequena região do espaço. Isso produz uma onda de choque esférica, com a pressão dentro da onda de choque milhares de vezes maior que a pressão inicial do ar. Para identificar a dependência do raio da onda de choque com o tempo, responda os itens abaixo:
c) Use análise dimensional para obter .
Ver solução completaQuestão 144
Duas forças horizontais agem sobre um bloco de madeira de que pode deslizar sem atrito na bancada de uma cozinha, situada em um plano . Uma das forças é . Determine a aceleração do bloco em termos dos vetores unitários se a outra força é:
Ver solução completaQuestão 145
Duas forças horizontais agem sobre um bloco de madeira de que pode deslizar sem atrito na bancada de uma cozinha, situada em um plano . Uma das forças é . Determine a aceleração do bloco em termos dos vetores unitários se a outra força é:
Ver solução completaQuestão 146
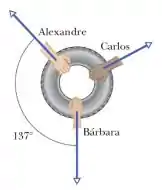
Em um cabo-de-guerra bidimensional, Alexandre, Bárbara e Carlos puxam horizontalmente um pneu de automóvel nas orientações mostradas na Figura. Apesar dos esforços da trinca, o pneu permanece no mesmo lugar. Alexandre puxa com uma força de módulo e Carlos puxa com uma força de módulo . Observe que a orientação de não é dada. Qual é o módulo da força exercida por Bárbara?
Questão 147
Um bloco com um peso de está em repouso em uma superfície horizontal. Uma força para cima de é aplicada ao corpo através de uma mola vertical. Qual é o módulo e o sentido da força exercida pelo bloco sobre a superfície horizontal?
Ver solução completaQuestão 148
Um carro que pesa está se movendo a quando os freios são aplicados, fazendo o carro parar depois de percorrer . Supondo que a força aplicada pelo freio é constante, determine:
O módulo da força aplicada pelo freio;
Ver solução completaQuestão 149
Um carro que pesa está se movendo a quando os freios são aplicados, fazendo o carro parar depois de percorrer . Supondo que a força aplicada pelo freio é constante, determine:
O tempo necessário para o carro parar;
Ver solução completaQuestão 150
Um carro que pesa está se movendo a quando os freios são aplicados, fazendo o carro parar depois de percorrer . Supondo que a força aplicada pelo freio é constante, determine:
Se a velocidade inicial é multiplicada por dois e o carro experimenta a mesma força durante a frenagem, por que fatores são multiplicados:
O tempo necessário para o carro parar?
Ver solução completaQuestão 151
Considere uma estrela que sofre algum tipo de oscilação. Como a frequência (onde é o período) da oscilação depende das propriedades da estrela? Para entender esse fato através de análise dimensional, responda os itens abaixo.
c) Utilizando análise dimensional, determine a dependência de com as propriedades da estrela.
Ver solução completaQuestão 152
Dados os vetores: e encontre:
a)
b)
c)
d) o valor de e de
e) o cosseno do ângulo entre e
f)
Ver solução completaQuestão 153
Considere dois pontos localizados em posições e , de tal forma que esses pontos estão separados por uma distância . Encontre uma expressão para o vetor que vai da origem até um ponto na reta que liga a , e que está a uma distância do ponto , onde é algum número (por simplicidade, imagine ).
Ver solução completaQuestão 154
Você está dirigindo um Maseratti GranTurismo S ao longo de uma pista retilínea de teste com velocidade escalar constante igual a . Você ultrapassa em um fusca Volksvagen que se move com velocidade escalar constante igual a . Para qual dos dois carros a força resultante é maior?
Ver solução completaQuestão 155
Duas forças horizontais agem sobre um bloco de madeira de que pode deslizar sem atrito na bancada de uma cozinha, situada em um plano . Uma das forças é . Determine a aceleração do bloco em termos dos vetores unitários se a outra força é:
Ver solução completaQuestão 156
Uma partícula de se move no plano de acordo com as equações e , e em metros e em segundos. No instante . Qual é o vetor força resultante a que está submetida a partícula?
Ver solução completaQuestão 157
Um carro que pesa está se movendo a quando os freios são aplicados, fazendo o carro parar depois de percorrer . Supondo que a força aplicada pelo freio é constante, determine:
Se a velocidade inicial é multiplicada por dois e o carro experimenta a mesma força durante a frenagem, por que fatores são multiplicados:
a distância até o carro parar;
Ver solução completaQuestão 158
Dois blocos estão em contato em uma mesa sem atrito. Uma força horizontal é aplicada ao bloco maior, como mostra a Figura. Se e .
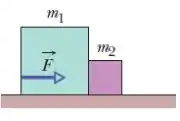
Mostre que se uma força de mesmo módulo de for aplicada ao menor dos blocos no sentido oposto, o módulo da força entre os blocos será , que não é o mesmo valor calculado no item anterior.
Ver solução completa