Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 2.1 - Ex. 108
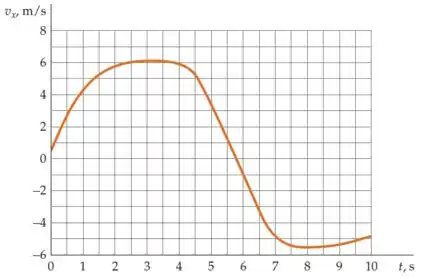
A figura abaixo é um gráfico da velocidade em função do tempo para uma partícula se movendo ao longo de uma linha reta. A posição da partícula em um tempo é . (a) Encontre para valores variados de contando os quadrados do gráfico, e então esboce em função de . (b) Esboce um gráfico da aceleração como função do tempo . (c) Determine o deslocamento da partícula entre e .
Passo 1
a) Queremos saber os valores de para diferentes . A ideia é que ele deu a posição inicial e a gente vai conseguir achar o deslocamento do objeto em alguns instantes pelo gráfico.
E com isso, o nosso valor de para um ponto vai ser
Mas como podemos achar o deslocamento a partir de um gráfico da velocidade em função do tempo? É só calcular a área sob a curva, podemos fazer isso “contando” os quadrados da malha quadriculada no gráfico do enunciado.
Então para alguns valores de , a gente vai calcular quantos quadrados há sob o gráfico da curva de até o em questão.
Mas quanto “vale” cada quadrado na malha? Vamos calcular a área de cada um deles. Para o eixo horizontal, dois quadrados têm a distância de , então um quadrado tem a distância de . Já no eixo vertical, um quadrado vai ter a distância de . A área fica:
Ou seja, para cada quadrado sob a curva, podemo contar de deslocamento. Para fazer a contagem, é útil desenhar o eixo horizontal na posição “correta”, em :
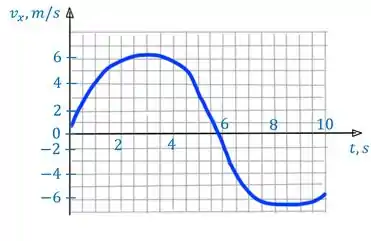
E a gente vai considerar os quadrados abaixo do eixo (velocidade negativa) como “negativos”, então eles vão entrar com sinal de menos na contagem de quadradinhos.
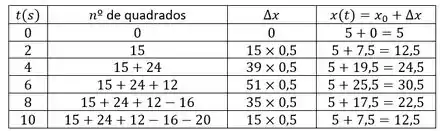
Como nosso objetivo é plotar o deslocamento em função do tempo, vamos fazer essa contagem para vários intervalos de tempo, terminando entre e .
Passo 2
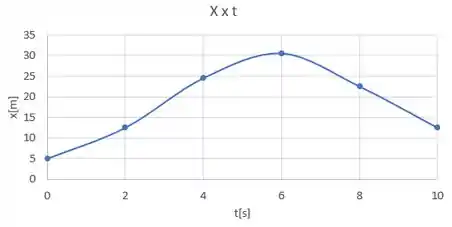
Agora vamos usar os dados que coletamos para esboçar um gráfico de . A ideia é basicamente plotar esses pontos em um plano e depois traçar uma curva que passe por eles:
Passo 3
E agora vamos fazer um esboço do gráfico da aceleração. Em um gráfico da velocidade em função do tempo, a aceleração é a inclinação da reta tangente em cada ponto.
Para cada ponto em que quisermos estimar a aceleração instantânea, vamos ter que considerar um pequeno intervalo do gráfico, em torno desse ponto.
Vamos começar com um pequeno trecho do gráfico, em que vamos estimar , e .
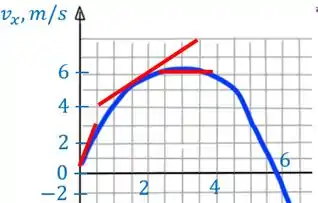
Os segmentos vermelhos tangentes foram prolongados ou encurtados até que cruzassem algum ponto que facilitasse o cálculo da aceleração:
Passo 4
Agora vamos fazer a mesma coisa para outro trecho do gráfico, para estimar os , e :
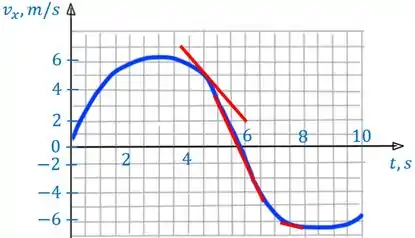
Essa última não foi sequer calculada, pois é visível que a inclinação da reta é próxima de zero, pois a reta é quase horizontal.
E então podemos usar esses pontos (e um pouco de bom senso, já que temos o gráfico completo da velocidade), para fazer o gráfico de .
É só plotar os pontos no plano e traçar uma curva aproximada.
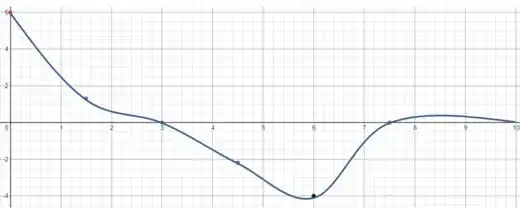
Passo 5
(c) Fica faltando apenas determinar o deslocamento da partícula no intervalo , para isso podemos aproveitar o gráfico de que fizemos lá em cima:
Então:
Resposta
(a)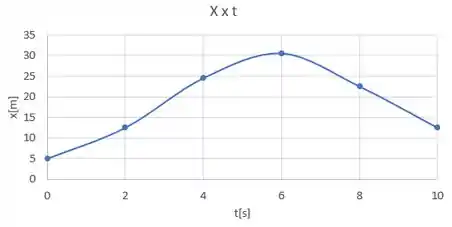 
(b)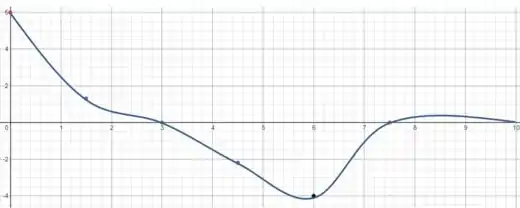 
(c) .