Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Tipler - Vol 2- Ed: 6º - Capítulo 22.1 - Ex. 69

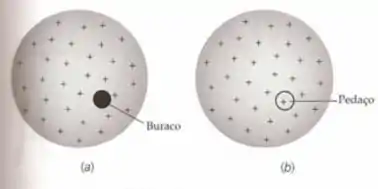
Uma fina casca esférica não condutora, uniformemente carregada, com raio R , tem uma carga total positiva igual a Q ; Um pequeno pedaço é removido da superfície. (a) Quais são o módulo, a direção e o sentido do campo elétrico no centro do buraco? (b) O pedaço é colocado de volta no buraco. Usando o resultado da parte (a), determine a força elétrica exercida no pedaço. (c) Usando a magnitude da força, calcule a “pressão eletrostática” (força/unidade de área) que tende a expandir a esfera.

Passo 1

Fala galera, blz? Esse exercício possui uma ideia um pouquinho complicada. Mas vamos lá, com calma que tudo vai dar certo.

Passo 2

Para começar, vamos dividir o campo elétrico, na parte (a) como sendo a soma de dois campos elétricos:

  1. O campo elétrico da pequena parte escura; E 1 .
  2. O campo elétrico do restante da esfera: E 2 .

O campo elétrico nas proximidades do condutor é:

E = σ ε 0

Dessa forma, devemos ter

E 1 + E 2 = σ ε 0

No interior, o campo elétrico é nulo. Assim, devemos ter

E 1 - E 2 = 0 E 1 = E 2

Dessa forma, vemos que:

E 1 = E 2 = σ 2 ε 0

Passo 3

  1. Quando a gente retira a pequena parte escura, o campo elétrico some. Dessa forma, o campo elétrico no centro será simplesmente

    2. E = σ 2 ε 0 = Q / 4 π R 2 2 ε 0 = Q 8 π ε 0 R 2

    A direção e o sentido do campo elétrico, é do centro até o buraco retirado.

    Passo 4

  2. A força pode ser calculada por:

    3. F = Q b u r a c o E 2 F = σ A b u r a c o E 2 = σ A b u r a c o ⋅ σ 2 ε 0 F = σ 2 2 ε 0   A b u r a c o

    Suponha que A b u r a c o = π a 2 onde a é o raio do buraco. Assim,

    F = Q 2 a 2 32 π ε 0 R 4

  3. A pressão é dada por

P = F A b u r a c o = Q 2 32 π 2 ε 0 R 4

Resposta

  1. σ 2 ε 0
  2. Q 2 a 2 32 π ε 0 R 4
  3. Q 2 32 π 2 ε 0 R 4
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas placas metálicas quadradas idênticas têm, cada uma, área de 500c m 2 . Elas são separadas por 1,50c m e estão, ambas, inicialmente descarregadas. A seguir, uma carga de + 1,50n C é transferida da
Uma lâmina plana infinita não condutora tem uma densidade superficial de carga + 3,00μ C / m 2 e está no plano y = - 0,600m . Uma segunda lâmina plana infinita tem densidade superficial de carga de -
Dois planos infinitos não condutores uniformemente carregados são paralelos entre si e ao plano y z . Um está em x = - 2,00m e tem uma densidade superficial de carga de - 3,50μ C / m 2 . O outro está
Estime a densidade superficial máxima de carga que pode existir na extremidade de um para raios para que não ocorra a ruptura dielétrica do ar.
29 . Um condutor cilíndrico infinito possui raio R e densidade superficial de carga σ . ( a ) Em função de σ e R , qual é a carga por unidade de comprimento λ para o cilindro? ( b ) Em função de σ , q