Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 4.1 - Ex. 55
(a) Trabalhemos uma solução numérica ao Problema 54. Escreva um programa para planilha eletrônica que faça um gráfico da forma do arco de balões. Use os seguintes parâmetros: (balões), cada um contribuindo com uma força de sustentação e todos eles atados a uma corda de comprimento , com uma componente horizontal de tensão Qual a distância entre os dois pontos de amarração da corda? Qual a altura do ponto mais alto do arco? (b) Note que não especificamos os espaçamentos entre os pontos de amarração – ele é determinado pelos outros parâmetros. Varie , mantendo os outros parâmetros inalterados, até criar um arco com o espaçamento de 8,0 m entre os pontos de amarração. Neste caso, quanto vale ? Enquando você aumenta , o arco deve se tornar mais achatado ou menos achatado? Seu modelo de planilha eletrônica mostra este resultado?
Passo 1
a) Oi pessoal, tudo bem? Vamos analisar essa questão. Ele quer que a gente faça um gráfico da forma do arco de balões do problema anterior.
Esse arco é uma curva, certo? Aí para fazer uma curva, o que a gente precisa são pontos que pertencem a ela. E como a gente acha esses pontos?
Cara, essa curva é formada pelos pontos inicial e final da corda e pelos balões. Então que a gente precisa para começar é saber as posições dos balões e a posição inicial da corda.
A posição inicial a gente pode escolher como sendo a origem do nosso referencial . E as coordendas dos balões? Bem, para saber as coordenadas dos balões, a gente vai olhar o enunciado do problema 54. Lá ele diz que para esse arco, valem as equações:
Percebe que ele dá que vão ser as coordenadas dos pontos que a gente precisa usar.
A ideia é a gente usar essa equações e os parâmetros que ele deu para fazer o nossos gráfico.
Como ele pede para usar uma planilha eletrônica, vamos usar o excel aqui. Mas você pode usar outros softwares também. Vamos lá!
Passo 2
é o ângulo do ponto inicial do arco, onde ele está amarrado. Podemos encontra-lo isolando dess equação:
Os valores de e são dados pelo enunciado:
Então a gente substitui elas ali na equação de e acha seu valor. Vamos mostrar o resultado na planilha, junto com os outros.
Já seria o ângulo de um ponto da curva. A gente vai tirar ele dessa equação:
Novamente, é substituir os parâmetros que e ele dá e partir para o abraço. Lembrando que temos 10 balões. Então temos um total de 12 pontos, começando de que é o ponto inicial onde a corda está presa e terminando em que é o ponto final da corda, onde ela está amarrada também.
Usamos essas fórmulinhas, achamos os ângulos para cada ponto:
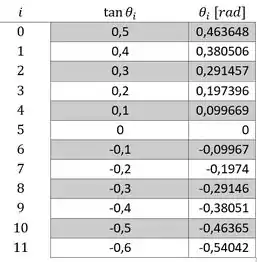
Passo 3
Para achar a posição para cada ponto depois de (que a gente já definiu como , vamos usar:
Sendo que . Mas o que significa esse somatório? Cara, para entender isso vamos imaginar que queremos , ok?
Então vamos substituir esse cara no somatório e abrir o somatório:
Vê que o único termo que esse somatório vai ter é . Então percebe que a posição depende do ângulo da posição anterior a ele.
Agora vamos ver :
Percebe que agora o somatório teve 2 termos. Vamos fazer a distributiva:
Repara que esse primeiro termo é a posição de que a gente acabou de calcular. Então podemos dizer que:
Olhando para essa expressão, a gente vê que depende da posição de anterior a ele e depende do cosseno de , o ângulo do ponto anterior. Se a gente fizer isso para e os outros ponto, vamos ver que esse padrão de usar informações do ponto anterior se repete.
Aí de forma geral, a gente pode escrever que a posição é dada por:
O termo indica esse uso de informações do ponto anterior a .
Passo 4
Aí para a posição a gente pode usar o mesmo raciocínio do passo anterior para perceber que
Podemos ser reescrito como:
Ou seja, vai usar informações do ponto imediatamente anterior a ele, assim como .
Com essas duas expressões de e , usando os valores de que ele deu e sabendo que , a gente pode calcular os pontos que pertencem ao nosso arco:
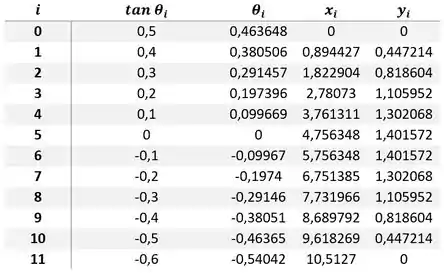
Percebe que a posição da segunda amarração da corda ao solo é achada também por essas expressões que usamos para onde .
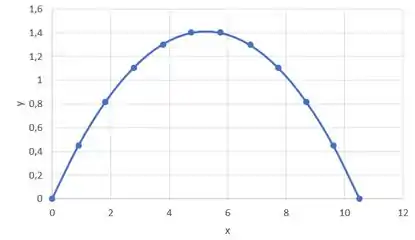
E com esses pontos, a gente pode fazer o gráfico que representa o arco:
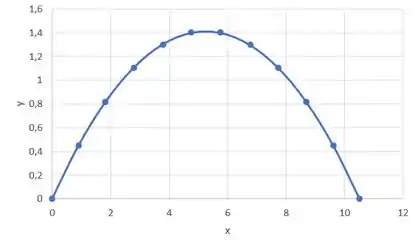
Passo 5
Ele quer saber a distância entre os dois pontos de amarração da corda que na real é a distância entre o ponto final e inicial da nossa curva, que estão na mesma altura, então a gente pode escrever:
Obs: aqui ficou um pouco diferente do gabarito, mas estamos certinhos, tá?
E ele quer a altura máxima do arco. É só a gente vê o maior valor de que ele atinge. Pelo gráfico temos
Passo 6
b) Queremos achar para que . Aí a gente vai variar o nosso valor de ali na nossa planilha:
Por exemplo, se a gente fizer na planilha, achamos . Muito baixo. Agora se a gente fizer já achamos . Muito alto.
Pensando em um número entre eles, podemos fazer . Aí conseguimos . Bem pertinho do que a gente quer, né? Vamos testar números bem próximos desses até achar certinho.
Fazendo a gente chega em . Então a gente pode considerar que uma componente horizontal de tensão, , nos dá um espaçamento de aproximadamente 8 m.
Passo 7
E por fim ele quer saber se um aumento em deixa o arco mais ou menos achatado.
Cara, pela figura (b) do problema 54, a gente vê que se tiver uma componente horizontal cada vez maior, menor vai ser o ângulo . Isso quer dizer que os segmentos que forma o arco vão tender a estar mais perto de serem horizontais. E assim, achatando o arco.
E ele quer saber se é isso que acontece com o arco da nossa planilha. Viu que quando a gente fex , tivemos uma largura do arco de , mas quando a gente aumentou para , tivemos . E ainda, quando a gente tinha , achamos .
Ou seja, quando maior , mais largo é o arco. Se o tamanho da corda é sempre o mesmo, isso significa que o arco está ficando mais achatado conforme é maior.
Então nosso modelo preveu sim que aumentar deixaria o arco mais achatado.
Obs: ficamos diferentes do gabarito nos valores mas estamos certinhos, tudo bem?
Resposta
a)
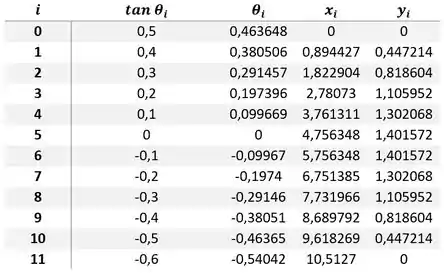
b)
Quando maior mais achado o arco fica.