Exercícios de Força Magnética - Lista de Exercícios Resolvida
Questão 1
Uma câmara de bolhas, representada na figura abaixo, possui um campo magnético constante (estacionário e uniforme) , perpendicular à folha de papel. Uma partícula neutra, em repouso no centro da câmara, transforma-se (decai) em outras partículas, cujas trajetórias são mostradas na figura. Quanto à carga dessas partículas resultantes do decaimento, podemos afirmar que:
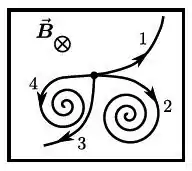
- Todas as partículas e tem carga zero.
- As partículas e tem cargas positivas, ao passo que as partículas e tem cargas negativas.
- As partículas e tem cargas negativas, ao passo que as partículas e tem cargas positivas.
- As partículas e tem cargas positivas, ao passo que as partículas e tem cargas negativas.
- As partículas e tem cargas positivas, ao passo que as partículas e tem cargas negativas.
Questão 2
Uma partícula carregada com carga e massa é acelerada paralelamente ao eixo , no sentido de crescente, a partir do repouso, por uma diferença de potencial .
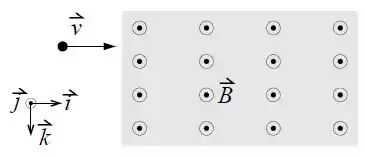
Determine o vetor velocidade final da partícula após a aceleração do potencial .
A partícula carregada adentra a seguir numa região de campo magnético uniforme . Determine o vetor força magnética que atua sobre a partícula em função de , , e .
Faça um esquema do movimento dessa partícula na região de campo . Calcule o raio da trajetória na região com campo magnético e o tempo gasto nesta região.
Ver solução completaQuestão 3
Uma partícula alfa se move com uma velocidade de módulo em uma região onde existe um campo magnético de módulo Uma partícula alfa possui uma carga de e uma massa de . O ângulo entre é .
Dados:
Determine:
O módulo da força que o campo magnético exerce sobre a partícula.
A aceleração da partícula causada por
A velocidade da partícula aumenta, diminui ou permanece constante?
Ver solução completaQuestão 4
Na figura abaixo, uma partícula descreve uma trajetória circular em uma região onde existe um campo magnético de módulo , cujo sentido é mostrado na figura. A partícula pode ser um próton ou elétron (a identidade da partícula faz parte do problema) e está sujeita a uma força magnética de módulo igual a .
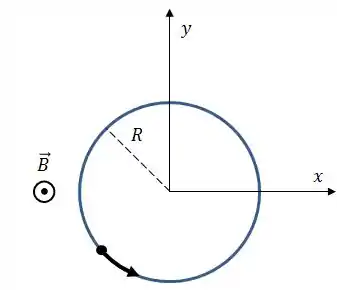
Determine:
A velocidade escalar da partícula;
Explicar qual partícula está girando em ;
O raio da trajetória;
O período do movimento;
Ver solução completaQuestão 5
Uma partícula com massa de e carga de se move em uma região onde existe um campo magnético uniforme e a aceleração da gravidade é . A velocidade da partícula é constante e igual a , perpendicular ao campo magnético. Qual é o campo magnético?
Ver solução completaQuestão 6
Um próton (carga , massa ), um dêuteron (carga , massa ), e uma partícula alfa (carga , massa ) entram numa região com campo magnético uniforme , todas com a mesma velocidade .
Sabendo-se que e que o próton se move numa circunferência de raio , podemos dizer que os raios das órbitas circulares do dêuteron e da partícula alfa são, respectivamente:
e .
e .
e .
e .
e .
Ver solução completaQuestão 7
Um elétron com uma velocidade
está se movendo em uma região onde existe um campo magnético uniforme .
- Determine a força que age sobre o elétron.
- Repita o cálculo para um próton com a mesma velocidade.
Questão 8
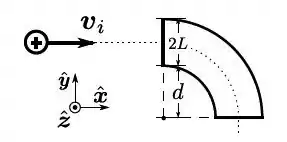
Um acelerador de partículas é projetado para desviar um próton, de massa e carga , que incida horizontalmente, com velocidade inicial , para uma velocidade final . Assinale o campo magnético constante que permite que isso aconteça.
Questão 9
Em um espectrômetro de massa, um feixe de íons emitido por uma fonte atravessa uma região de campo magnético uniforme e estacionário, como mostrado na figura abaixo.
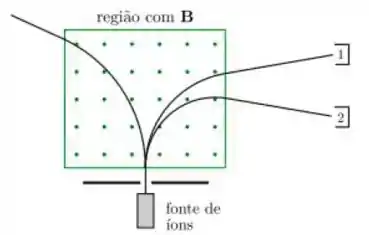
Esse sistema é utilizado para determinar a quantidade de água pesada (, onde representa um átomo de deutério) que há na água do mar. Como resultado da ionização, separa-se apenas os íons , e , que são então acelerados de forma a entrar na região de campo magnético com a mesma velocidade inicial. Sabendo que as massas dos átomos de , e valem 1, 2 e 16 u.m.a, respectivamente, e que a massa do elétron pode ser desprezada em confronto com as massas do próton e do nêutron, podemos afirmar que os íons coletados nos detectores 1 e 2, respectivamente,
- e
- e
- e
- e
- e
Questão 10
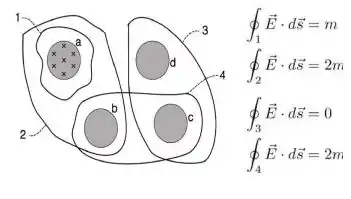
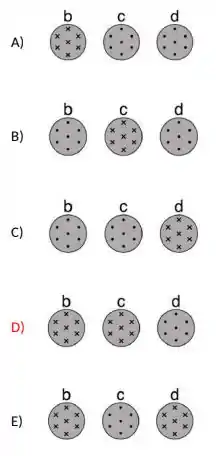
A figura mostra quatro regiões, indicadas pelas letras 'a', 'b', 'c' e 'd', nas quais um campo magnético perpendicular à folha de papel varia no tempo. Nas quatro regiões, o campo magnético aumenta, em módulo, a taxas iguais. A integral de linha do campo elétrico ao longo das quatro curvas fechadas, numeradas de 1 a 4, está expressa em termos de uma constante . Qual alternativa indica corretamente o sentido do campo magnético nas regiões 'b', 'c' e 'd'?
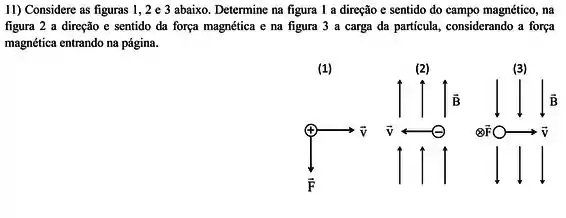
Questão 11
A corrente flui da esquerda para a direita no condutor mostrado. O campo magnético está dirigido para “dentro” da página e o ponto S está a um potencial maior que o ponto T. Os portadores de carga:
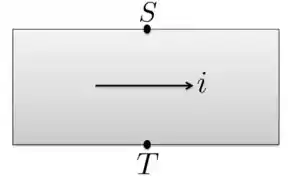
- São negativos;
- São positivos;
- São neutros;
- São ausentes;
- Movem-se com velocidade próxima à da velocidade da luz.
Questão 12
Considere as seguintes afirmações, com respeito a um referencial inercial dado:
(I) Uma partícula carregada em movimento em um campo magnético nunca segue uma trajetória retilínea.
(II) Quando sobre a partícula há outras forças além da magnética, a força magnética pode realizar trabalho ao longo da trajetória real da partícula.
(III) A força magnética sobre uma partícula carregada nunca pode alterar o módulo da sua velocidade.
Qual(is) delas é(são) verdadeira(s)?
(a) Somente a II.
(b) Somente a III.
(c) Somente a I e a III.
(d) Somente a II e a III.
(e) Nenhuma.
Ver solução completaQuestão 13
Um próton (carga , massa ), um dêuteron (carga , massa ), e uma partícula alfa (carga , massa ) entram numa região com campo magnético uniforme , todas com a mesma velocidade .
Sabendo-se que e que o próton se move numa circunferência de raio , podemos dizer que os raios das órbitas circulares do dêuteron e da partícula alfa são, respectivamente:
e .
e .
e .
e .
e .
Ver solução completaQuestão 14
Na figura abaixo, uma partícula (que pode ser um próton ou um elétron) descreve uma trajetória circular em uma região onde existe um capo magnético uniforme de módulo igual a (saindo do plano do papel). A partícula está sujeita a uma força magnética de módulo igual a .

Identifique o sinal da carga da partícula (justifique);
Determine:
A velocidade escalar da partícula;
O raio da trajetória da partícula;
O período do movimento;
Dados:
massa do próton:
massa do elétron:
Ver solução completaQuestão 15
Na figura abaixo, uma partícula descreve uma trajetória circular em uma região onde existe um campo magnético de módulo , cujo sentido é mostrado na figura. A partícula pode ser um próton ou elétron (a identidade da partícula faz parte do problema) e está sujeita a uma força magnética de módulo igual a .
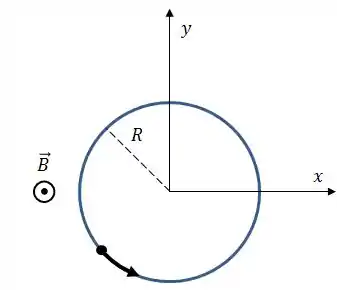
Determine:
A velocidade escalar da partícula;
Explicar qual partícula está girando em ;
O raio da trajetória;
O período do movimento;
Ver solução completaQuestão 16
No esquema da figura 1 estão representadas uma esfera compacta de material isolante de raio e uma casca condutora, concêntrica com ela, de raio interno e raio externo . A esfera isolante está carregada uniformemente com densidade volumétrica de carga . A casca condutora tem carga total nula.
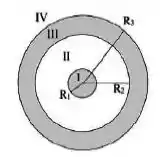
- Qual a carga e como está distribuída nas superfícies interna e externa do condutor?
Questão 17
Duas cargas positivas iguais a estão situadas em cantos opostos de um quadrado de lado . Duas outras cargas negativas, estão situadas nos outros dois cantos restantes.
- Qual o valor de se a força que age sobre a carga for zero?
Questão 18
Duas cargas positivas iguais a estão situadas em cantos opostos de um quadrado de lado . Duas outras cargas negativas, estão situadas nos outros dois cantos restantes.
- Qual o módulo, a direção e o sentido da força em cada carga com o valor obtido de no item a)?
Questão 19
No esquema da figura 1 estão representadas uma esfera compacta de material isolante de raio e uma casca condutora, concêntrica com ela, de raio interno e raio externo . A esfera isolante está carregada uniformemente com densidade volumétrica de carga . A casca condutora tem carga total nula.
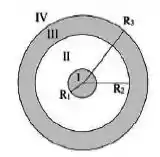
- Suponha agora que a casca condutora é retirada e em seu lugar colocamos duas cascas esféricas isolantes, de espessuras desprezíveis, de raios e com a mesma distribuição de carga que havia no condutor. Qual o vetor do campo elétrico nas regiões ?
Questão 20
Uma barra metálica de comprimento , massa e resistência total está sobre trilhos metálicos sem atrito, inclinados em um ângulo em relação à horizontal. Os trilhos possuem resistência desprezível. Um campo magnético uniforme de módulo está orientado para baixo, como indicado na figura abaixo. A barra é liberada a partir do repouso e desliza para baixo sobre os trilhos.
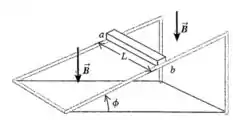
b) Qual é a velocidade terminal da barra?
c) Qual será a corrente induzida na barra quando a velocidade terminal for atingida?
d) Depois que a velocidade terminal da barra for atingida, qual será a taxa de conversão de energia elétrica em energia térmica na barra?
e) Depois que a velocidade terminal da barra for atingida, qual é a taxa do trabalho realizado pela força da gravidade? Compare a sua resposta com o que foi encontrado no item (d).
Ver solução completaQuestão 21
- Um próton move-se em um campo magnético , com uma velocidade de , na direção e no sentido mostrado na figura.
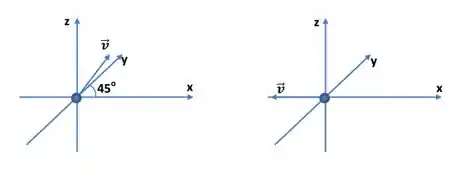
- a) Qual é a força magnética sobre o próton, em cada figura? Expresse sua resposta em função de componentes.
Ver solução completa
Questão 23
Na figura abaixo um fio retilíneo muito longo conduz uma corrente e uma espira
retangular de lados conduz uma corrente . Suponha que e e .
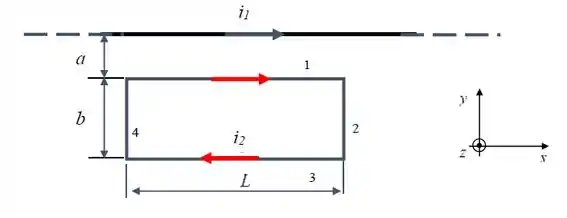
Calcule a força magnética F total (módulo, direção e sentido) a que está submetida espira.
Ver solução completaQuestão 24
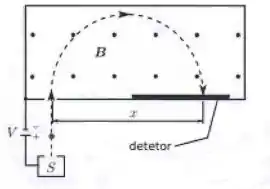
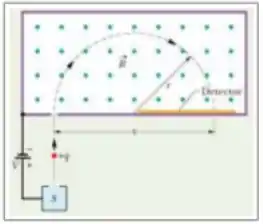
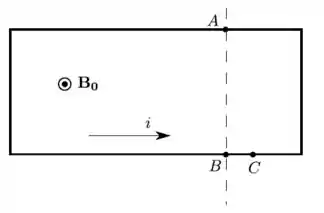
A figura abaixo representa um espectrômetro de massa, aparelho usado para medir a massa de íons. Um íon de massa , a ser determinada, e carga é produzido na fonte , em repouso, e acelerado pelo campo eletrostático associado a uma diferença de potencial . O íon entra em uma câmara de separação na qual existe um campo magnético constante (uniforme e estacionário), perpendicular à sua trajetória. Suponha que o íon atinja o detector em um ponto situado a uma distância do ponto de entrada da câmara. Qual é a massa do íon?
(a)
(b)
(c)
(d)
(e)
Questão 25
PARTE
Uma partícula carregada de massa e carga total penetra numa região do campo com campo magnético constante através do ponto como indicado na figura abaixo. Ao entrar nessa região, a partícula apresenta uma velocidade de entrada , onde . Dentro dessa região, a partícula interage com o campo magnético e torna a sair no ponto , localizado a uma distância e com velocidade de saída igual a . Todos os vetores estão de acordo com o sistema de coordenadas apresentado na figura.
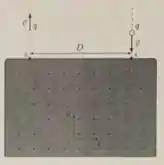
- Qual é o valor (módulo) do campo magnético na região?
- Qual foi o trabalho realizado pela força magnética?
- Encontre o campo magnético (módulo, direção e sentido) causado pelo conjunto de fios retilíneos de comprimento no ponto .
- Encontre o campo magnético (módulo, direção e sentido) causado pelo semicírculo no ponto .
PARTE
Como está representado na figura abaixo, uma corrente de intensidade percorre um fio dividido em três partes. Entre os pontos e , a corrente atravessa um fio retilíneo de comprimento entre os pontos e atravessa um semicírculo de raio e, por fim, entre os pontos e atravessa um outro fio retilíneo de mesmo comprimento .
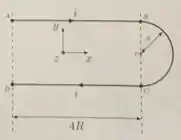
Utilizando explicitamente a lei de Biot-Savart e utilizando o sistema de referência fornecido:
Questão 26
. Uma partícula de carga , inicialmente com velocidade , penetra numa região com campo elétrico uniforme e campo magnético uniforme , ambos estacionários, com e . Ao sair desta região, a partícula possui velocidade e está a uma distância de um eixo horizontal, como mostrado na figura abaixo:
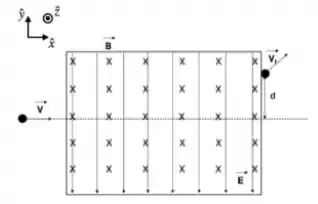
Considere as seguintes afirmativas:
A força que o campo elétrico exerce sobre a partícula realiza trabalho negativo.
Quais destas afirmativas são VERDADEIRAS?
Escolha uma opção:
e
e
e
Nenhuma
e
.
.
Ver solução completaQuestão 28

(A) iguais, .
(B) iguais,
(C)
(D) iguais
(E) Todas possuem massas iguais
Ver solução completaQuestão 29
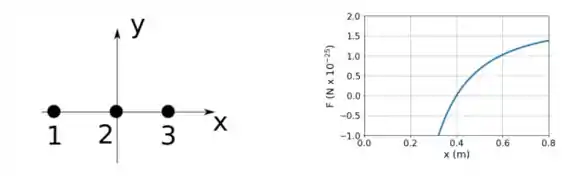
A figura abaixo mostra duas partículas carregadas, 1 e 2, que estão fixas sobre o eixo . O módulo da carga da partícula 1 é , onde é a carga elementar. A partícula 3, de carga , pode ser movida na parte positiva do eixo . O gráfico abaixo mostra a componente da força eletrostática resultante sobre a partícula 2, em função da posição da partícula 3 no eixo. A escala do eixo é dada por . A curva possui uma assíntota para . Use
a) (1,0 ponto) Determine o sinal da carga . JUSTIFIQUE SUA RESPOSTA!
b) (1,5 pontos) Calcule o valor da carga em função da carga elementar . Sugestão: Calcule tudo em função da carga elementar .
Questão 30
Uma partícula de massa e carga , é lançada no ponto com velocidade escalar , descrevendo a trajetória conforme a figura abaixo.
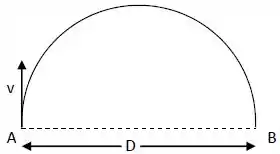
Assinale a opção correta que representa o campo magnético que atua sobre a partícula e o tempo necessário para ela se deslocar de até .
Ver solução completa
Questão 32
Uma barra metálica descarregada se move para a direita com velocidade constante . A barra se encontra imersa em um campo magnético constante, apontando para dentro da página tal como indicado na figura abaixo.
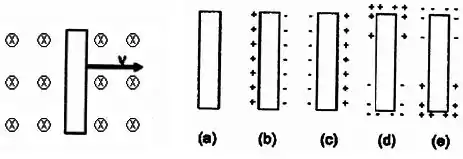
Escolha o diagrama que melhor descreve a distribuição de cargas na superfície da barra. Suponha que os portadores de carga na barra são elétrons.
Ver solução completaQuestão 33
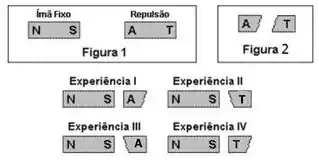
Um imã, em forma de barra, de polaridade (norte) e (sul), é fixado numa mesa horizontal.
Outro imã semelhante, de polaridades desconhecidas, indicadas por e , quando colocado na posição mostrada na figura 1, é repelido para a direita. Quebra-se esse imã ao meio (como mostra a figura 2) e, utilizando as duas metades, fazem-se quatro experiências, representadas nas figuras , , e , em que as metades são colocadas, uma de cada vez, nas proximidades do imã fixo.
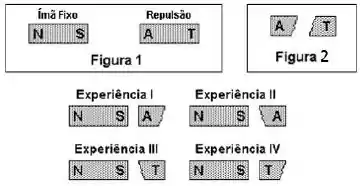
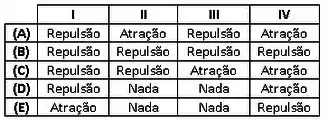
Indicando por "nada" a ausência de atração ou repulsão da parte testada, os resultados das quatro experiências são respectivamente:
- repulsão; - atração; - repulsão; - atração.
- repulsão; - repulsão; - repulsão; - repulsão.
- repulsão; - repulsão; - atração; - atração.
- repulsão; - nada; - nada; - atração.
- atração; - nada; - nada; – repulsão.
Ver solução completaQuestão 34
Um elétron se move com uma velocidade constante de ao longo do eixo positivo, na presença de um campo magnético uniforme e de um campo elétrico uniforme.
O campo magnético aponta para dentro da página e tem módulo de .
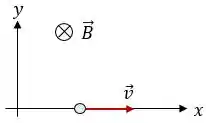
Quais são o módulo e a orientação do vetor campo elétrico.
, no sentido de negativo;
, no sentido de positivo;
, no sentido de negativo;
1, no sentido de negativo;
, no sentido de positivo;
Ver solução completaQuestão 35
Um acelerador de partículas é projetado para desviar um elétron, de massa e carga , que incida horizontalmente, com velocidade inicial , para uma velocidade final . Assinale o campo magnético constante que permite que isso aconteça.
Questão 36
Uma barra metálica neutra está se movendo com velocidade constante para a direita, em uma região onde há um campo magnético constante e uniforme apontando perpendicularmente para fora da página. Qual dos seguintes diagramas descreve melhor a distribuição de cargas na superfície da barra metálica?
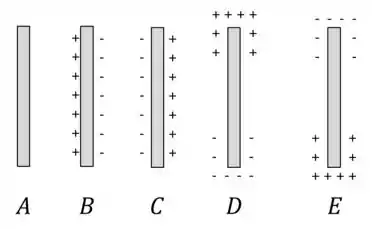
a)
b)
c)
d)
e)
Ver solução completaQuestão 38
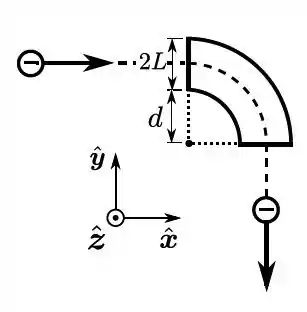
Uma partícula pontual de massa m e carga (positiva) se move com velocidade de módulo constante de tal forma que, como mostra a Figura 1, sua trajetória é descrita pela linha tracejada. Essa partícula penetra em uma região de campo magnético constante (região cinza- escuro) e realiza um movimento circular de raio (ao longo de um arco de graus). Em seguida, penetra em outra região de campo magnético constante (região cinza-claro) e realiza um movimento circular de raio r (ao longo de um arco de graus). Observe que :
- Calcule a razão (módulos dos campos magnéticos).
-
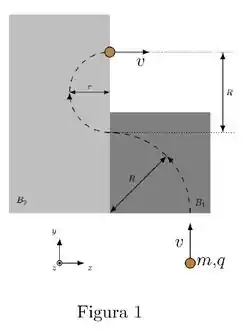
m = 1,0 × 10 - 3 k g , , e , encontre os vetores campos magnéticos em ambas as regiões.
Questão 39
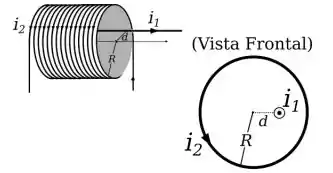
Um solenoide ideal de raio e densidade espiras por metro transporta uma corrente de intensidade . Um fio longo que transporta uma corrente de é posicionado paralelamente ao eixo do solenoide e a uma distância do seu eixo. Qual é a magnitude do campo magnético resultante em um ponto pertencente ao eixo do solenoide?
Questão 40
Em uma região do espaço existe um campo magnético de magnitude (onde ). Um aro condutor, de resistência constante , é descrito pela equação no plano
onde é uma constante com dimensão de tempo. Esse aro se expande com o tempo.
a) Calcule o fluxo magnético no aro como função do tempo.
b) Calcule a f.e.m. no aro e a corrente sobre o mesmo. Justifique se a corrente flui no sentido horário ou anti-horário quando a orientação positiva do aro é dada pelo vetor unitário (ou seja, o sentido positivo é o anti-horário).
c) Calcule a energia total dissipada no aro entre os instantes e .
Ver solução completaQuestão 41
Na figura abaixo, duas partículas pontuais, de massas distintas e , e cargas elétricas idênticas e positivas de valor , deslocam-se ao longo do eixo com velocidades constantes dadas por .
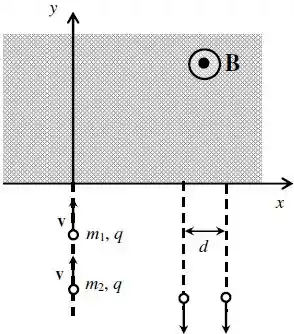
Tais partículas penetram a região , onde existe um campo magnético uniforme , perpendicular ao plano e saindo do plano da página.
Considere que o campo magnético é nulo fora da região . Sabe-se que, ao saírem da região , as partículas movem-se em trajetórias retilíneas e paralelas entre si.
Calcule o comprimento das trajetórias descritas pelas partículas, na região .
Calcule o trabalho realizado pela força magnética sobre as partículas, durante o deslocamento das mesmas na região .
Neste item, assuma que , e que é conhecida, enquanto que é desconhecida. Sabe-se também que as partículas, ao saírem da região , cruzam o eixo separadas por uma distância (veja figura). Nestas circunstâncias, calcule o valor da massa desconhecida , em função das grandezas conhecidas , , , e .
Ver solução completaQuestão 42
Seja uma superfície esférica dividida em duas semiesferas e por uma espira circular condutora ôhmica .
Sabendo-se a esfera está numa região onde há um campo magnético , que a espira tem uma resistência finita e desprezando qualquer efeito auto indutivo ou capacitivo, podemos afirmar que
o fluxo de através de é nulo.
o fluxo de através de é proporcional à corrente induzida na espira .
a circulação de em torno de é proporcional à corrente através de .
a taxa de variação temporal do fluxo de através de é proporcional à corrente induzida na espira .
a taxa de variação temporal do fluxo de através de é nula.
Ver solução completaQuestão 43
Um próton é lançado com velocidade constante numa região onde existe apenas um campo magnético uniforme , conforme a figura abaixo:

A velocidade e o campo magnético têm a mesma direção e mesmo sentido. Sendo e , podemos afirmar que o módulo da força magnética atuando no próton é:
Dado:
Ver solução completaQuestão 44
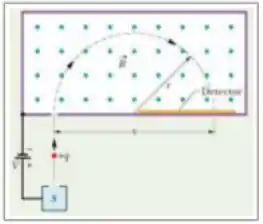
Considerando o espectrômetro de massa da figura, A) encontre a expressão literal para o raio em função dos valores de e ,supondo que a partícula esteja carregada com uma carga . B) Substitua , considere a massa e informe quanto vale .
Questão 45
Considere uma partícula de carga , a qual possui, num determinado instante, a velocidade . Nesse instante, a partícula está submetida a um campo elétrico e a um campo magnético . Qual é o vetor força resultante que age sobre a partícula? (Despreze efeitos gravitacionais)
(a)
(b)
(c)
(d)
(e) 0
Ver solução completaQuestão 46
Na figura abaixo, uma carga elétrica pontual , de massa , desloca-se ao longo do eixo com uma velocidade constante de módulo . Na origem do sistema de coordenadas (ponto ), tal partícula penetra numa região retangular de largura , onde existe um campo magnético uniforme que é perpendicular ao plano e que “entra” neste plano. Considere que o campo magnético é nulo fora da região indicada na figura. Depois de percorrer tal região de campo magnético, a partícula a abandona no ponto , localizado a uma altura em relação ao eixo . Nestas condições:
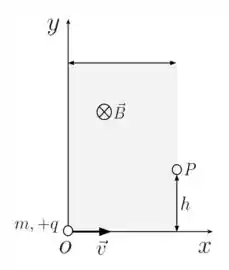
(a) Determine o vetor força magnética (em módulo, direção e sentido) que atua na partícula no ponto .
(b) Sabendo que a partícula entra na região de campo magnético em e sai em , calcule o módulo da velocidade para que isso aconteça, expressando-o em termos de , , , e .
(c) As energias cinéticas da partícula em e são dadas respectivamente por e . Determine .
Ver solução completaQuestão 47
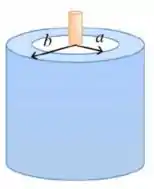
8) Um fio isolante muito longo (cor laranja) é colocado sobre o eixo de um cilindro metálico oco (cor azul), também muito longo. A densidade linear de carga do fio é , enquanto a densidade de carga por unidade de comprimento do cilindro é . (a) Qual a densidade de carga por unidade de comprimento nas superfícies interna e externa do cilindro, admitindo equilíbrio eletrostático?
Questão 48
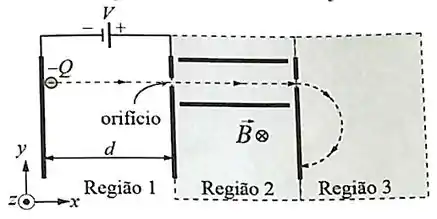
Um feixe de partículas com carga e massa é acelerado a partir do repouso através de uma diferença de potencial na região , e entra na região com uma gama de velocidade cuja direção é mostrada no diagrama. Há um campo magnético de módulo dirigido para dentro da página na região e um campo elétrico de módulo criado por placas paralelas carregadas na região 2. Com isso, algumas partículas passam pela região sem serem defletidas. Estas partículas entram na região , que contém somente um campo magnético de mesmo módulo e com a mesma orientação que na região . Determine:
(a) o módulo e a orientação do campo elétrico na região ;
(b) a velocidade com que as partículas entram na região ;
(c) o módulo da força magnética sobre as partículas na região ;
(d) o tempo de voo da partícula na região .
Ver solução completaQuestão 49
Em um espectrômetro de massa, um feixe de íons emitido por uma fonte atravessa uma região de campo magnético uniforme e estacionário, como mostrado na figura abaixo. Esse sistema é utilizado para determinar a quantidade de água pesada (, onde representa um átomo de deutério) que há na água do mar. Como resultado da ionização, separa-se apenas os íons , e , que são, então, acelerados de forma a entrarem na região de campo magnético com a mesma velocidade inicial. Sabendo que as massas dos átomos , e , valem 1, 2 e 16 u.m.a, respectivamente, e que a massa do elétron pode ser desprezada em confronto com as massas do próton e do nêutron, podemos afirmar que os íons coletados nos detectores 1 e 2, são, respectivamente:
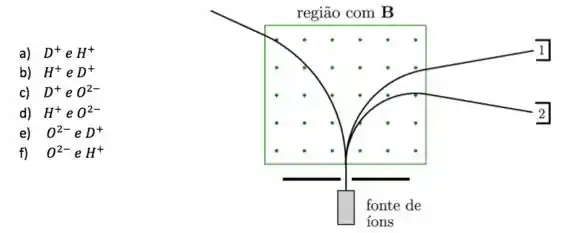
Questão 50
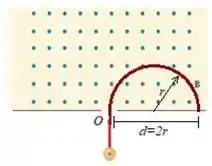
Uma partícula com carga , de massa , penetra, com uma velocidade , num campo magnético uniforme de intensidade através de um orifício existente no ponto de um anteparo. Determine a que distância do ponto a partícula incide no anteparo.
(a) .
(b)
(c)
(d)
(e)
Ver solução completaQuestão 51
Uma partícula de massa e carga , movendo-se no plano da página, é acelerada a partir do repouso através de uma diferença de potencial entre duas placas paralelas, como mostrado na região 1 da figura abaixo. A partícula passa por um orifício na placa da direita e penetra na região 2, onde há um campo magnético uniforme , perpendicular ao plano da página. Após descrever uma trajetória semicircular, a partícula atinge um detector. Em termos dos parâmetros dados e desprezando a ação da gravidade, determine:
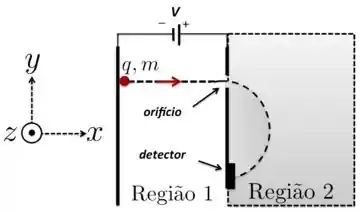
- O sinal da carga da partícula. Justifique.
- O sentido do campo magnético. Justifique.
- A velocidade da partícula ao entrar na região do campo.
- O vetor força exercida sobre a partícula pelo campo magnético no instante em que ela atinge o detector.
- A distância do orifício ao detector.
Questão 52
Uma partícula carregada entra em uma região de campo magnético constante que aponta ao longo do eixo de um sistema de coordenadas. Sua velocidade inicial aponta ao longo do eixo , de forma que ela entra em um movimento circular uniforme de raio . A seguir, a partícula é acelerada por um campo elétrico que aponta em uma direção contida no plano , de forma que sua energia cinética é quadruplicada. O campo elétrico então é removido e a partícula volta a executar um movimento circular uniforme. Nessas condições, o raio deste novo movimento vale:
Questão 53
A figura abaixo ilustra uma partícula que descreve uma trajetória semicircular ao entrar em uma região com campo magnético uniforme.
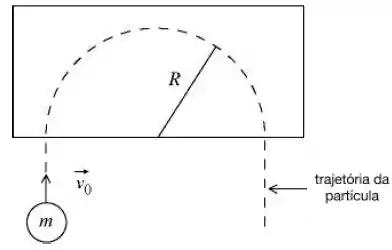
O raio da trajetória é e o módulo da velocidade da partícula ao entrar na região com campo magnético é . Sabendo que a partícula tem massa e carga , qual a magnitude e sentido do campo magnético?
, entrando na folha de papel.
, saindo na folha de papel.
, entrando na folha de papel.
, saindo na folha de papel.
, entrando na folha de papel.
Ver solução completaQuestão 54
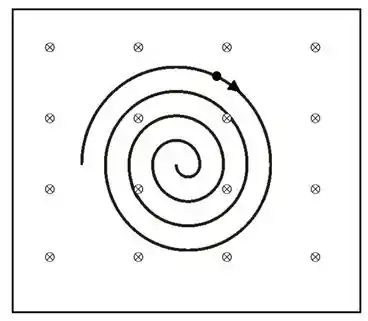
Um campo magnético uniforme tem seu vetor para dentro da página. Uma partícula carregada movimenta-se no plano da folha, seguindo uma espiral no sentido horário e raio decrescente, como é mostrado na figura. Uma explicação razoável é:
(a) a carga é positiva e desacelera
(b) a carga é negativa e desacelera
(c) a carga é positiva e acelera
(d) a carga é negativa e acelera
(e) nenhuma das anteriores
Questão 55
Um corpúsculo carregado com carga de passa com velocidade de na direção perpendicular a um campo de indução magnética e fica sujeito a uma força de . A intensidade desse campo é
Ver solução completaQuestão 57
Uma partícula carregada com carga positiva , massa e velocidade entra em uma região onde existe um campo magnético . O ângulo entre o vetor campo magnético e vetor velocidade da partícula é .
a) Calcule a força magnética atuando na partícula.
b) Calcule o raio do movimento da carga na presença do campo magnético.
Ver solução completaQuestão 58
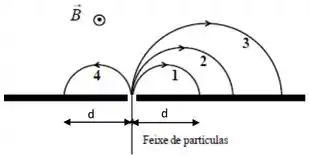
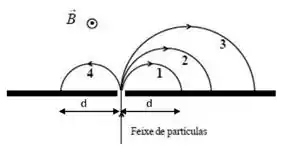
11 - Considere a trajetória das partículas 1, 2, 3 e 4 através de um espectrômetro de massa, conforme a figura. Considere também que todas as partículas entram no espectrômetro com a mesma velocidade e que possuam carga ou . Podemos afirmar que:
Questão 59
Um campo magnético uniforme e estacionário aponta para dentro do plano da página. Uma partícula carregada, movendo-se no plano da página, segue uma espiral no sentido horário de raio decrescente, como mostrado na figura abaixo. Uma explicação razoável para esta trajetória é:
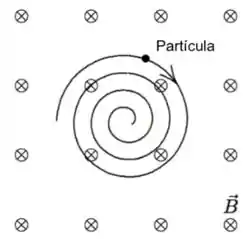
- A carga da partícula é positiva e sua velocidade está diminuindo.
- A carga da partícula é positiva e sua velocidade está aumentando.
- A carga da partícula é negativa e sua velocidade está aumentando.
- A carga da partícula é negativa e sua velocidade está diminuindo.
- Não há dados suficientes para dar uma explicação razoável.
Questão 60
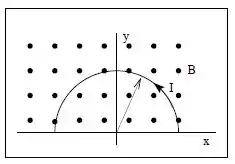
Um fio portador de corrente I está com a forma de uma semicircunferência de raio R, que está no plano . Há um campo magnético uniforme , perpendicular ao plano da espira, conforme a figura ao lado. Calcule a força que atua sobre a espira.
Questão 61
Um sistema a vácuo possui um pequeno vazamento de gás, cujos íons possuem carga e massa . Os íons escapam do vazamento na direção com velocidade de módulo . Para medir a intensidade do vazamento, aplica-se um campo magnético uniforme e estacionário de módulo e posicionamos um detector de partículas à direita da saída de gás no plano , conforme mostrado na figura abaixo.
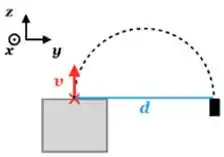
A que distância devemos posicionar o detector e que direção e sentido deve possuir o campo magnético para que os íons sejam detectados?
Escolha uma:
Ver solução completaQuestão 62
(Capítulo 28 – Problemas Adicionais – Exercício 74) Uma partícula de carga 2,0 C está se movendo na presença de um campo magnético uniforme. Em um certo instante, a velocidade da partícula é e a força magnética experimentada pela partícula é . As componentes e do campo magnético são iguais. Qual é o campo ?
Ver solução completaQuestão 63
Numa experiência de efeito Hall, uma tira condutora na forma de um paralelepípedo está disposta conforme indica a figura abaixo, sendo percorrida por uma corrente cujo sentido convencional está assinalado na figura. Sabe-se que o sinal das cargas dos portadores livres é positivo e que o potencial , na face de maior coordenada é maior que o potencial na parte inferior, , após o sistema atingir o regime estacionário. Indique a opção correta para uma possível direção de um campo magnético externo que provoca o efeito Hall.
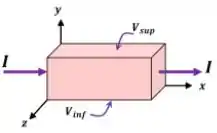
Escolha uma:
Ver solução completaQuestão 64
14) A câmara de bolhas representada na figura abaixo possui um campo magnético constante (estacionário e uniforme) , perpendicular à folha de papel. Uma partícula neutra, em repouso no centro da câmara, transforma-se (decai) em outras partículas, cujas trajetórias são mostradas na figura. Quanto à carga dessas partículas resultantes do decaimento, podemos afirmar que:
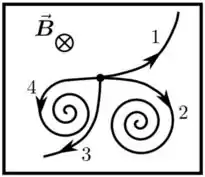
a) Todas as partículas , , e têm carga zero.
b) As partículas e têm cargas positivas, ao passo que as partículas e têm cargas negativas.
c) As partículas e têm cargas negativas, ao passo que as partículas e têm cargas positivas.
d) As partículas e têm cargas positivas, ao passo que as partículas e têm cargas negativas.
e) As partículas e têm cargas positivas, ao passo que as partículas e têm cargas negativas.
Ver solução completaQuestão 65
15) A figura abaixo representa um espectrômetro de massa, aparelho usado para medir a massa de íons. Um íon de massa '' (a ser determinada) e carga '' é produzido na fonte , em repouso, e acelerado pelo campo eletrostático associado a uma diferença de potencial . O íon entra em uma câmara de separação na qual existe um campo magnético constante (uniforme e estacionário), perpendicular à sua trajetória. Suponha que o íon atinja o detector em um ponto situado a uma distância do ponto de entrada da câmara. Qual é a massa do íon?
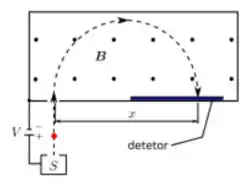
(a) .
(b) .
(c) .
(d) .
(e) .
Ver solução completaQuestão 66
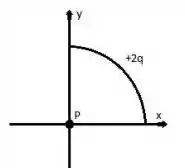
Uma barra fina (i.e. de espessura desprezível) de vidro na forma de um arco de circunferência de raio (conforme mostra a figura) possui uma carga uniformemente distribuída em seu comprimento.
a) Determine o módulo do campo elétrico no ponto , situado no centro do arco de circunferência.
b) Calcule o campo elétrico no mesmo ponto considerando agora que a carga está distribuída uniformemente ao longo de uma circunferência de raio .
Questão 67
2) Uma haste de comprimento gira em torno de uma extremidade a uma velocidade angular , mantida constante. A haste está imersa em um campo magnético uniforme , paralelo ao eixo de rotação da haste.
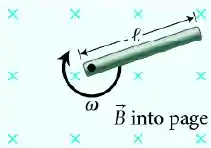
a) Em termos de e , qual diferença de potencial se desenvolve entre as duas extremidades da haste?
b) Qual extremidade da haste tem um potencial maior?
c) Quais são a direção, o sentido e o módulo do campo elétrico no interior da barra?
d) Qual das duas extremidades da barra possui excesso de carga positiva?
e) Se , e , qual é o valor da diferença de potencial do item (a)?
Ver solução completaQuestão 68
Uma partícula carregada com carga e massa é acelerada paralelamente ao eixo , no sentido de crescente, a partir do repouso, por uma diferença de potencial .
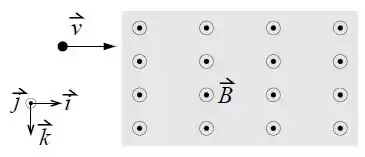
Determine o vetor velocidade final da partícula após a aceleração do potencial .
A partícula carregada adentra a seguir numa região de campo magnético uniforme . Determine o vetor força magnética que atua sobre a partícula em função de , , e .
Faça um esquema do movimento dessa partícula na região de campo . Calcule o raio da trajetória na região com campo magnético e o tempo gasto nesta região.
Ver solução completaQuestão 69
Um sistema a vácuo possui um pequeno vazamento de gás hélio, cujos íons possuem carga e massa . Os íons escapam do vazamento na direção com velocidade de módulo . Para medir a intensidade do vazamento, aplica-se um campo magnético uniforme e estacionário de módulo e posicionamos um detector de partículas à direita da saída de gás no plano , conforme mostrado na figura abaixo.
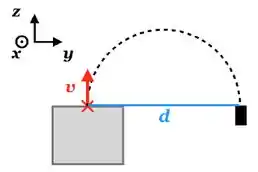
A que distância devemos posicionar o detector e que direção e sentido deve possuir o campo magnético para que os íons de hélio sejam detectados?
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 70
Um corpo de carga elétrica e massa penetra em um campo magnético de intensidade e movimenta-se com velocidade perpendicularmente a ; a trajetória é circular de raio . A partir de determinado instante, o corpo passa a descrever uma trajetória de maior raio. O fenômeno pode ser explicado por:
- Redução da massa do corpúsculo
- Aumento do módulo do campo
- Redução da carga
- Redução do módulo da velocidade do corpo
- Aumento da carga
Questão 71
Uma partícula de carga tem, em um dado instante, velocidade igual a . Nesse instante, a partícula está submetida a um campo elétrico dado por e a um campo magnético dado por , ambos uniformes e estacionários. Nessa situação, qual deve ser a razão para que a partícula se desloque em movimento retilíneo uniforme?
Questão 72
Um tubo de ensaio contém duas bolas de plástico, idênticas e uniformemente carregadas. As bolas estão em equilíbrio e separadas por uma distância , conforme mostrado na figura. Se a carga de cada bola for dobrada, a distância entre as bolas no tubo de ensaio se tornará (o atrito entre as bolas e o tubo pode ser desprezado):
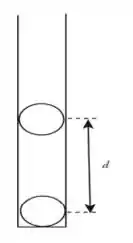
A)
B)
C)
D)
E)
Ver solução completaQuestão 73
As partículas puntiformes da figura, com carga cada uma, estão fixas formando um triângulo equilátero de lado e são ligadas por molas de constante elástica , inicialmente relaxadas. As partículas são então soltas, de modo que começam a se repelir. O triângulo se expande até que seu lado dobre, quando começa a se contrair de novo. Lembrando que a energia potencial elástica de uma mola é , onde é a deformação em relação à posição relaxada, calcule o valor de .

A)
B)
C)
D)
E)
Ver solução completaQuestão 74
(Cap 28 – Ex 2) Uma partícula com uma massa de e uma carga de se move em uma região onde existe um campo magnético uniforme e a aceleração da gravidade é . A velocidade da partícula é constante e igual a , perpendicular ao campo magnético. Qual é o campo magnético?
Ver solução completaQuestão 75
Três partículas se movem através de um campo magnético que aponta para fora da página. A figura mostra os caminhos seguidos pelas três partículas.
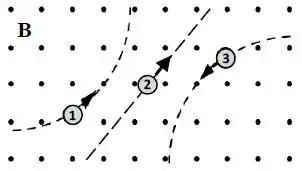
Assumindo que as partículas estão sujeitas somente a ação do campo magnético, qual das seguintes afirmações relacionadas com as partículas é verdadeira?
Todas as partículas são neutras.
A partícula 1 está carregada positivamente, a partículas 2 é positiva e a 3 é negativa.
A partícula 1 está carregada negativamente, a partículas 2 é neutra e a 3 é positiva.
A partícula 1 está carregada negativamente, a partículas 2 é neutra e a 3 é negativa.
A partícula 1 está carregada positivamente, a partículas 2 é neutra e a 3 é positiva
Ver solução completaQuestão 76
Numa placa transportando uma corrente uniforme cujo vetor densidade de corrente é dado por é aplicado um campo magnético também constante . Um voltímetro é ligado entre as superfícies superior e inferior da placa para medir a diferença de potencial como mostrado na figura abaixo. Sobre essa situação, podemos afirmar que, depois de atingido o equilíbrio,
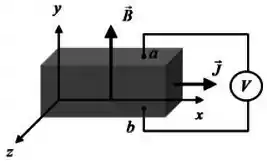
(a) se o portador da corrente for uma carga positiva, .
(b) se o portador da corrente for uma carga positiva, .
(c) se o portador da corrente for uma carga negativa, .
(d) se o portador da corrente for uma carga negativa, .
(e) independente do portador de carga.
Ver solução completaQuestão 77
Em qualquer ímã, os polos norte e sul tem:
- Forças semelhantes
- Forças diferentes
- Forças iguais
- Forças alternadas
- Forças variáveis
Questão 78
Três partículas viajam através de uma região do espaço onde o campo magnético horizontal aponta para fora da página, como mostrado na figura. A carga elétrica de cada uma das três partículas é, respectivamente,
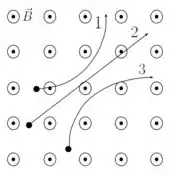
(a) 1 é neutro, 2 é negativo e 3 é positivo.
(b) 1 é neutro, 2 é positivo e 3 é negativo.
(c) 1 é positivo, 2 é neutro e 3 é negativo.
(d) 1 é positivo, 2 é negativo e 3 é neutro.
(e) 1 é negativo, 2 é neutro e 3 é positivo.
Ver solução completaQuestão 79
Considere a trajetória das partículas 1, 2, 3 e 4 através de um espectrômetro de massa, conforme ilustrado na figura. Considere também que todas as partículas entram no espectrômetro com a mesma velocidade e que as partículas possuem carga . Ordene em ordem decrescente estas partículas de acordo com suas massas.
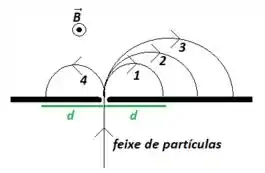
A) .
B) .
C) .
D) .
E) .
Ver solução completaQuestão 80
Três espiras circulares oscilam na presença de um campo magnético constante e uniforme, como ilustrado na figura. A espira 1 oscila de um lado para outro como um pêndulo, a espira 2 oscila em torno do seu eixo vertical e a espira 3 (presa na extremidade de uma mola) oscila para cima e para baixo. Em quais espiras haverá uma induzida?
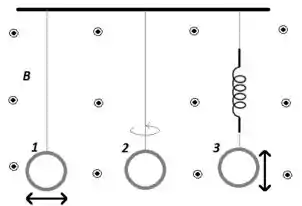
(A) Apenas a espira 1
(B) Apenas a espira 2
(C) Apenas a espira 3
(D) Espiras 1 e 2
(E) Espiras 1, 2 e 3
Ver solução completaQuestão 81
Uma fonte aplica uma com frequência de e valor de pico de em um circuito RLC em série que possui uma resistência de , uma capacitância de e um indutor de . Determine qual será o valor do pico de voltagem no indutor.
A)
B)
C)
D)
E)
Ver solução completaQuestão 82
Um fio retilíneo é curvado na forma mostrada na figura abaixo. Determine a força magnética resultante, que atua no fio quando por ele passa uma corrente elétrica , de acordo com o sentido mostrado na figura e na presença de um campo magnético.
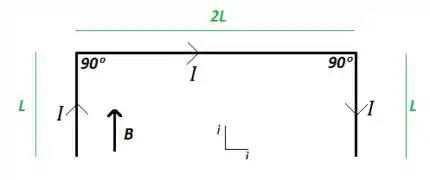
A) na direção
B) na direção
C) na direção
D) na direção
E) zero
Ver solução completaQuestão 83
Uma partícula carregada penetra em uma região de campo magnético uniforme e estacionário com velocidade inicial . Sendo o raio da trajetória helicoidal da partícula nessa região e a distância percorrida ao longo do eixo da hélice durante um período de revolução, podemos afirmar que a razão vale:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Ver solução completaQuestão 84
Em uma manobra arriscada, um avião executa um movimento de descida em uma trajetória retilínea com velocidade de módulo . Na região da manobra, o campo magnético terrestre é uniforme e tem módulo igual a . Na figura, representa o vetor normal às asas do avião, o campo magnético e a velocidade do avião. Esses três vetores são coplanares ao corpo do avião, sendo que as asas estão orientadas perpendicularmente à folha de papel. Sabendo que a envergadura (distância entre as extremidades das asas) do avião é , qual a diferença de potencial elétrico induzida entre as extremidades das asas?
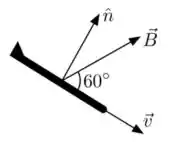
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 85
Uma partícula de carga elétrica penetra numa região de campo magnético uniforme com uma velocidade . Observe que , e denotam os vetores unitários ao longo dos eixos , e , respectivamente. Sabe-se que a massa da partícula em questão é . Nestas circunstâncias, calcule:
- O vetor força magnética que atua sobre a partícula.
- O cosseno do ângulo formado entre os vetores e .
- O deslocamento da partícula ao longo da direção paralela ao campo magnético quando a mesma completa um período de seu movimento de rotação.
- O raio da trajetória seguida pela partícula.
Questão 86
Duas esferas idênticas, cada uma com massa , são suspensas por fios ideais e isolantes de comprimento , como indicado na figura abaixo. Elas possuem cargas de mesmo módulo e sinais opostos e estão sob a ação de um campo elétrico uniforme , de direção horizontal e intensidade desconhecida, e do campo gravitacional . Quando o sistema está em equilíbrio, o ângulo que os fios fazem com a vertical vale . Nessas condições, determine:
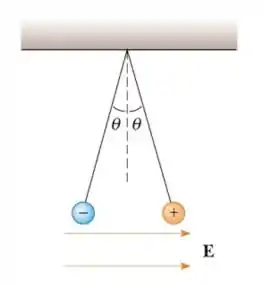
- A tensão no fio
Questão 87
Duas esferas idênticas, cada uma com massa , são suspensas por fios ideais e isolantes de comprimento , como indicado na figura abaixo. Elas possuem cargas de mesmo módulo e sinais opostos e estão sob a ação de um campo elétrico uniforme , de direção horizontal e intensidade desconhecida, e do campo gravitacional . Quando o sistema está em equilíbrio, o ângulo que os fios fazem com a vertical vale . Nessas condições, determine:
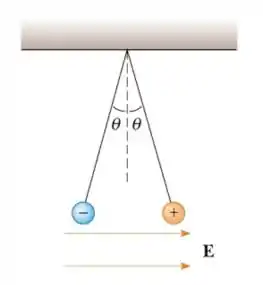
b) A intensidade do campo elétrico.
Ver solução completaQuestão 88
Considerando o espectrômetro de massa da figura, A) encontre a expressão literal para o raio em função dos valores de e ,supondo que a partícula esteja carregada com uma carga . B) Substitua , considere a massa e informe quanto vale .
Questão 89
Uma partícula alfa com carga e massa está se movendo com velocidade quando entra em um campo magnético uniforme fazendo um ângulo reto com a sua direção de movimento.
Um dêuteron de carga e massa também entra no campo na mesma direção e com a mesma velocidade.
Calcule a diferença entre os raios das trajetórias da partícula alfa e do dêuteron na região do campo magnético (sabendo-se que e )
Ver solução completa
Questão 90
Um campo elétrico , onde , dado em , , dada e são constantes, e é o tempo em , é aplicado no interior de uma região cilíndrica de raio que possui seu eixo de simetria orientado na direção . Seja a distância radial ao eixo de simetria da região cilíndrica, é dado em .
(a) Calcule o vetor campo magnético para .
(b) Calcule o vetor campo magnético para.
Ver solução completaQuestão 91
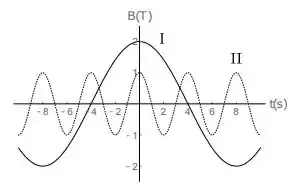
Considere duas situações: na primeira, uma espira circular de área é atravessada perpendicularmente por um campo magnético uniforme que oscila periodicamente no tempo de acordo com a curva I na figura abaixo (curva cheia), e na segunda situação a mesma espira é atravessada perpendicularmente por um campo magnético uniforme oscilante descrito pela curva II (curva pontilhada). Sejam e os valores máximos da força eletromotriz induzida na espira nas situações e , respectivamente. Nessas condições, podemos afirmar que a razão vale:
Questão 92
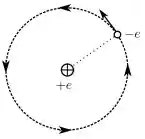
Em um modelo clássico para o átomo de Hidrogênio, um elétron descreve um movimento circular uniforme em torno de um próton, fixado na origem de um sistema de coordenadas. O sentido da trajetória do elétron é mostrado na figura abaixo. Suponha que a corrente associada ao movimento do elétron pode ser tratada como estacionária. Sobre essa corrente e o campo magnético produzido por ela na posição do próton, podemos afirmar que:
- A corrente tem sentido horário e o campo aponta para dentro do plano do papel.
- A corrente tem sentido anti-horário e o campo aponta para dentro do plano do papel.
- A corrente tem sentido horário e o campo aponta para fora do plano do papel.
- A corrente tem sentido anti-horário e o campo aponta para fora do plano do papel.
- A corrente tem sentido anti-horário e o campo é nulo.
- A corrente tem sentido horário e o campo é nulo.
Questão 93
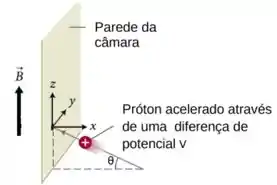
Um próton de massa e carga é acelerado através de uma diferença de potencial , e disparado na direção de uma câmara, como mostrado na figura ao lado. Na figura, a câmara é toda a região à esquerda da parede. Não há campo elétrico na câmara, mas há um campo magnético uniforme na direção positiva. O próton entra na câmara através de um furo na parede, formando um ângulo com o eixo . Considere este ponto de entrada como a origem do sistema de coordenadas . Determine as coordenadas do local, na parede da câmara, que o próton irá atingir, pelo lado de dentro, após interação com o campo magnético. Dica: O próton fará um movimento do tipo espiral dentro da câmara.
Questão 94
No esquema da figura 1 estão representadas uma esfera compacta de material isolante de raio e uma casca condutora, concêntrica com ela, de raio interno e raio externo . A esfera isolante está carregada uniformemente com densidade volumétrica de carga . A casca condutora tem carga total nula.
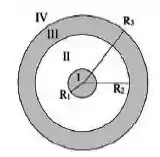
- Calcule o vetor campo elétrico nas regiões .
Questão 95
Um próton e uma partícula alfa (formada por dois prótons e dois nêutrons) penetram em uma região de campo magnético uniforme, de forma que suas velocidades iniciais são idênticas e perpendiculares à direção do campo.
Considerando que a massa do próton é aproximadamente igual à massa do nêutron, a razão entre os raios das trajetórias circulares do próton e da partícula alfa , nessa região, vale:
4;
2;
1;
½;
¼;
Ver solução completaQuestão 96
Considere quatro cargas pontuais colocadas nos vértices de um quadrado de lado como mostrado na figura abaixo.
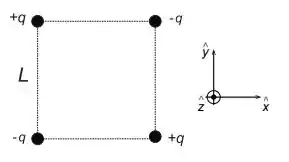
Calcule:
A força sobre a carga situada no vértice superior direito.
Ver solução completaQuestão 97
Uma barra metálica de comprimento , massa e resistência total está sobre trilhos metálicos sem atrito, inclinados em um ângulo em relação à horizontal. Os trilhos possuem resistência desprezível. Um campo magnético uniforme de módulo está orientado para baixo, como indicado na figura abaixo. A barra é liberada a partir do repouso e desliza para baixo sobre os trilhos.
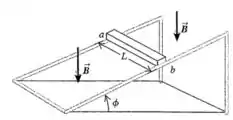
d) Depois que a velocidade terminal da barra for atingida, qual será a taxa de conversão de energia elétrica em energia térmica na barra?
e) Depois que a velocidade terminal da barra for atingida, qual é a taxa do trabalho realizado pela força da gravidade? Compare a sua resposta com o que foi encontrado no item (d).
Ver solução completaQuestão 98
Um fio infinito com densidade linear de carga positiva está posicionado a uma distância da ponta de um bastão de comprimento com carga positiva uniformemente distribuída ao longo de toda sua extensão, conforme mostrado na figura abaixo. Calcule o módulo da força de repulsão exercida sobre o bastão.
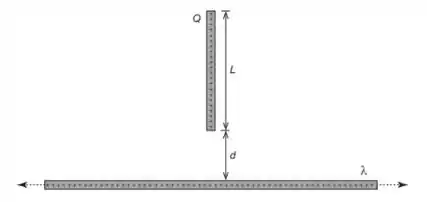
Questão 99
Uma carga pontual positiva está posicionada a uma distância da ponta de um bastão de comprimento com carga positiva uniformemente distribuída ao longo de toda sua extensão, conforme mostrado na figura abaixo. Calcule o módulo da força de repulsão exercida sobre a carga .
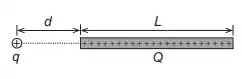
Questão 100
Considere um capacitor formado por duas placas paralelas quadradas de lado , colocadas a uma distância uma da outra, sendo . Calcule:
A diferença de potencial entre as placas.
Ver solução completaQuestão 101
Uma esfera oca de raio interno e raio externo é feita de um material de resistividade . As paredes internas e externa dessa esfera são metalizadas. Supondo que seja muito maior que a resistividade do metal depositado, calcule a resistência elétrica entre as paredes interna e externa.
Ver solução completaQuestão 102
Um cilindro oco de comprimento raio interno e raio externo é feito de um material de resistividade . As paredes internas e externa desse cilindro são metalizadas. Supondo que seja muito maior que a resistividade do metal depositado, calcule a resistência elétrica entre as paredes interna e externa.
Ver solução completaQuestão 103
Considere quatro cargas pontuais colocadas nos vértices de um quadrado de lado como mostrado na figura abaixo.
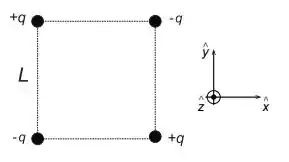
Calcule:
A força sobre a carga situada no vértice superior direito.
Ver solução completaQuestão 104
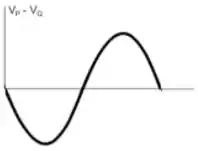
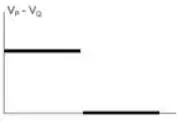
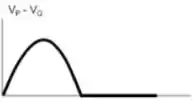
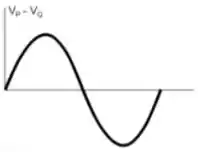
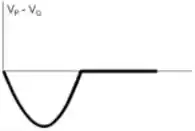
A figura mostra uma pequena barra condutora , contida no plano , que tem sua extremidade pivotada ao eixo , de forma a poder girar livremente em torno dele com velocidade angular de módulo constante . Um campo magnético constante (estacionário e uniforme), perpendicular ao plano de seu movimento e orientado no sentido negativo do eixo , ocupa o semi-espaço superior , como mostrado na figura. Sabendo que no instante inicial , qual dos gráficos abaixo melhor representa a diferença de potencial , como função do tempo, a cada volta completa em torno do eixo?
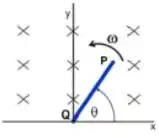
Escolha uma:
. 
. 
. 
. 
. 
. 
Questão 105
Considere uma fita retangular, feita de cobre, por onde passa uma corrente estacionária de intensidade com o sentido indicado na figura abaixo. A fita está sujeita à ação de um campo magnético constante que aponta para fora do plano da fita. Considere os pontos , e indicados na figura. Sabendo que os portadores de carga no cobre são os elétrons, podemos afirmar que os potenciais elétricos nestes pontos, dados por , e , respectivamente, satisfazem:
Questão 106
10 - Elétrons (massa , carga ) são acelerados do repouso através de uma diferença de potencial e são então desviados por um campo magnético que é perpendicular à sua velocidade. O raio da trajetória do elétron resultante é:
- Nenhuma das anteriores.
Questão 107
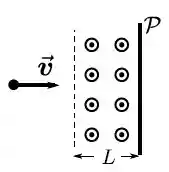
A figura mostra um campo magnético constante (uniforme e estacionário) preenchendo uma faixa retangular de altura muito grande e largura . Se uma partícula de massa e carga elétrica , com velocidade , incidir perpendicularmente a tal faixa, qual o módulo máximo que sua velocidade pode ter para que ela não colida com o painel ?
Questão 108
A figura abaixo ilustra diferentes partículas sendo injetadas por uma abertura no ponto em uma região com um campo magnético uniforme perpendicular à velocidade das partículas, que é a mesma para todas as partículas. O campo é perpendicular à página e aponta para “fora” dela. As patículas descrevem as trajetórias identificadas por I, II, III e IV.
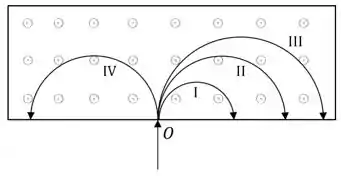
Quais das afirmativas a seguir são verdadeiras?
1. A partícula da trajetória II possui carga negativa e a da trajetória IV possui carga positiva.
2. Supondo que todas as partículas tenham mesma carga, a da trajetória II tem maior massa que a da trajetória I.
3. Supondo que todas as patículas tenham mesma massa, a da trajetória III tem maior carga que a da trajetória II.
4. Se o módulo do campo magnético B fosse aumentado, todas as trajetórias teriam um raio menor.
a) 2 e 4
b) 1, 3 e 4
c) 1, 2 e 3
d) 1 e 2
e) 3 e 4
Ver solução completaQuestão 109
Dentre as afirmações que seguem, diga qual/is é/são incorreta/s:
I- O campo magnético não realiza trabalho, porque a força magnética é sempre perpendicular à velocidade de uma partícula carregada.
II- O campo magnético altera a direção e o módulo da velocidade de uma partícula carregada
III-A energia cinética de uma partícula carregada num campo magnético permanece constante.
(a) Apenas I
(b) Apenas II
(c) Apenas III
(d) Apenas I e III
(e) Apenas II e III
Ver solução completaQuestão 110
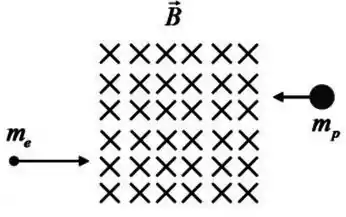
Um próton de massa , carga e velocidade com módulo igual a , junto a um elétron de massa , carga e velocidade com módulo entram numa região de campo magnético constante (uniforme e estacionário) de módulo , como mostrado na figura abaixo. Determine a razão entre o raio da orbita do próton () e o raio da órbita do elétron ()
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 111
Uma carga positiva move-se para direita e sofre a ação de uma força magnética na direção vertical com orientação para cima. Em qual sentido deve apontar o campo magnético?
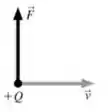
Questão 112
Uma espira transporta corrente em sentido horário (vista de cima da espira) está posicionada de modo que seu centro encontra-se exatamente acima do centro de outra espira que é percorrida por uma corrente em sentido oposto, isto é, em sentido anti-horário (vista de cima da espira) como mostra a figura. Em que sentido apontará a força magnética exercida sobre a espira superior?
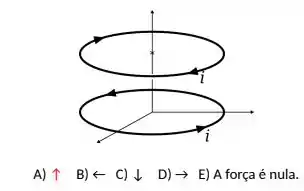
Questão 113
Em uma manobra arriscada, um avião executa um movimento de descida em uma trajetória retilínea com velocidade de módulo . Na região da manobra, o campo magnético terrestre é uniforme e tem módulo igual a . Na figura ao lado, representa o vetor normal às asas do avião, o campo magnético e a velocidade do avião. Esses três vetores são coplanares ao corpo do avião, sendo que as asas estão orientadas perpendicularmente à folha de papel. Sabendo que a envergadura (distância entre as extremidades das asas) do avião é , qual a diferença de potencial elétrico induzido entre as extremidades das asas?
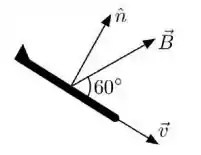
Questão 114
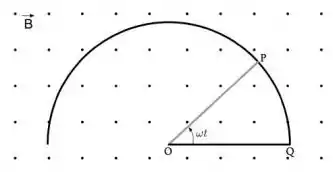
A figura mostra uma região com campo magnético uniforme e constante, perpendicular à folha de papel e saindo da mesma, onde foi colocado um trilho condutor de resistência nula, formado por um trecho semicircular e o segmento retilíneo OQ. O segmento OP representa uma haste condutora de resistência que pode girar livremente em torno do ponto O, fazendo contato elétrico com o trilho através dos pontos O e P. Ao fazer a haste móvel girar com velocidade angular constante , no sentido anti-horário, o que se pode dizer sobre a corrente elétrica que circula no circuito OQP?
- Uma corrente elétrica constante circula no sentido horário.
- Uma corrente elétrica constante circula no sentido anti-horário.
- Uma corrente elétrica que aumenta no tempo circula no sentido horário.
- Uma corrente elétrica que aumenta no tempo circula no sentido anti-horário.
- Não circula corrente elétrica no circuito nessa situação.
Questão 115
Um feixe de elétrons viaja a uma velocidade de . Qual deve ser a intensidade do campo magnético aplicado perpendicularmente ao feixe para que este se mova em uma trajetória circular de raio ?
Questão 116
Uma partícula de carga se desloca inicialmente com velocidade constante . Num dado instante, ela entra através da abertura em uma caixa que é dividida em três regiões chamadas I, II e III, como mostra a figura abaixo. Nas regiões I e III a partícula é submetida somente a um campo magnético constante de mesmo módulo, enquanto na região II ela é submetida somente a um campo elétrico constante. Observa-se então que a partícula tem a trajetória indicada e sai da caixa através da abertura A2. Considerando que todo o movimento dela se dá no plano XY, qual é o sentido dos campos nas regiões I, II e III, respectivamente?
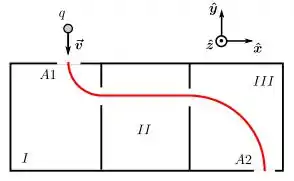
Questão 117
Dois fios retilíneos, paralelos, muito longos, separados por uma distância , são percorridos por correntes estacionárias de sentidos opostos e mesma intensidade , conforme mostra a figura. Um terceiro fio, circular, de raio , é colocado entre os primeiros fios, Qual devem ser a intensidade e o sentido da corrente que esse último fio deve portar para que o campo magnético resultante no seu centro seja nulo?
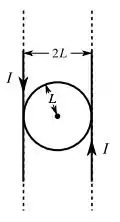
- e horário.
- e anti-horário.
- e horário.
- e anti-horário.
- e horário.
- e anti-horário.
- A corrente no fio circular deve ser zero.
Questão 118
Considere uma partícula de carga e velocidade, imersa num campo magnético uniforme e estacionário . Qual é a força magnética sofrida por essa partícula?
Questão 119
A figura mostra um íon de massa e carga que é acelerado, a partir do repouso, pela aplicação de uma diferença de potencial entre sua posição inicial e o orifício que existe na placa metálica superior.
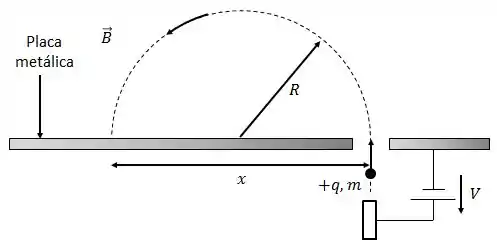
Na região acima desta placa é aplicado um campo magnético de intensidade , uniforme e perpendicular à folha. Este campo faz a trajetória do íon descrever um semicírculo, indo atingir a placa a uma distância .
Em termos de , , e , calcule:
- A velocidade do íon ao travessar o orifício da placa;
- A distância entre o ponto em que o íon passa no orifício e o ponto em que ele colide com a placa;
- Qual o sentido do vetor ? Justifique, fazendo representação vetorial na figura;
Questão 120
A figura ilustra uma partícula de carga elétrica negativa (), que penetra com velocidade em uma região do espaço onde existe um campo magnético uniforme (área hachurada na figura). Sabe-se que o vetor é perpendicular ao vetor . Com relação a tal situação, assinale a alternativa que indica (i) a trajetória da carga elétrica (indicada pelas linhas tracejadas) e (ii) o módulo da força magnética, , que atua na carga durante seu movimento na região onde atua o campo magnético .
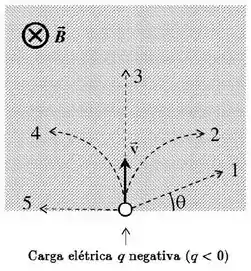
(a) (i) trajetória 1; (ii)
(b) (i) trajetória 2; (ii)
(c) (i) trajetória 3; (ii)
(d) (i) trajetória 4; (ii)
(e) (i) trajetória 5; (ii)
Ver solução completaQuestão 121
Uma partícula carregada com carga se desloca com velocidade constante . Ela então entra através da abertura numa caixa que é dividida em duas partes (chamadas 1 e 2), onde podem ser aplicados campos magnéticos uniformes e estacionários em cada uma delas.
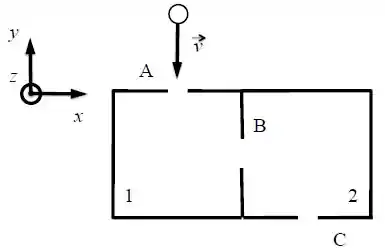
Na placa que separa as duas metades existe uma abertura para permitir a passagem da partícula. Observa-se que em seguida a partícula sai da caixa através da abertura C com a mesma velocidade .
Sejam e os módulos do campo magnético nas partes 1 e 2, respectivamente, com e . Dentre as opções abaixo, qual delas melhor descreve os vetores campo magnético nas duas partes da caixa?
e ;
e ;
e ;
e ;
e ;
Ver solução completaQuestão 122
Uma partícula carregada movimenta-se através de um campo magnético uniforme. Considere as seguintes afirmações a respeito do campo magnético:
- Ele exerce uma força que é perpendicular à direção do movimento da partícula;
- Ele exerce uma força que tem a direção do movimento;
- Ele exerce uma força paralela ao campo;
- Ele aumenta a energia cinética da partícula;
- Ele não altera o módulo do momento linear da partícula;
Qual(is) é(são) as informações verdadeira(s)?
- Nenhuma delas;
- II e IV;
- Apenas I;
- Apenas III;
- I e V;
Questão 123
Na figura abaixo, uma carga elétrica pontual (com ), de massa , desloca-se ao longo do eixo com uma velocidade constante de módulo .
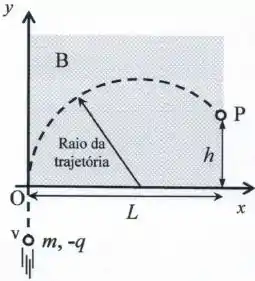
Na origem do sistema de coordenadas (ponto ), tal partícula penetra numa região retangular de largura , onde existe um campo magnético uniforme que é perpendicular ao plano .
Considere que o campo magnético é nulo fora da região hachurada indicada na figura. Depois de percorrer uma trajetória circular (curva tracejada na figura), a partícula abandona a região de campo magnético no ponto , localizado a uma altura em relação ao eixo .
Determine o sentido do campo magnético (entrando ou saindo do plano ). Justifique brevemente sua resposta.
Determine o módulo da velocidade da partícula no ponto . Justifique brevemente sua resposta.
Calcule o raio da trajetória em função de e .
Calcule a altura em função de e .
Ver solução completaQuestão 124
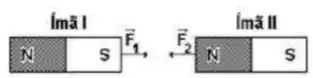
Dois ímãs estão dispostos em cima de uma mesa de madeira, conforme a figura anterior. é a força que o íma II exerce sobre o ímã I, enquanto que este exerce uma força sobre o ímã II. Considerando e representam os módulos dessas duas forças, podemos afirmar que:
- , pois o polo sul
- , pois o polo norte atrai o polo sul
- s forças são diferentes, embora não se possa afirmar qual é maior
Questão 125
Quando um ímã em forma de barra é partido ao meio, observa-se que:
- Os corpos deixam de possuir propriedades magnéticas
- Obtemos ímãs unipolares
- Um deles deixa de possuir propriedades magnéticas
- Damos origem a dois novos ímãs
Questão 126
Campo Magnético pode ser entendido de forma qualitativa como a influencia que um material magnético exerce ao seu redor. Assim, como associamos a influência elétrica ao campo elétrico, associaremos a influência magnética ao campo magnético.
Levando em conta o exposto anteriormente, determine a intensidade da força magnética que atua sobre a carga positiva de , atravessando o vácuo com velocidade igual a e que forma um ângulo de com o vetor campo magnético de intensidade igual a
Ver solução completaQuestão 127
2.5) Considere a figura abaixo, onde um íon positivo de massa e carga possui uma
velocidade em uma região onde há um campo magnético entrando no papel.
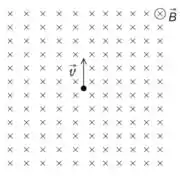
(a) Desenhe a trajetória do íon na figura.
Ver solução completaQuestão 128
2.6) Considere um toróide de raio interno e raio externo . Sabendo que o toróide possui
espiras, e que por elas circula uma corrente , calcule o campo magnético no interior do
toróide, em um ponto a uma distância do seu centro.
Ver solução completaQuestão 129
Um elétron se movimenta em uma trajetória retilínea com velocidade na presença de um campo elétrico e de um campo magnético constantes. A componente da velocidade do elétron é:
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 130
2.5) Considere a figura abaixo, onde um íon positivo de massa e carga possui uma
velocidade em uma região onde há um campo magnético entrando no papel.
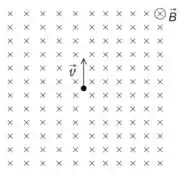
(b) Determine o raio da trajetória.
Ver solução completaQuestão 131
3.1) Um anel retangular de largura e comprimento , contendo uma resistência , tem
seu plano orientado paralelamente ao plano do papel. Este anel é inicialmente atravessado
perpendicularmente por um campo magnético entrando no plano do papel, ao longo de
toda sua área. O campo é uniforme e de módulo constante . O anel move-se para fora
da região do campo, na direção paralela ao plano do papel, no sentido para a direita, como
indicado na figura abaixo. Sabendo que o deslocamento (veja figura) varia com o tempo
na forma , determine:
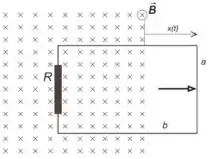
(c) A quantidade de calor dissipada pelo resistor por intervalo de tempo.
Ver solução completaQuestão 132
2.9) Um cilindro fino de comprimento gira com frequência angular em torno de um eixo
transversal que atravessa o ponto médio entre as suas extremidades. O cilindro é feito de
material isolante e possui uma densidade linear de carga uniformemente distribuída ao
longo de sua extensão. Calcule o momento de dipolo magnético gerado pela rotação.
Ver solução completaQuestão 133
3.1) Um anel retangular de largura e comprimento , contendo uma resistência , tem
seu plano orientado paralelamente ao plano do papel. Este anel é inicialmente atravessado
perpendicularmente por um campo magnético entrando no plano do papel, ao longo de
toda sua área. O campo é uniforme e de módulo constante . O anel move-se para fora
da região do campo, na direção paralela ao plano do papel, no sentido para a direita, como
indicado na figura abaixo. Sabendo que o deslocamento (veja figura) varia com o tempo
na forma , determine:
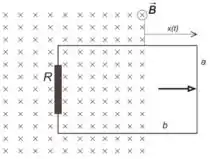
(a) O sentido da corrente induzida no anel (horário ou anti-horário de acordo com a figura).
Ver solução completaQuestão 134
3.1) Um anel retangular de largura e comprimento , contendo uma resistência , tem
seu plano orientado paralelamente ao plano do papel. Este anel é inicialmente atravessado
perpendicularmente por um campo magnético entrando no plano do papel, ao longo de
toda sua área. O campo é uniforme e de módulo constante . O anel move-se para fora
da região do campo, na direção paralela ao plano do papel, no sentido para a direita, como
indicado na figura abaixo. Sabendo que o deslocamento (veja figura) varia com o tempo
na forma , determine:
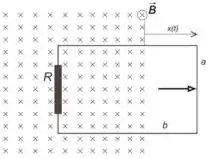
(b) A força eletromotriz induzida no anel em função do tempo .
Ver solução completaQuestão 135
3.2) Um anel retangular de largura e comprimento , contendo uma resistência , está
orientado com seu plano ortogonal a um campo magnético entrando no plano do papel.
O campo é uniforme e de módulo constante . O anel move-se para dentro da região do campo, na direção paralela ao plano do papel, no sentido para a esquerda, como indicado na
figura do problema. Sabendo que o deslocamento (veja figura abaixo) varia com o tempo
como , determine:
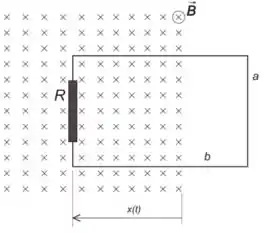
(a) O sentido da corrente induzida no anel (horário ou anti-horário de acordo com a figura).
Ver solução completaQuestão 136
3.2) Um anel retangular de largura e comprimento , contendo uma resistência , está
orientado com seu plano ortogonal a um campo magnético entrando no plano do papel.
O campo é uniforme e de módulo constante . O anel move-se para dentro da região do campo, na direção paralela ao plano do papel, no sentido para a esquerda, como indicado na
figura do problema. Sabendo que o deslocamento (veja figura abaixo) varia com o tempo
como , determine:
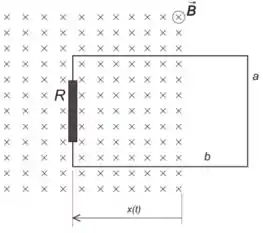
(b) O valor da corrente induzida no anel em função do tempo .
Ver solução completaQuestão 137
3.2) Um anel retangular de largura e comprimento , contendo uma resistência , está
orientado com seu plano ortogonal a um campo magnético entrando no plano do papel.
O campo é uniforme e de módulo constante . O anel move-se para dentro da região do campo, na direção paralela ao plano do papel, no sentido para a esquerda, como indicado na
figura do problema. Sabendo que o deslocamento (veja figura abaixo) varia com o tempo
como , determine:
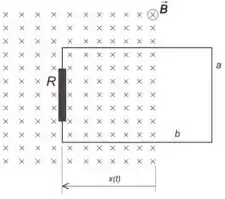
(c) A quantidade de calor dissipada pelo anel em um intervalo de tempo .
Ver solução completaQuestão 138
3.3) Uma bobina de espiras, raio , resistência R, e comprimento é coaxial com
outra bobina de mesmo comprimento , mas com espiras e raio . Através da
bobina passa uma corrente que varia com o tempo como . Calcule:
(b) A energia dissipada na bobina no intervalo de tempo entre e .
Ver solução completaQuestão 139
3.4) Uma bobina de espiras, raio , resistência , e comprimento é coaxial com
outra bobina de mesmo comprimento , mas com espiras e raio . Através da bobina passa uma corrente que varia com o tempo como . Calcule:
(a) A força eletromotriz induzida na bobina em função do tempo.
Ver solução completaQuestão 140
3.4) Uma bobina de espiras, raio , resistência , e comprimento é coaxial com
outra bobina de mesmo comprimento , mas com espiras e raio . Através da bobina passa uma corrente que varia com o tempo como . Calcule:
(b) A taxa com a qual a energia é dissipada na bobina , em função do tempo.
Ver solução completaQuestão 141
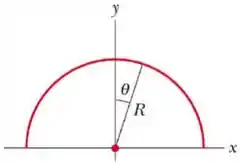
4) A figura ao lado mostra um fio não condutor carregado, em forma de semicírculo. Obtenha o vetor campo elétrico no centro, admitindo: (b) que a densidade de carga varia segundo , onde é constante.
Questão 142
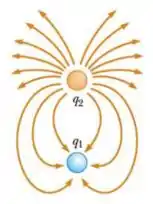
2) A figura ao lado mostra as linhas de campo geradas por duas cargas puntiformes, e .
(b) Qual a razão entre as cargas, , em valor absoluto?
Questão 143
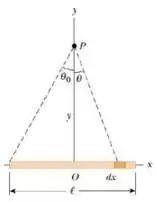
3) Um fio isolante uniformemente carregado tem comprimento e densidade de carga uniforme , como mostrado na figura ao lado. O ponto se situa à distância do fio, verticalmente sobre seu centro. (a) Mostre que o campo elétrico em é dado por
Dica: Explore a relação e integre sobre a variável angular.
(b) Obtenha o campo elétrico para do fio infinito, , a partir do resultado do item (a).
Questão 144
4) A figura ao lado mostra um fio não condutor carregado, em forma de semicírculo. Obtenha o vetor campo elétrico no centro, admitindo: (a) que o fio é uniformemente carregado com densidade
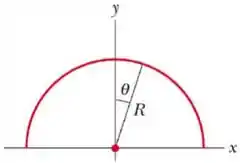
Questão 145
7) Duas esferas condutoras idênticas são colocadas próximas uma da outra. Uma das esferas tem carga elétrica , enquanto a outra tem carga , onde . Observa-se que apesar das cargas de mesmo sinal, as duas esferas se atraem. Explique por que isso pode acontecer.
Ver solução completaQuestão 146
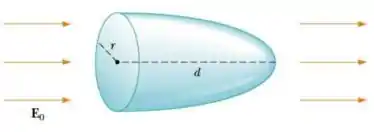
5) Em uma região do espaço existe um campo elétrico uniforme de magnitude . Calcule o fluxo do campo elétrico através da superfície paraboloide indicada na figura, notando que o eixo de simetria do paraboloide é paralelo ao campo elétrico.
Questão 147
6) Considere um fio muito longo, feito de material isolante e uniformemente carregado com densidade . Obtenha o fluxo do campo elétrico através de uma superfície Gaussiana esférica de raio e centrada no ponto (ver figura), em duas situações: (a) , e (b) .
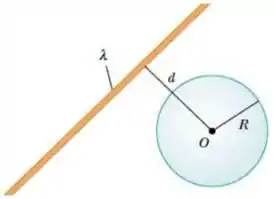
Questão 148
8) Um fio isolante muito longo (cor laranja) é colocado sobre o eixo de um cilindro metálico oco (cor azul), também muito longo. A densidade linear de carga do fio é , enquanto a densidade de carga por unidade de comprimento do cilindro é . (b) O campo elétrico no exterior do cilindro à distância de seu eixo.
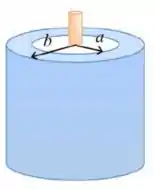
Questão 149
8) Um fio isolante muito longo (cor laranja) é colocado sobre o eixo de um cilindro metálico oco (cor azul), também muito longo. A densidade linear de carga do fio é , enquanto a densidade de carga por unidade de comprimento do cilindro é . (c) Calcule também o campo elétrico nas regiões , e .
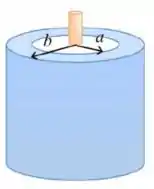
Questão 150
9) Uma esfera de raio não condutora tem carga uniformemente distribuída em seu volume, com densidade . Todavia, a esfera não é completamente maciça, pois há uma cavidade esférica de raio , como indicado na figura. Calcule o campo elétrico no interior da cavidade. Dica: A cavidade pode ser descrita pela superposição de densidades de carga positiva e negativa. Obtenha o campo gerado por cada densidade e explore o Princípio de Superposição.
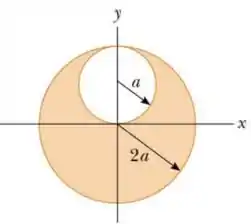
Questão 151
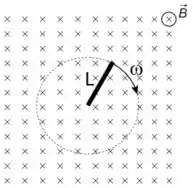
3.5) Uma barra metálica de comprimento ocupa uma região onde há um campo magnético
uniforme e estático . A barra gira com velocidade angular em torno de um ponto fixo
em uma das suas extremidades, em um plano perpendicular ao campo (ver figura). Calcule
a força eletromotriz induzida na barra.
Questão 152
3.6) Uma barra de comprimento está orientada em direção perpendicular a um fio longo
no qual corre uma corrente . A extremidade da barra mais próxima ao fio está a uma
distância do fio e move-se com velocidade paralela ao fio (ver figura). Calcule a diferença
de potencial entre as extremidades da barra.

Questão 153
3.7) Um solenoide longo de raio cria um campo magnético homogêneo em seu interior, o qual varia no tempo na forma , onde é uma constante. Calcule a intensidade do
campo elétrico induzido a uma distância do eixo do solenoide e desenhe as linhas de força
do campo elétrico induzido.
Ver solução completaQuestão 154
3.8) Um fio metálico cilíndrico de raio é envolvido por uma capa metálica cilíndrica de raio
. Um plástico isolante e não magnético preenche o espaço entre o fio e a capa (podemos
tratá-lo como vácuo). Uma corrente de mesma intensidade se propaga no fio e na capa
em sentidos opostos. Calcule a autoindutância por unidade de comprimento do cabo.
Ver solução completa