Exercícios de Propagação das Ondas Eletromagnéticas - Lista de Exercícios Resolvida

É conhecido que um campo elétrico de uma onda plana eletromagnética propagando-se num meio dielétrico (onde ) é dado por

onde , e .

Obs: As relações e as equações para uma onda eletromagnética num meio dielétrico são as mesmas que para uma onda eletromagnética no vácuo, substituindo apenas nas relações a velocidade da onda eletromagnética no vácuo pela velocidade da onda eletromagnética no meio dielétrico.

1. Qual é o vetor unitário da direção propagação da onda?
2. Calcule o vetor campo magnético da onda.

Uma onda eletromagnética possui módulo do campo magnético e frequência , sabendo que o vetor de propagação da onda está no mesmo sentido e é proporcional a , escreva uma expressão para o vetor campo magnético e determine o comprimento de onda.

Usando a notação complexa, some os campos elétricos abaixo:

Sendo e

Uma onda eletromagnética senoidal plana se propagando no ar possui comprimento de onda igual a e a amplitude do campo elétrico é igual a .

Dê as suas respostas em valores numéricos.

1. Qual é a frequência desta onda?
2. Sabendo que o vetor de propagação da onda está na mesma direção e é proporcional ao vetor , escreva uma possível expressão para o vetor campo elétrico em função do tempo e do espaço.
3. A partir da sua resposta do item b), escreva uma possível expressão para o vetor campo magnético em função do tempo e do espaço.

Qual das expressões abaixo pode corresponder ao campo magnético de uma onda eletromagnética polarizada na direção e que se propaga na direção e sentido de ?

(a)

(b)

(c)

(d)

(e)

(f)

Películas de Fluoreto de Magnésio () são empregadas para diminuir a quantidade de luz refletida em lentes e materiais, no espectro visível. O índice de refração desse material vale, aproximadamente, . Se a amplitude do campo elétrico de uma onda eletromagnética que está no interior de vale , estime a amplitude do campo magnético dessa onda.

a) .

b) .

c) .

d) .

3. Ondas eletromagnéticas podem ser classificadas como ondas longitudinais.

Escolha uma opção:

( ) Verdadeiro

( ) Falso

O campo elétrico de uma onda eletromagnética plana monocromática que se propaga no vácuo é dado por , onde e são constantes.

(a) (0,5 ponto) Determine a direção e o sentido de propagação da onda. Calcule o comprimento de onda e a frequência desta onda em função das constantes e .

(b) (0,5 ponto) Que relação deve haver entre e para que o campo satisfaça a equação de ondas eletromagnéticas no vácuo?

(c) (0,5 ponto) Expresse o campo magnético em função de , , e da velocidade da luz no vácuo .

(d) (1,0 ponto) Calcule o vetor de Poynting instantâneo e a densidade de energia média desta onda.

Considere uma onda eletromagnética plana e monocromática polarizada linearmente na direção que se propaga ao longo do eixo positivo de um sistema de coordenadas. O campo elétrico dessa onda pode ser escrito como:

Uma “cavidade linear” no vácuo é definida por duas paredes planas, paralelas e de material condutor ideal situadas em planos paralelos a e posicionados em e , respectivamente. Sabendo que uma onda eletromagnética é excitada dentro da cavidade no primeiro modo normal de oscilação, o campo elétrico dessa onda pode ser dado por:

a) .

b) .

c) .

d) .

As micro-ondas são exemplos de ondas eletromagnéticas com frequência na faixa de a . Suponha que um tipo de micro-onda tenha frequência igual a . Determine o seu comprimento de onda em centímetros. Considere a velocidade de propagação das ondas igual a .

Dado:

Sabendo que em uma onda eletromagnética a sua componente magnética é descrita pela equação abaixo:

Qual é o valor da amplitude da componente elétrica desta onda eletromagnética? Adote

Uma onda eletromagnética plana e monocromática possui campo magnético , vetor número de onda e frequência angular . O campo elétrico dessa onda vale?

A figura abaixo representa os campos elétrico e magnético de uma onda eletromagnética plana monocromática, no vácuo, na origem do sistema de coordenadas em dois instantes diferentes. Nestes dois momentos . A frequência da onda é e sua velocidade de propagação .

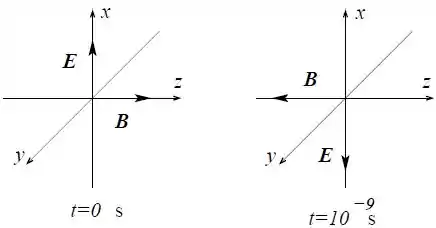
1. Determine o sentido de propagação da onda. Calcule o comprimento de onda , a frequência angular e o número de onda .
2. Escreva a expressão completa do vetor campo elétrico indicando a dependência nas coordenadas e no tempo.
3. Escreva a expressão do vetor campo magnético associado ao campo elétrico dado.

O campo magnético de uma onda propagante é dado por . A direção de polarização dessa onda é:

Um material não magnético possui a permeabilidade magnética igual à do vácuo . Um feixe de luz se propaga nesse material com velocidade . Determine o valor da permissividade elétrica desse material.

a) .

b) .

c) .

d) .

Considere uma onda eletromagnética plana, monocromática e linearmente polarizada cujo campo magnético é dado pela expressão:

Em função dos dados do enunciado, calcule o que se pede. Substitua os valores de todas as constantes fundamentais na resposta final de cada item.

(a) Determine o comprimento de onda, o período de oscilação, a direção e o sentido de propagação da onda eletromagnética.

(b) Determine o módulo da velocidade de propagação da onda.

(c) Determine o vetor campo elétrico (módulo, direção e sentido) dessa onda eletromagnética.

A figura abaixo representa os campos elétrico e magnético de uma onda eletromagnética plana monocromática, no vácuo, na origem do sistema de coordenadas em dois instantes diferentes. Nestes dois momentos . A frequência da onda é e sua velocidade de propagação .

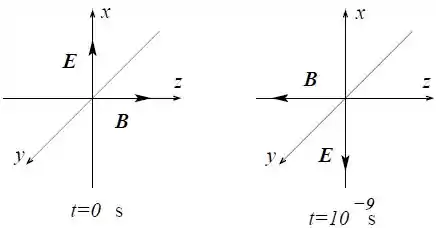
Determine o sentido de propagação da onda. Calcule o comprimento de onda , a frequência angular e o número de onda .

Escreva a expressão completa do vetor campo elétrico indicando a dependência nas coordenadas e no tempo.

Escreva a expressão do campo magnético associado ao campo elétrico dado.

Dentre os pares de campos elétrico e magnético abaixo, descritos em notação complexa (ou fasorial), qual alternativa pode representar uma onda plana eletromagnética propagando-se no vácuo?

Considere , e constantes e .

1. ,
2. ,
3. ,
4. ,
5. ,
6. ,