Velocidade e Potência de uma Onda na Corda
Teoria
Velocidade de uma onda na corda
Anteriormente, vimos que a velocidade de uma onda está relacionada ao comprimento de onda e à frequência através de:
Entretanto, podemos dizer que ela é determinada também pelas propriedades do meio!
No caso da corda...
Quando se trata da velocidade de uma onda na corda, podemos calculá-la a partir da tensão no fio e da densidade linear da corda.
Uma figura clássica que ilustra isso é essa aqui:
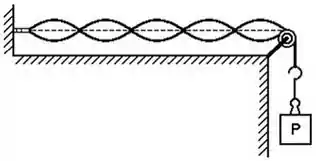
Se a massa do bloco é 5kg e a densidade linear da corda é , qual será essa velocidade na corda?
A equação que relaciona a força , tração exercida no fio, a densidade linear da corda e a velocidade da onda na corda é a seguinte:
Onde é a densidade linear de massa, que se for constante é .
Onde a tração na corda é o próprio peso do bloco que está em repouso:
Substituindo temos:
É isso que você tem que saber! Uma fórmula mágica que resolve todos os exercícios.
Esse fenômeno que a gente viu acontece no violão, quando afinamos as cordas a tração se modifica mudando por consequência a velocidade e alterando o som emitido.
Potência média de uma onda
Quando produzimos uma onda em uma corda esticada, fornecemos energia para que a corda se mova (lembre-se: todo mundo precisa de energia para se mover).
Conforme a onda vai se movendo na corda e se afastando de nós, vimos que ela vai transportando energia tanto na forma de energia cinética quanto na de potencial elástica.
Agora vamos ver como calcular a taxa média com a qual essa energia é transmitida.
A taxa média de energia transmitida não é nada mais do que a potência média da onda.
Como quantificamos isso?
Vamos calcular a potência média pro nosso exemplo da corda se aquele movimento tem uma frequência de e uma amplitude .
A potência média é dada por:
Onde:
é a velocidade da onda.
é a densidade linear da corda. Lembra disso? A densidade linear de massa é
é a amplitude.
é a frequência.
Essa fórmula assusta né? Mas tem um jeito bom de gravar!
“Me vê dois ‘piaf’ quadrados” – seja lá o que isso quer dizer. =)
Se você se lembrar dessa frase, vai lembrar que:
Também podemos chamar a potência média de intensidade, ou seja:
Observação 1: colocando as unidades de , , e no SI, a unidade de potência é (watt).
Não sei se você se ligou mas temos todos os nossos valores no então é só a gente substituir os nossos valores na equação e calcular a intensidade, se liga:
Observação 2: Você também pode encontrar a expressão acima nessa forma aqui:
Pra chegar nela é só lembrar que
Observação 3: Outra equação que pode aparecer é a potência instantânea mais roots que é a origem da nossa potência aqui em cima!
Onde é a força sobre a corda (geralmente a tensão) e é a função da onda! Essa fórmula não é muito cobrada, mas a gente não pode dar bobeira não, hein! ;)
E o que seria a densidade de energia por comprimento?
Bom, a gente pode chegar nessa expressão bem facilmente. Só você pensar que a densidade de energia por comprimento é algo do tipo:
E que a potência por definição é:
E aí é só jogar na outra equação:
E o termo nada mais é que o inverso da velocidade então reescrevendo a equação temos:
Beleza? Essa é a chamada densidade média de energia total da corda.
Substituindo a potência que calculamos e a velocidade que já tínhamos, a equação vai ficar:
Também podemos encontrar a expressão da densidade média diretamente, substituindo a potência média:
Ok, estamos prontos pra enfrentar os exercícios agora! =)
Potência média de uma onda
Exercícios Resolvidos
Exercício Resolvido #1
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 16, pp 142-15
Qual é a velocidade de uma onda transversal em uma corda de de comprimento e g de massa sujeita a uma tensão de
Passo 1
Vamos usar aqui a equação da velocidade transversal em um corda em função da densidade linear e da tensão:
Passo 2
Mas antes, precisamos do valor da densidade linear .
Então,
Resposta
Exercício Resolvido #2
USP, Física 2, Prova 1, 2014.1 – Questão 2
A tensão num fio preso em ambos os extremos é duplicada sem que haja qualquer mudança considerável em seu comprimento. Qual é a razão entre as velocidades das ondas transversais nesse fio, antes e depois do aumento de tensão?
Passo 1
Galera, aqui vamos usar a equação da velocidade transversal em uma corda em função da densidade linear e da tensão:
A velocidade antes da duplicação da tensão era:
E a nova velocidade será em função da nova tensão, :
Logo a razão entre a velocidade antes e depois fica:
Resposta
Letra: a)
Exercício Resolvido #3
UERJ, Lista P1, Lista de Ondas, Questão 2
A densidade linear de uma corda é . Uma onda transversal na corda é descrita pela equação:
Na qual e são expressos em metros e em segundos. Determine:
A velocidade de propagação da onda.
A tensão na corda.
Passo 1
Bom, galera, nesse tipo de questão o bizu é comparar a equação da onda dada com uma equação genérica das ondas.
Lembrando que essa equação genérica pode ser escrita por:
Ou, usando seno:
A conversão de uma para outra se dá ajustando a fase. Não se assuste com esse fato, lembre-se que a função cosseno é uma translação da função seno!
Passo 2
Bom, a equação da velocidade de uma onda em função do comprimento de onda e da frequência é:
Assim, se conseguirmos essas duas informações, conseguiremos calcular a velocidade!
Vamos fazer aquela comparação de equações agora:
Com:
Comparando, percebemos que:
Pronto! Substituindo na equação da velocidade:
Passo 3
Sabendo o valor da velocidade que a gente achou em , fica fácil resolver essa! A gente só precisa lembrar dessa equação:
Nós queremos saber a tensão da corda, logo:
O enunciado nos diz que , e sabemos que , então:
Pronto! (:
Resposta
Respostas:
Exercício Resolvido #4
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 16, pp 143-25
Uma corda uniforme de massa e comprimento está pendurada em um teto.
Mostre que a velocidade de uma onda transversal na corda é função de, a distância da extremidade inferior, e é dada por
Passo 1
Na primeira situação temos a seguinte figura:
Pela condição de equilíbrio, a tensão na corda vale .
E a densidade linear vale .
Aplicando a fórmula:
Como queríamos demonstrar! :)
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 16, pp 143-26
Uma corda na qual ondas podem se propagar tem m de comprimento e de massa. A tensão da corda é N. Qual deve ser a frequência de ondas progressivas com uma amplitude de mm para que a potência média seja ?
Passo 1
Como o problema fala de potência média, podemos aplicar a fórmula:
onde:
é a velocidade da onda
é a densidade linear da corda
é a amplitude
é a frequência
Não se esqueça!
Me vê dois ‘piaf’ quadrados
Pelo dados do problema, temos:
Falta !
Passo 2
Para descobrirmos , aplicamos a fórmula:
Passo 3
Agora a única incógnita é a frequência .
Substituindo os valores, chegamos a:
Resposta
Exercício Resolvido #6
PUC, Física 2, Prova 2, 2012.1 – Questão 1 - Modificada
Uma onda transversal senoidal se propaga em uma corda no sentido negativo do eixo . A Figura abaixo mostra o deslocamento em função da posição no instante . A tensão na corda é e a massa específica linear . Assuma que a onda é da forma .
Determine a amplitude.
Encontre a velocidade da onda e a frequência da onda.
Calcule a taxa média de transporte de energia.
Passo 1
Analisando o gráfico, podemos ver que a distância do eixo até um ponto de máximo, ou seja, a amplitude é:
Passo 2
Para determinar a velocidade, podemos usar a seguinte relação:
Substituindo os valores, temos:
Perceba que tivemos que passar a densidade linear para o S.I!
Para calcular a frequência, podemos usar a seguinte relação:
Do gráfico, . Então:
Novamente tivemos que passar para o S.I! Fique esperto!
Passo 3
A potencia média, taxa média de transporte de energia, é dada por:
Onde é a amplitude, substituindo os valores, temos:
Resposta
.
;
Exercício Resolvido #7
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 16, pp 143-26
Energia é transmitida a uma taxa por uma onda de frequência em uma corda sob tensão . Qual é a nova taxa de transmissão de energia em termos de
- Se a tensão é aumentada para ?
- Se, em vez disso, a frequência é reduzida para ?
Passo 1
A taxa de energia transmitida é justamente a potência média.
Então vamos aplicar a fórmula:
Como:
Chegamos a:
Passo 2
Então se quadriplicamos a tensão:
Ou seja, .
Passo 3
Com a frequência, vamos fazer a mesma coisa:
Como :
Vemos então que: