Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Momento Linear Relativístico

Ver Todos os Exercícios

Teoria

Introdução

Você que chegou até aqui deve saber bem como calcular um momento linear certo? Bom e se eu te pedir pra me ajudar a calcular o momento linear de uma partícula de 1 μ g que viaja com uma velocidade v = 0,8 c , será que a gente consegue?

O momento linear que a gente conhece é:

p → = m v →

Onde v é a velocidade da partícula, ou objeto, do qual estamos calculando o momento linear e m é a massa do objeto.

AH então é só substituir os valores aqui e já era né?

c = 3 × 10 8 m / s  

m = 10 - 6 g = 10 - 9 k g

p = 10 - 9 × 0,8 × 3 × 10 8 = 0 , 24 k g m / s

Errado! Esquecemos de considerar os efeitos da relatividade.

Momento Linear Relativístico

Mas então no caso relativístico, quais mudanças teremos?

No capítulo anterior vimos a definição de massa relativística, e vimos que quando as velocidades são muito altas a massa também sofre distorção.

Então podemos escrever a expressão do momento linear relativístico da seguinte forma:

p → = m r v →

Onde m r é a massa relativística, dada por:

m r = γ m

Lembrando que γ é o fator de Lorentz, dado por:

γ = 1 1 - v 2 / c 2

Sendo assim temos:

m r = m 1 - v 2 / c 2

M a s s a   r e l a t i v í s t i c a

Então podemos dizer que o momento linear relativístico nada mais é que:

p → = γ m v →

M o m e n t o   l i n e a r   r e l a t i v í s t i c o

Se liga! Repara que a única diferença dessa fórmula para a fórmula de momento linear que usávamos antes é o fator de Lorentz γ , que aparece multiplicando ali. A gente pode dizer que o fator de Lorentz é uma espécie de fator de correção.

Então pro nosso exemplo o primeiro passo é calcular o fator de Lorentz:

γ = 1 1 - 0,8 c c 2 = 1 0,36

γ = 10 6 = 5 3

E então como eu disse a única coisa que muda é o fator de Lorentz, vamos pegar o valor que encontramos e multiplicar por ele, beleza?

Como:

m v → = 0,24 k g m / s

p → = γ m v →

p → = 5 3 × 0,24 = 0,40 k g m / s

Viu, são bem diferentes os valores, então fique atento pra não errar isso. Se a gente analisar graficamente a relação dos momentos lineares poderemos ver o quão diferente são conforme a velocidade se aproxima á da luz.

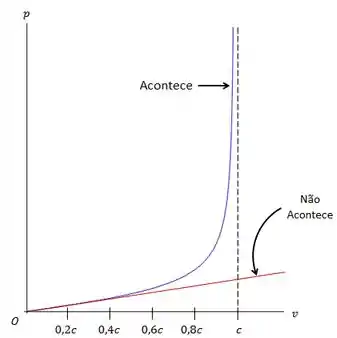
A linha vermelha representa a expressão do momento linear que usávamos até então p → = m v → e a linha azul representa a expressão do momento linear relativístico.

Correlações importantes!

Existem outras relações entre energia relativística e momento relativístico que são muito importantes!

Lembra que a energia total relativística era dada por:

E = γ m c 2

A primeira delas nós encontramos quando multiplicamos o momento relativístico por c 2 e comparamos com a energia. Dá uma olhada!

p c 2 = γ m v c 2 = E v

Se a gente rearrumar então temos:

v c = p c E

Esta é a primeira relação!

A segunda é uma equação que relaciona a energia total E , a energia em repouso m c 2 e o momento linear p , e a gente costuma dizer que esse é o “Teorema de Pitágoras relativístico”.

Existe uma forma matemática que leva um pouco de tempo pra chegar nessa equação. Porém após deduzida, a galera percebeu uma forma mais fácil de calculá-la, é só montar o seguinte triângulo:

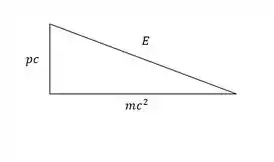
E aplicar nele o teorema de Pitágoras:

E 2 = m c 2 2 + p c 2

Ou:

γ m c 2 2 = m c 2 2 + p c 2

Também podemos relacionar o momento linear com a energia cinética relativística:

E = E C + E R e p o u s o

Onde:

E r e p o u s o = m c 2

E - m c 2 = E C

E substituindo o valor da energia total temos:

γ m c 2 - m c 2 = E C

E c = m c 2 γ - 1

E pra achar a relação é só multiplicar os dois lados por v :

E c v = p c 2 γ - 1

Vamos aplicar isso?

Um elétron possui energia cinética de 2,53 M e V , sabendo que a energia em repouso do elétron é m c 2 = 0,511 M e V calcule o momento linear em função da velocidade da luz:

Vamos começar usando a equação da energia total:

E = E c + E R e p

E = 2,53 + 0,511 = 3,041 M e V

Agora usando o teorema de Pitágoras relativístico temos:

E 2 = m c 2 2 + p c 2

p 2 c 2 = E 2 - m c 2 2

Extraindo a raiz:

p c = ( E 2 - m c 2 2 )

Agora vamos substituir os valores conhecidos:

p c = 3,041 2 - 0,511 2

p c = 2,99 M e V . m / s

p = 2,99 c M e V

É comum os exercícios cobrarem o momento linear em função da velocidade da luz c , e até nas provas fica mais fácil de corrigir.

O foco principal é saber usar as relações e não esquecer do fator de Lorentz pra esse tipo de momento linear, beleza?

Bora pros exercícios!

Correlações importantes!

Exercícios Resolvidos

Exercício Resolvido #1

David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, Volume 4 , 8º ed. Rio de Janeiro: LTC , 2008, pp 180-45.

Qual deve ser o momento de uma partícula de massa m para que a energia total da partícula seja 3,0 vezes maior que a energia de repouso?

Passo 1

A equação que relaciona a energia total, o momento linear e a energia de repouso é dada por:

E 2 = m c 2 2 + p c 2

E com ela mesmo vamos conseguir resolver a nossa vida. Já que queremos saber o momento para o qual E = 3 m c 2 , vamos jogar isso na equação de cima e organizar os termos aos poucos, beleza?

3 m c 2 2 = m c 2 2 + p c 2

Show! Vamos arrumar isso:

9 m c 2 2 = m c 2 2 + p c 2

9 m c 2 2 - m c 2 2 = p c 2

8 m c 2 2 = p c 2

p c = 8 m c 2

Finalmente:

p = 8 m c

p ≅ 2,83 m c

Resposta

p ≅ 2,83 m c

Exercício Resolvido #2

PUCRIO-P3-2013.1-1c

A energia total de um elétron em uma certa fissão nuclear é 2,40   M e V .

c ) Calcule o momento linear p e em M e V / c e a velocidade u desse elétron em função de c . A energia de repouso do elétron é 0,511   M e V .

Passo 1

Quando temos o valor da energia total dado, temos sempre que lembrar da fórmula da energia total. Vamos primeiro determinar o momento linear. Para isso, vamos utilizar a fórmula de energia total:

E 2 = p . c 2 + m . c 2 2

Onde ( m . c 2 ) , como sabemos, é a energia de repouso, que também foi dada. Então, para achar o momento linear, é só substituir:

2,40 2 = p . c 2 + 0,511 2

Como está tudo em M e V , não precisamos nos preocupar em substituir as unidades!

p . c = 5,499

p = 2,345   M e V / c

Passo 2

Agora que temos o momento linear, podemos determinar a velocidade, é só lembrar da relação entre os dois valores:

p = E c 2 . u

Substituindo os valores, temos:

Ahhh...não se esqueça que o momento linear está dividido por c . E como está tudo na mesma unidade, não precisamos nos preocupar!

2,345 c = 2,40 c 2 . u

u = 0.977 . c

Resposta

c ) p = 2,345   M e V / c ; u = 0.977 . c

Exercício Resolvido #3

PUCRIO-P3-2013.2-1b

O momento linear de um próton é 2,5   G e V / c .

Calcule a energia total desse próton em G e V .

Passo 1

Para determinar a energia total através do momento linear, podemos utilizar a seguinte relação:

E 2 = p . c 2 + m . c 2 2

Sabendo que:

m p . c 2 = 0,93957   G e V

Calma....esses valores normalmente são dados na capa da prova!

Passo 2

Teremos para a energia do próton:

E p 2 = p . c 2 + m p . c 2 2

Substituindo os valores, fica:

E p 2 = 2,5 2 + 0,938 2

Opaaa...onde foi parar o c que estava multiplicando o momento linear? Calma...o momento foi dado em G e V / c , e por isso é só cortar o c ! Ahh...como está tudo em G e V , não precisamos nos preocupar em igualar as unidades. Mas fique sempre de olho nisso!

Passo 3

Voltando para a energia total, temos:

E p = 7,13

E p = 2,67   G e V

Resposta

E p = 2,67   G e V

Exercícios de Livros Relacionados

28. Quando você deve usar a relatividade? Como você viu, os cálculos relativísticos costumam envolver a grandeza γ . Quando γ é significativamente maior do que um, devemos usar fórmulas relativísticas
29. a ) Para qual valor da velocidade o momento linear de uma partícula é igual ao dobro do valor da expressão não-relativística m v ? Expresse sua resposta em termos da velocidade da luz. b ) Uma for
A partícula K0 tem uma massa de 497,7 MeV / c2. Ele decai em π– e π +, cada um com massa de 139,6 MeV / c2. Após a decadência de um K0, um dos píons está em repouso no laboratório. Determine a energia
Mostre que a velocidade de um corpo com momento de módulo p e massa m é u = c 1 + m c p 2
O limite de velocidade em certa rodovia é de 90,0k m / h . Suponha que as multas de velocidade sejam dadas proporcionalmente à quantidade pela qual o momento do veículo excede o momento que teria se e