Colisão Elástica
Produzido por Ludovic BeghinTeoria
Fala aí! Seja muito bem vindo ao Responde Aí! Bora conversar sobre Colisão Elástica?
O que é uma Colisão Elástica?
Sempre que tivermos uma colisão elástica vai haver a conservação do momento linear e da energia cinética após o choque entre dois corpos!
Como Identificar Colisões Elásticas?
Pra entendermos melhor como identificar colisões elásticas, vamos olhar esse caso super clássico:
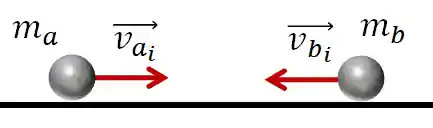
Temos duas bolinhas, uma indo em direção da outra. Elas vão se chocar e depois cada uma vai seguir seu caminho com velocidades diferentes das iniciais.
Podemos descrever a colisão elástica usando duas expressões, uma para conservação do momento linear e outra para a conservação da energia cinética!
📢 Clique para ver mais:
- Colisão Elástica: Exercícios Resolvidos
- Colisão Inelástica
- Sistemas de Partículas: Aulão Salva Vidas
Quer aprender mais?! Nesse vídeozinho a gente fala mais sobre como identificar uma colisão elástica e como resolver problemas! 👇
Conservação do Momento Linear
Na colisão elástica, temos então o momento linear inicial igual a final:
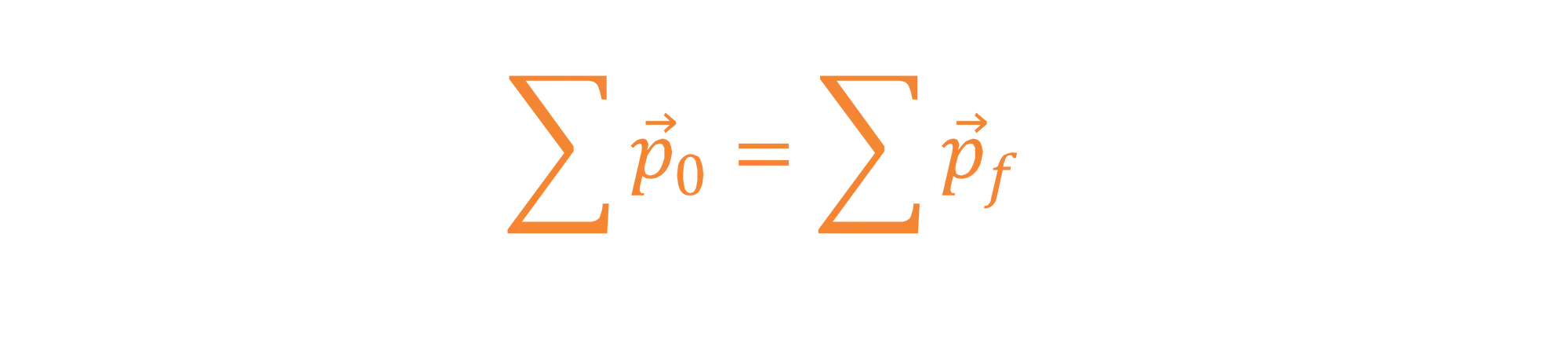
Abrindo essa expressão para o nosso exemplo, ficamos com:
A massa das bolinhas vão se manter, mas as velocidades vão mudar! Do lado esquerdo, temos o Momento Linear Inicial do sistema e do lado direito o Momento Linear Final do sistema.
Conservação da Energia Cinética
Agora, a conservação da energia cinética escrevemos como:
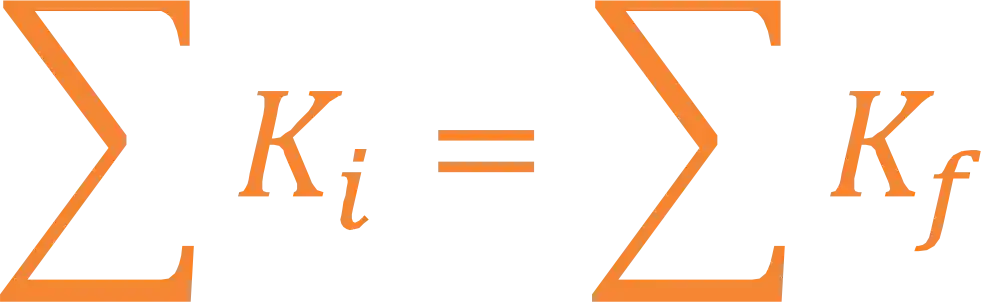
Abrindo a expressão:
A mesma coisa aqui, do lado esquerdo, temos o Energia Cinética Inicial do sistema e do lado direito o Energia Cinética Final do sistema.
Exemplo: Como Calcular a Velocidades após uma Colisão Elástica
Pra tudo ficar mais claro, vamos fazer um exemplo juntinhos!
Vamos supor uma bolinha 1 de massa
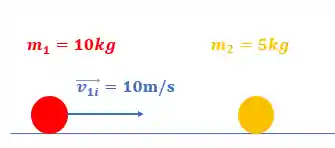
Depois que ocorrer a colisão, as duas bolinhas terão velocidades finais diferentes das iniciais que desejamos saber:
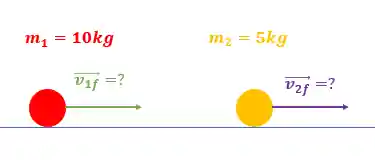
Passo 1: Conservação do Momento Linear
Vamos começar pela equação da Conservação do Momento Linear:
Substituindo os valores:
Agora damos uma arrumadinha, e como estamos na mesma direção, podemos tirar as setinhas:
Passo 2: Conservação da Energia Cinética
Agora chegou a vez da conservação da energia cinética:
Substituindo os valores:
Organizando:
Passo 3: Calcular as velocidades finais
Até agora chegamos em:
Agora chegou a hora de substituir! Substituindo
Fazendo esse produto notável:
Logo temos uma equação do segundo grau:
Resolvendo a equação de segundo grau, chegamos em:
Como sabemos que a bolinha 1 colidiu com outra bolinha, logo sua velocidade não pode continuar a mesma! Logo:
Aweee! Agora, bora praticar com mais exercícios?
Exemplo: Como Calcular a Velocidades após uma Colisão Elástica
Exercícios Resolvidos
Exercício Resolvido #1
UERJ – 2ª Lista
Considere um choque frontal entre duas bolinhas, como esquematizado na figura abaixo (; ; ; ):

Supondo que a colisão seja elástica (a energia mecânica se conserva), calcule as velocidades após o choque.
Passo 1
Para determinar a velocidade das bolinhas após a colisão, vamos utilizar do dado que a colisão é elástica logo conserva energia mecânica.
Antes da colisão temos somente as bolinhas se movimentando, portanto só temos energia cinética, temos então:
Substituindo os valores, temos:
Depois da colisão, também teremos somente energia cinética, temos então:
Onde e são as velocidades depois da colisão das bolinhas e respectivamente.
Substituindo os valores, temos:
Igualando a energia antes com a energia depois, temos:
Vishh, temos duas variáveis e e só uma equação, por isso, temos que utilizar outro artifício, devemos lembrar que em uma colisão em um sistema isolado (sem ação de outras forças), temos que o momento linear sempre se conserva! Vamos então utilizar a conservação do momento linear!
Passo 2
De acordo com a conservação do momento linear, temos:
substituindo os valores, temos:
Pronto!! Agora temos duas equações e duas incógnitas. A primeira equação vem do “passo ”, onde fizemos a conservação da energia mecânica e a segunda equação vem da conservação do momento linear:
Agora é só resolver esse sistema!
Substituindo o valor de na primeira equação, temos:
Resolvendo essa equação do segundo grau, encontramos duas raízes, no entanto, temos que a única raiz possível é:
(a outra raiz é , que é a velocidade antes da colisão, por isso não é uma solução possível já que sabemos que a velocidade tem que mudar!)
Dessa forma, a velocidade da bolinha depois da colisão é:
Resposta
Exercício Resolvido #2
USP – 2ª Prova – 2014
Dois pêndulos de comprimento estão suspensos juntos conforme a figura abaixo. O pêndulo (de massa ) é solto a partir do repouso de uma altura enquanto que o pêndulo (de massa ) está em repouso na posição vertical.
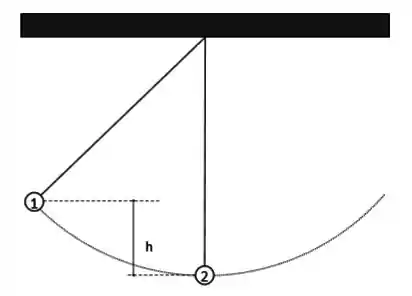
Considerando inicialmente que a colisão é elástica determine:
A velocidade do pêndulo imediatamente antes do choque.
A velocidade de cada pêndulo imediatamente depois do choque.
Dado: .
Passo 1
Por conservação de energia:
Tomando o ponto mais baixo como referencial de energia potencial nula, e lembrando que o pendulo parte do repouso, portanto :
Passo 2
Visto que o enunciado informou para tratarmos como uma colisão elástica, ou seja, sem perdas de energia. Podemos utilizar conservação de energia cinética e conservação de momento linear.
Por conservação de momento linear:
O Pendulo estava em repouso antes da colisão, portanto .
Por conservação de energia cinética:
Novamente, lembremos que
Ficamos então com o sistema:
Substituindo a primeira equação na segunda temos:
Substituindo agora o na primeira equação do sistema:
Substituindo agora que , e .
Lembrando que:
Resposta
Exercício Resolvido #3
UFRJ – 2ª Prova – 2015.1a
Um bloco de massa está em equilíbrio preso a uma mola ideal, de constante elástica , inicialmente em sua posição relaxada, como mostra a figura. Uma bala de massa com velocidade horizontal de módulo colide com esse bloco de modo que a bala retorna após a colisão no sentido oposto com velocidade de módulo .
Considere que: a colisão é instantânea; que a mola é ideal; que a resistência do ar é desprezível; e que a gravidade tem módulo conhecido.
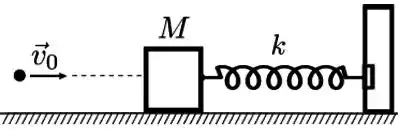
Determine, em função dos dados do problema:
A razão para que a colisão seja elástica.
Passo 1
Para a colisão ser elástica, a energia cinética deve se conservar!
Antes da colisão, o bloco está parado, então a energia cinética total do sistema bala+bloco é a energia cinética da bala
Depois da colisão, a velocidade da bala é e a do bloco é . Então a energia cinética final do sistema é
Logo, a equação de conservação da energia cinética é:
Passo 2
Bom, temos as massas as quais queremos saber a razão entre elas, mas ainda temos a velocidade do bloco como incógnita, então temos que descobri-la e faremos isso por conservação de momento linear.
Como estamos estudando uma colisão, e o enunciado ainda fez questão de enfatizar ser instantânea, vamos usar a relação que na colisão há conservação de momento linear, então
Vamos analisar o momento linear antes do impacto:
A bala tem massa e velocidade inicial de módulo , enquanto o bloco tem massa , mas está parado.
Vamos definir o sentido de (pra direita) como positivo. Então o momento linear total do sistema bala+bloco logo antes da colisão, em módulo, é:
Passo 3
Agora o momento linear depois da colisão:
Logo após a colisão, a bala volta com velocidade de módulo no sentido oposto, então sua velocidade agora é negativa. E o bloco vai ter a velocidade , que é justamente o que a gente quer achar!
Então o módulo do momento linear total do sistema logo após a colisão é:
Voltando pra equação da conservação do momento linear:
Passo 4
Agora que temos , podemos resolver a equação que achamos pela conservação de energia, basta multiplicar tudo por 2 e substituir :
Podemos dividir tudo por , aí sobra:
Então pra colisão ser elástica, devemos ter
Resposta
Exercício Resolvido #4
UERJ – 2ª Lista
Uma bolinha de massa e velocidade colide com outra bolinha de massa (inicialmente em repouso) como mostra a figura abaixo. Considere que o choque é elástico (a energia mecânica se conserva) e que .
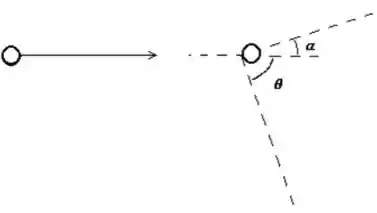
Escreva as equações de conservação de e de .
Calcule as velocidades finais.
Passo 1
Quando temos uma colisão elástica, temos que a energia mecânica total do sistema se conserva. No caso do nosso sistema, onde temos duas bolinhas, a equação da conservação da energia mecânica será:
Sabendo que as massas são iguais, e que , temos:
Passo 2
Pela figura, podemos perceber que se trata de uma colisão em duas dimensões, quando isso ocorre, podemos tratar cada coordenada separadamente. Para o momento linear, ou quantidade de movimento, temos:
No eixo :
sabendo que as massas são iguais, e , temos:
No eixo :
sabendo que as massas são iguais, e que , temos:
Agora que temos todas as equações, vamos para a letra !
Passo 3
Para determinar a velocidade final das bolinhas temos que lembrar da relação entre o módulo das velocidades e suas componentes, pela regra do “COlado/SEparado”
sabendo da relação , temos:
Agora que temos as componentes da velocidade final da bolinha em função do módulo da velocidade, podemos agora achar a mesma relação só que para a bolinha !
Passo 4
Pela conservação do momento linear no eixo , temos:
ou seja:
Pela conservação do momento linear no eixo , temos:
Substituindo , temos:
Agora que temos todas as componentes em função do módulo da velocidade final da bolinha , é só substituir na equação da conservação da energia mecânica, se liga no próximo passo!
Passo 5
Pela equação da conservação da energia mecânica, temos:
substituindo os valores em função de :
Substituindo na equação na energia mecânica, podemos determinar a velocidade da bolinha !
Resposta
Conservação da Energia Mecânica:
Conservação do Momento Linear:
;
Exercício Resolvido #5
PUC-RIO – 2ª Prova – 2013.1
Uma bola de massa , com velocidade de que faz um ângulo de com a horizontal, atinge o centro de uma placa, também de massa , que se encontra inicialmente em repouso. Durante a colisão não há atrito e, devido à colisão, podemos considerar que a placa se move apenas verticalmente. Considerando esta colisão elástica, determine:
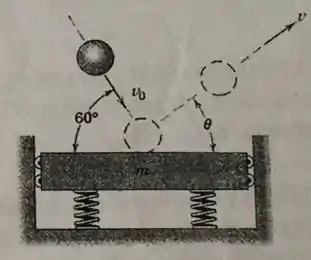
Que grandezas são conservadas nesta colisão. Justifique.
A direção e sentido dos vetores impulso atuando sobre a placa e sobre a bola.
O vetor velocidade final de ambas as massas, bola e placa, logo após o impacto.
O vetor força média que atuou na bola sabendo que o tempo da colisão foi de .
Passo 1
Em uma colisão, temos que o momento linear se conserva, pois não atuam forças externas ao sistema. Por se tratar de uma colisão elástica, temos que a energia cinética também se conserva.
Passo 2
Para determinar o vetor impulso, vamos relembrar sua definição:
No caso da placa, como não há movimento no eixo nem antes nem depois da colisão temos que o impulso é zero.
Já no eixo , pela equação de momento temos
Como o momento inicial da placa é zero, pois ela estava em repouso, descobrimos que haverá impulso na direção
Agora só precisamos descobrir o sentido desse vetor. Para isso vamos abrir a equação de momento
Onde é a velocidade da placa depois da colisão, olhando a imagem vemos que a bola vai colidir com a placa e empurrá-la para baixo, assim o único sentido possível para o movimento da placa é para baixo (sentido negativo do eixo ).
Sendo assim definimos o sentido da velocidade da placa que será negativa, implicando que o impulso em será no sentido negativo também.
Assim o vetor impulso na placa é dado por
Agora vamos estudar o caso da bola,
Como no item dissemos que o momento linear se conserva, devido a isso sabemos que o impulso resultante no sistema deve ser zero.
O nosso sistema é composto por bola e placa, terminamos de dizer a direção e sentido do impulso na placa, para que a resultante do impulso no sistema seja zero, temos que o impulso na bola é na mesma direção e módulo do impulso na placa, porém com o sentido oposto.
O impulso na bola pode ser dado por
Passo 3
Para descobrirmos a velocidade final da bola, vamos aplicar conservação de momento em cada eixo do sistema.
Começando pelo eixo , pois apenas a bola consegue se movimentar nesse eixo.
Sendo assim temos que
Cortando a massa e isolando , chegamos na primeira equação
Agora, vamos analisar o eixo , onde por conservação de momento temos
No momento antes da colisão só a bola se movimentava e depois da colisão a bola continua a se movimentar, mas a placa começa a se movimentar também, então podemos reescrever a fórmula acima
Como já vimos é negativa, e podemos cortar a massa, chegamos na nossa segunda equação
Podemos agora substituir a primeira equação na segunda e obtemos
Lembrando que seno dividido por cosseno é tangente e isolando , chegamos na nossa terceira equação
Passo 4
Precisamos de mais uma equação para resolver o problema, já usamos conservação de momento linear, então agora vamos usar o fato que a energia cinética também se conserva.
Então vamos ter
Cortando tudo que se repete nos três termos da equação chegamos na nossa quarta equação
Agora, substituindo a primeira e a terceira equação na quarta temos
Passo 5
Precisamos resolver essa equação agora, podemos cortar
Tirando o do denominador e abrindo a tangente em seno e cosseno
Lembrando da relação fundamental, onde
Assim, chegamos na equação
Temos a solução onde , e a solução onde
Assim, a outra solução é
Essa solução não serve para gente, pois iria violar uma das conservações, basta substituir nas fórmulas para conferir.
Vamos então usar a solução , assim substituindo na primeira equação temos que a velocidade da bola depois da colisão é
Agora, para achar a velocidade da placa depois da colisão é só substituir na equação
Passo 6
Para calcularmos a força média aplicada na bola, vamos usar a fórmula
No “passo 2” vimos que o impulso aplicado na bola é igual
Assim,
Substituindo o valor de , e
Resposta
e
Bola: Direção sentido positivo
Placa: Direção sentido negativo