Colisão Inelástica
Produzido por Ludovic BeghinTeoria
Quando dois objetos colidem e não há nenhuma perda de energia cinética, temos uma colisão elástica. Mas e quando nos deparamos com um exercício onde temos dissipação de energia cinética, como fazer?!
O que são Colisões Inelásticas?
Em uma colisão inelástica a energia cinética não é preservada! Ela pode ser transformada em energia térmica, sonora ou então pode haver deformação do material.
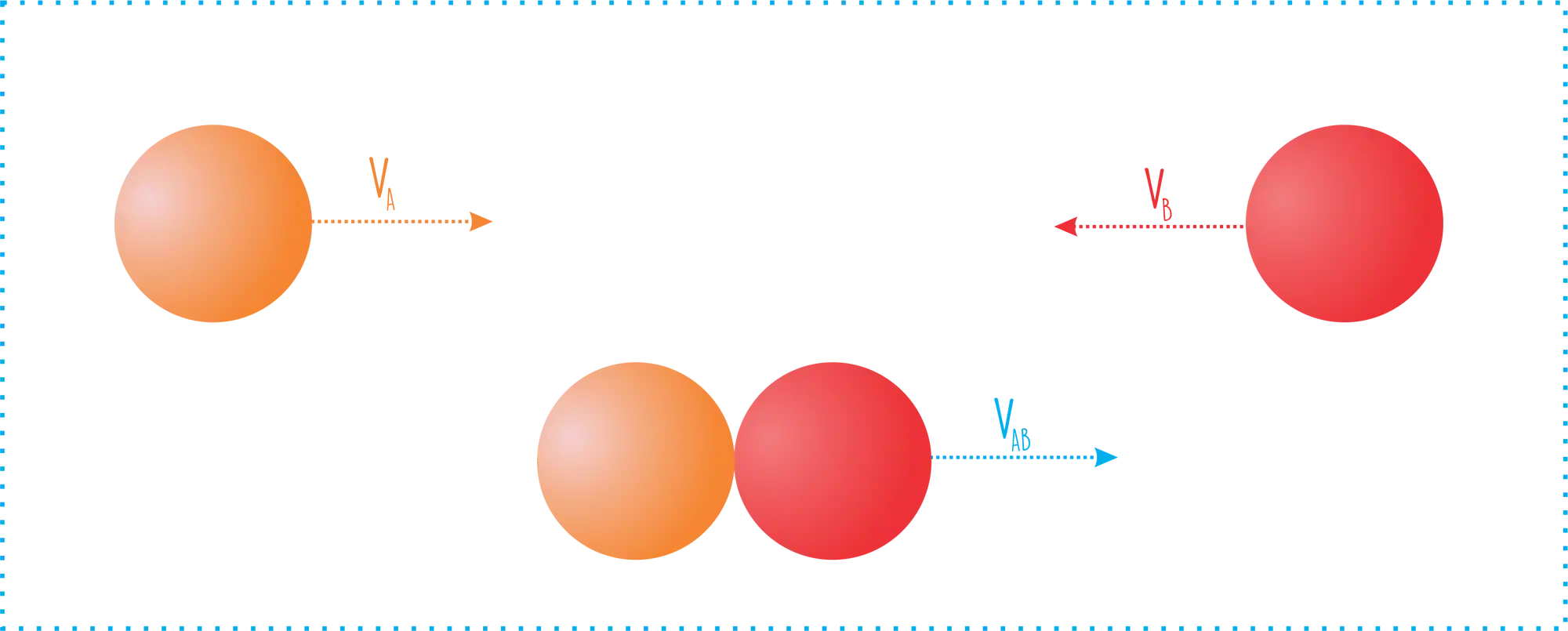
Existe, no entanto a conservação do momento linear. Então quando você se deparar com um problema que não especifica o tipo de colisão, é no momento linear que você vai se agarrar!
Podemos ter uma colisão perfeitamente inelástica ou parcialmente inelástica, mas não precisa se preocupar! Já já a gente vai aprender como diferenciar esses dois casos!
Conservação de Momento Linear
Nas colisões, teremos a conservação de momento linear
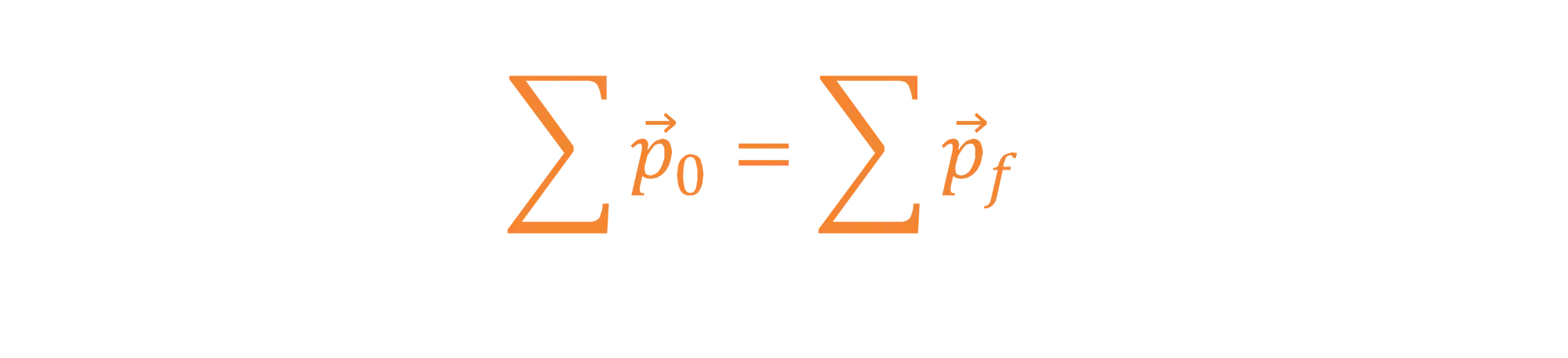
Lembrando que o momento linear é um vetor, então podemos dizer que:
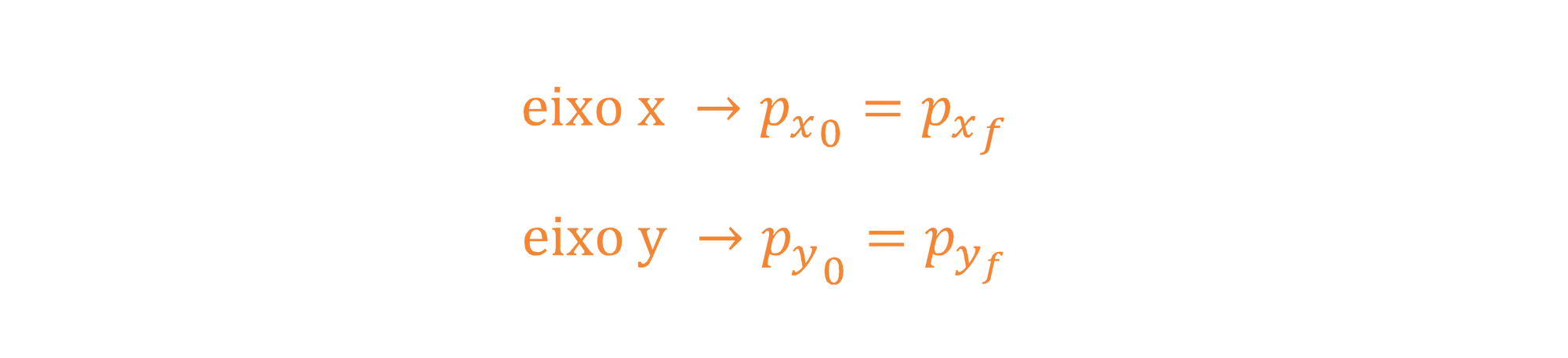
📢 Clique para ver mais:
- Colisão Inelástica: Exercícios Resolvidos
- Colisão Elástica
- Sistemas de Partículas: Aulão Salva Vidas
- Fórmula da Energia Cinética
Quer aprender mais sobre colisões inelásticas e como resolver exercícios?! Se liga nesse vídeo super completo que a gente separou pra você?! 🧡 👇
Dissipação de Energia Cinética
A principal característica de uma colisão inelástica é que há dissipação de energia cinética, ou seja, a energia cinética não se conserva, assim:
Por isso, a menos que o enunciado forneça quanto de energia foi dissipada, não poderemos usar fórmula da energia cinética para ajudar a resolver o exercício. Pelo contrário, um dos itens pedidos pelo enunciado geralmente será de calcular a variação da energia cinética!
Colisão Perfeitamente Inelástica
A colisão inelástica pode ser classificada em parcialmente inelástica ou totalmente inelástica. Colisão parcialmente inelástica é aquela em que ocorre dissipação de energia cinética, mas os objetos tem velocidade final diferente.
Vamos dar atenção a colisão totalmente inelástica, pois em uma colisão totalmente inelástica a velocidade final do objetos é a mesma, ou seja, ao final da colisão os corpos movimentam-se juntos. Assim temos que
Pela conservação de momento linear em uma colisão, podemos relacionar a velocidade final com a velocidade inicial:
Assim, a velocidade final de uma colisão totalmente inelástica é dada por:
E caso o problema seja de uma partícula com velocidade inicial
E ainda poderíamos calcular a razão entre a energia cinética final pela inicial:
Caso Especial: Explosão
Em colisões inelásticas, as explosões são colisões inelásticas acontecendo do final para o início!
Mas como assim?? !
Calma, é simples: em exercícios assim, no estado inicial as partículas movimentam-se unidas e por isso têm mesma velocidade, então ocorre a explosão e elas se separam, por isso no estado final elas estão separadas.
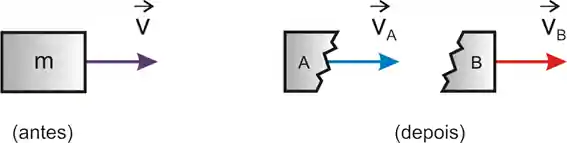
Tudo que estudamos aqui foi unidimensional, mas o raciocínio para movimentos bidimensionais é o mesmo, analise separadamente o movimento em
Agora vamos praticar com exercícios?!
Colisão Perfeitamente Inelástica
Caso Especial: Explosão
Exercícios Resolvidos
Exercício Resolvido #1
UFRJ – 2ª Prova – 2015.1
Considere um sistema isolado formado por duas partículas. Suas massas valem e e, num referencial inercial, suas velocidades são, respectivamente,
Estas partículas sofrem uma colisão totalmente inelástica. Qual o valor da energia cinética do sistema, após a colisão?
Passo 1
Temos uma colisão num sistema isolado, então o momento linear total se conserva:
Além disso, a colisão é totalmente inelástica: isso significa que as partículas saem coladas, formando uma partícula de massa e de velocidade final .
Considerando isso, a equação de conservação do momento linear é:
Passo 2
Show! Substituindo os valores do enunciado, isso fica:
Passo 3
Beleza, mas pra achar a energia cinética final, a gente precisa do módulo de .
Vamos ter:
Passo 4
Então a energia cinética final é:
Resposta
Alternativa
Exercício Resolvido #2
PUC-RIO – 2ª Prova – 2009.2
Um pêndulo balístico é um dispositivo utilizado para medir a velocidade de um projétil quando ele deixa o cano de uma arma. Esta velocidade é chamada de velocidade de saída do projétil. Um projétil de massa é disparado horizontalmente contra um bloco de madeira de massa que forma o peso de um pêndulo. O projétil penetra no bloco e o observador mede então a altura máxima atingida pelo conjunto formado pelo bloco e pelo projétil. Responda:
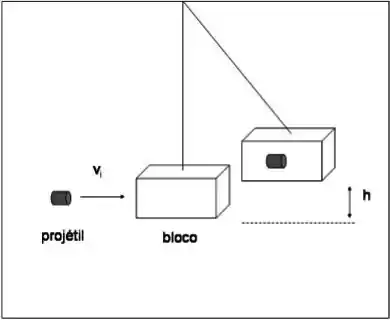
Alguma grandeza é conservada nesta colisão? Por quê?
Qual é a velocidade do sistema projétil + bloco imediatamente após a colisão sabendo que o sistema atinge a altura máxima de ?
Qual é a velocidade inicial do projétil?
Passo 1
Esta colisão é inelástica uma vez que o projétil fica preso dentro do bloco.
A única grandeza conservada é então o momento linear, pois durante o processo de colisão o somatório de todas as forças que atuam no sistema é nulo.
Passo 2
Após a colisão, e considerando que o projétil está parado dentro do bloco, podemos aplicar a conservação de energia mecânica:
Como
E
E a velocidade na altura máxima é zero, temos que
Assim,
Logo:
Substituindo os valores chegamos em
Passo 3
A velocidade inicial do projétil é dada pela conservação do momento. Então, temos que:
Consequentemente:
Substituindo o valor das massas e da velocidade final que acabamos de encontrar chegamos em:
Resposta
O momento linear, pois o somatório de todas as forças que atuam no sistema é nulo.
Exercício Resolvido #3
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp – 256
As esferas (massa ), (massa ) e (massa ) se aproximam da origem deslizando sobre uma mesa de ar sem atrito. As velocidades de e são indicadas na figura. Todas as três esferas atingem a origem ao mesmo instante e ficam coladas. Quais devem ser os componentes e da velocidade inicial de para que os três objetos unidos se desloquem a no sentido do eixo após a colisão? Se possui velocidade encontrada no item (a), qual é a variação da energia cinética do sistema das três esferas ocasionada pela colisão?
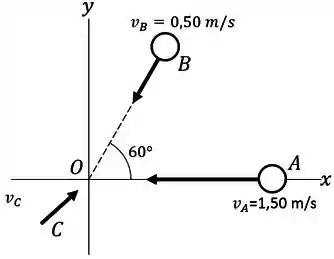
Passo 1
Temos uma colisão acontecendo, assim a primeira coisa a saber é que o momento linear do sistema é constante.
Ele não define a colisão, mas diz que as esferas ficam coladas, então depois da colisão todas tem a mesma velocidade, isso é o mesmo que falar que a colisão é inelástica.
Passo 2
Vamos escrever cada velocidade que sabemos pelo enunciado
Ambas negativas devido ao sentido do movimento, contra o eixo e . E ainda temos a velocidade final de todas
Passo 3
Para a velocidade do corpo vamos precisar decompor a velocidade usando a “regra do COlado/SEparado”
Então
Passo 4
Vamos calcular o momento linear antes e depois e usar a conservação dele.
Primeiro vamos calcular o momento linear inicial , que é dado por
Agora, vamos calcular o momento linear final
Passo 5
Igualando os momentos lineares vamos ter
Passo 6
Para achar a variação de energia cinética devemos achar a energia do sistema antes e depois.
A energia cinética antes é
Para a energia cinética devemos ter o módulo da velocidade dos corpos, precisamos então achar o módulo da velocidade de
Passo 7
Vamos ter então
Passo 8
Vamos agora achar a energia cinética do conjunto depois do choque
Passo 9
A variação de energia cinética é
Resposta
Exercício Resolvido #4
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp – 257
Uma bala de disparada por um rifle penetra e fica retida em um bloco de ligado a uma mola e apoiado sobre uma superfície horizontal sem atrito. O impacto produz uma compressão de na mola. A calibração mostra que uma força de comprime a mola . Calcule o módulo da velocidade do bloco imediatamente após o impacto. Qual era a velocidade inicial da bala?
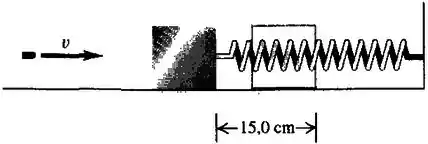
Passo 1
Temos uma colisão acontecendo, assim a primeira coisa a saber é que o momento linear do sistema é constante.
Ele não define a colisão, mas diz que as esferas ficam coladas, então depois da colisão todas tem a mesma velocidade, isso é o mesmo que falar que a colisão é inelástica.
Passo 2
Após o impacto, não vamos ter forças dissipativas, como o atrito, atuando. Isso nós diz que a energia mecânica do sistema DEPOIS da colisão é constante.
Beleza agora a energia final
A compressão da mola foi de , assim
Repara que se igualarmos não vamos resolver nada porque temos duas incógnitas.
Passo 3
O enunciado nos diz que a calibração para comprime a mola , então
Agora temos a energia mecânica final
Passo 4
Sabemos agora que
Igualando as energias
Passo 5
Vamos agora usar a conservação do momento linear, como estamos trabalhando com uma dimensão não precisamos escrever vetorialmente.
Substituindo os valores dados e a velocidade final do conjunto que acabamos de encontrar, temos
Resposta
Exercício Resolvido #5
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp. 276–17
Sobre uma mesa de ar horizontal sem atrito, o disco de hóquei (com massa igual a ) se desloca de encontro ao disco de hóquei (com massa igual a ), que inicialmente está em repouso. Depois da colisão o disco de hóquei possui velocidade igual a da direita para a esquerda e o disco de hóquei possui velocidade igual a da esquerda para a direita. Qual era a velocidade do disco de hóquei antes da colisão? Calcule a variação da energia cinética total do sistema ocorrida durante a colisão.
Passo 1
Como o problema não diz qual é o tipo de colisão, só podemos dizer que o momento linear do sistema se conserva. Sendo assim vamos usar a equação
Não precisamos usar a fórmula vetorial, pois o movimento é unidimensional
Passo 2
Para descobrir a velocidade inical do disco , basta substituir os valores dado pelo enunciado na equação acima
Positivo, o que significa que o disco inicialmente se locomovia da esquerda para a direita
Passo 3
A enercia cinética inicial é dada por
Já a energia cinética final é dada por
Passo 4
Agora podemos fazer a variação de energia cinética
Resposta
Exercício Resolvido #6
UFRJ – Prova Final – 2014.1
Duas partículas e de massas iguais colidem unidimensionalmente ao longo do eixo . Os gráficos a seguir representam as velocidades em função do tempo para cada partícula. Se é o momento linear do sistema formado pelas duas partículas e sua energia cinética, podemos afirmar que nessa colisão
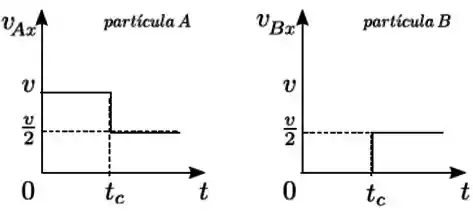
se conserva e não se conserva
se conserva e se conserva
não se conserva e não se conserva
não se conserva e se conserva
e
Passo 1
Digamos que as partículas têm massa .
Podemos ver, pelo gráfico, que antes da colisão a partícula tem velocidade positiva e de módulo , então vamos chamá-la de .
Por outro lado, a partícula está em repouso.
Então o momento linear inicial do sistema antes da colisão é:
Passo 2
E depois da colisão, as 2 partículas têm velocidade . Então o momento linear final do sistema depois da colisão é:
Portanto, o momento linear se conserva.
Passo 3
Vamos pra energia cinética!
Inicialmente, a energia cinética do sistema é
Passo 4
E depois da colisão, a energia cinética é
Logo, a energia cinética não se conserva, que é o que acontece na maioria das colisões (ela só se conserva quando a colisão é elástica) o que caracteriza uma colisão inelástica.
Resposta
Alternativa
Exercício Resolvido #7
UFRJ – 2ª Prova – 2013.1
Dois objetos de mesma massa e dimensões desprezíveis colidem no espaço sideral, na ausência de forças externas. A figura mostra um sistema de eixos de um referencial inercial, com seus unitários e . Antes da colisão os objetos se movem ao longo do eixo com velocidades de sentidos opostos, como indicados na figura, e módulos e , nos quais é uma constante dada. Após a colisão, um os objetos adquire velocidade (na figura de baixo apenas um dos objetos é mostrado).
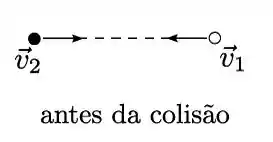
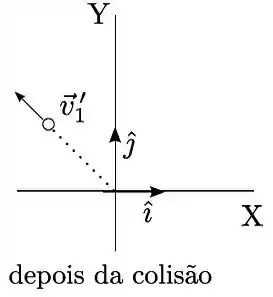
Determine a velocidade do outro objeto após a colisão, expressando sua resposta em termos da constante e dos unitários e .
Determine a razão entre a energia cinética do par de objetos depois da colisão e sua energia cinética antes da colisão; esta colisão é elástica ou inelástica?
Passo 1
Como não temos ação de forças externas o momento linear se conserva.
Vamos calcular o momento liner antes da colisão
Onde
E
Resultando em
Passo 2
Agora vamos calcular o momento linear depois da colisão
Onde
E
Resultando em
Passo 3
Como os momentos lineares se conservam
Passo 4
Vamos ter nas energias cinéticas as seguintes contas, começando pela energia cinética antes da colisão
Passo 5
Agora para a energia cinética após a colisão
Repara que vamos usar o módulo da velocidade na energia cinética, sabemos que
Vamos achar agora
Não precisamos fazer a raiz já que na fórmula está ao quadrado
Passo 6
Vamos ter a seguinte razão para
Como a energia cinética não é igual ele é uma colisão inelástica, no caso parcialmente elástica.
Resposta
a)
b)
c) colisão inelástica, no caso parcialmente elástica.
Exercício Resolvido #8
UFF – 2ª Prova – 2014.2
A figura mostra o resultado de uma colisão entre dois corpos de massas desiguais. Determine:
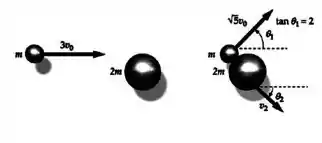
O ângulo
A rapidez da maior massa após a colisão.
Classifique a colisão quanto à variação de energia cinética, justificando sua resposta.
Passo 1
Antes de determinar o ângulo , vamos calcular o valor do seno e do cosseno de , temos que:
elevando ao quadrado e substituindo , temos:
Logo, temos que:
Agora sim podemos determinar , para isso vamos usar a conservação de momento linear, uma vez que não atuam forças externas ao sistema:
Em , temos:
Cortando e substituindo o valor do cosseno de , temos:
Em , temos:
Dividindo por , temos:
Passo 2
Agora que sabemos o valor de , basta substituir em uma das equações achadas, se liga:
Passo 3
Para determinar o tipo de colisão, vamos analisar a variação da energia cinética:
Para a energia cinética inicial, temos:
Para a energia cinética final, temos:
Ou seja:
Por conta de a energia cinética se conservar, temos que a colisão é dita perfeitamente elástica.
Resposta
Exercício Resolvido #9
Hugh D. Young e Roger A. Freedman, Física I – Mecânica, 10a ed. São Paulo: Addison Wesley, 2003, pp – 254
Um disco de hóquei está em repouso sobre uma superfície lisa de gelo quando é atingido por outro disco de hóquei que estava inicialmente se movendo a e que passa a se mover sofrendo um desvio de da sua direção original. O disco de hóquei passa a se mover com velocidade formando um ângulo de com a direção original de . As massas dos discos são iguais. Calcule o módulo da velocidadede cada disco de hóquei depois da colisão. Qual a fração da energia cinética inicial do disco de hóquei A que foi dissipada durante a colisão?
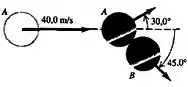
Passo 1
Temos uma colisão acontecendo, assim a primeira coisa a saber é que o momento linear do sistema é constante.
Como o disco está em repouso temos
Passo 2
Vamos começar escrevendo as velocidades iniciais dos dois discos.
Passo 3
Precisamos agora escrever as velocidades depois da colisão, como não sabemos o módulo das velocidades vamos chamá-los de e . Vamos precisar também usar a “regra do COlado/SEparado”. Para a velocidade de
Primeiro par ao eixo
E agora para o eixo
Escrevendo ela vetorialmente
Passo 4
Vamos fazer a mesma coisa com a velocidade de
Primeiro par ao eixo
E agora para o eixo
Escrevendo ela vetorialmente
Passo 5
Como as massas são iguais vamos chama-las de . Pela colisão vamos ter
Vamos ter
Passo 6
Para isso vamos ter o sistema
Pela segunda equação
Vamos substituir na primeira
Então
Passo 7
Vamos fazer a variação de energia cinética do sistema para descobrir isso
Repara que temos aquela massa perdida ali, mas ele quer a fração da energia cinética que foi dissipada, então precisamos do quanto foi dissipado e vamos dividir pela energia cinética inicial.
Eu usei o a variação de energia cinética sem sinal porque já sabemos que houve perda, ele só quer a fração então o sinal não importa.
Ele perdeu da energia cinética.
Resposta
Ele perdeu da energia cinética.