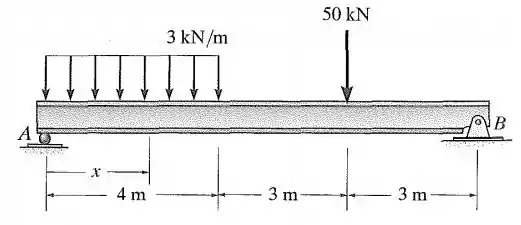
A viga está sujeita à carga mostrada na figura. Determine o deslocamento em e a inclinação em . é constante.
Passo 1
Galera essa questão já começa a misturar os tópicos de função de descontinuidade com linha elástica. Então vamos lembrar que o cálculo da linha elástica é feito como:
Vamos achar a linha elástica utilizando esse tipo de função então e calcular a deflexão e a inclinação!!
Passo 2
Vamos começar achando as reações nos apoios, para isso a gente vai fazer um desenho das forças:
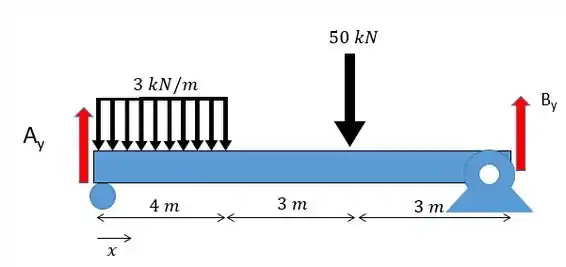
Fazendo o somatório de forças no eixo :
A força exercida pela carregamento uniforme é dada por:
Substituindo na equação:
Agora vamos aplicar o somatório dos momentos em relação ao ponto considerando o sentido anti-horário como positivo:
Lembrando que o ponto de atuação da força exercida pelo carregamento uniforme se encontra na metade do carregamento. Fica assim:
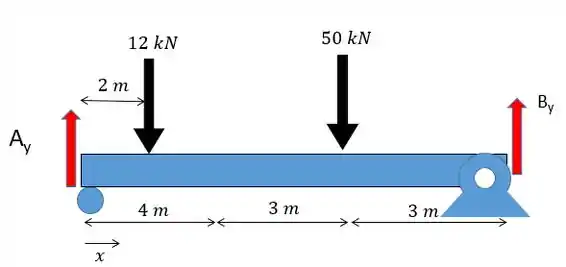
Voltando ao cálculo:
Substituindo na primeira equação vamos ter:
Passo 3
Agora temos que colocar as forças e cargas como funções de . Vamos olhar o desenho novamente:
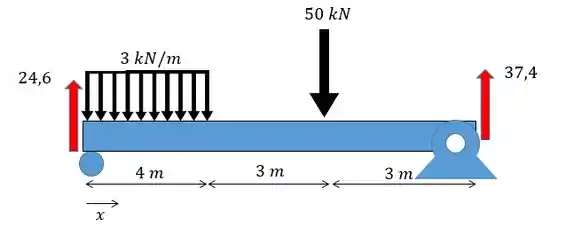
As forças aparecem como:
A carga uniforme seria dada por:
Mas perceba que se tivéssemos esse formato estaríamos considerando que essa carga atuaria desde o ponto até e não é isso que acontece!
Existe, portanto, uma falha na aplicação das funções de descontinuidade que se demonstra quando a carga não chega até o final da viga. Mas podemos resolver isso com uma combinação de cargas. Veja o esquema abaixo:
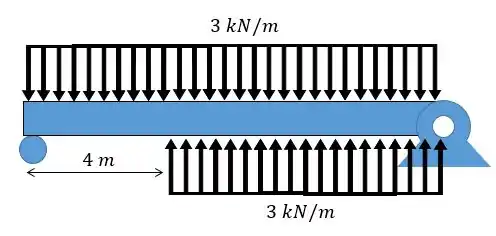
Repara que até temos apenas a carga de e depois temos uma carga de e uma de , assim, elas se anulam e voltamos a ter o carregamento que a questão pede. Portanto, a carga será dada por:
Somando os dois termos:
Passo 4
Agora vamos comçar a integrar.
A gente só tem que lembrar que quando o expoente é menor ou igual a zero a gente só precisa aumentar o expoente em uma unidade positiva! Caso o expoente seja maior do que zero então fazemos a integral normalmente.
E agora para achar o momento fletor é só integrar novamente.
Temos o momento fletor, agora é só aplicar na equação da linha elástica
Passo 5
A equação da linha elástica () é:
Então vamos integrar uma vez:
Integrando novamente:
Pronto! Achamos a equação da linha elástica, mas não temos as constantes e . Para acha-las temos de utilizar as condições de contorno!
Passo 6
Como temos um pino de um lato e um rolete de outro então em ambos os lados (tanto para quanto para ) vamos ter deflexão nula. Sendo assim vamos aplicar as duas condições à nossa equação:
- em .
- em .
Antes da gente sair substituindo em tudo a gente precisa excluir os termos que não fazem parte da nossa equação. Lembrem que é uma função de descontinuidade
Pronto! Agora substituindo e :
Como estamos na extremidade oposta não precisamos excluir ninguém.
Substituindo e
Então a nossa linha elástica é dada por:
Passo 7
Pessoal agora é só substituir , lembrando que vamos eliminar alguns termos:
Passo 8
Para a inclinação vamos ter que substituir em:
Lembrando que:
Substituindo