A matriz associada à rotação em de um ângulo no sentido anti-horário em torno da origem é:
Lembrando que o produto de matrizes representa a composição de transformações lineares, a matriz é dada por:
a)
b)
c)
d)
Passo 1
Vamos pensar em uma rotação feita várias vezes, se aplicada uma vez no vetor, ele rotaciona um ângulo , se aplicada vezes, ele vai rotacionar um ângulo
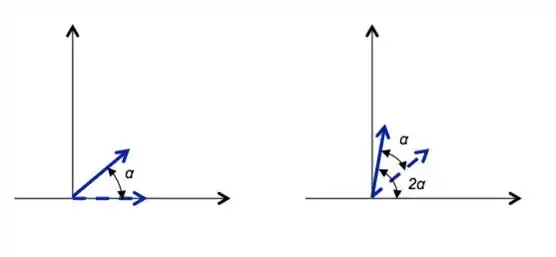
Conseguimos ver na imagem acima, na primeira, apliquei a transformação 1 vez e assim meu vetor rotacionou graus, já na segunda eu rotacionei de novo e assim ele ficou com graus do vetor rotacionado uma vez e do vetor inicial.
Dá então pra entender o que acontece quando rotaciono, 3, 4 ,5 ou até vezes! Meu ângulo passa a ser
Por isso, a matriz rotação vai ser:
Resposta
a