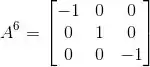A matriz
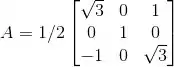
é uma rotação de radianos em torno do eixo y em Assinale abaixo a matriz .
Dica: não é uma boa ideia fazer a conta “na força bruta”,

Passo 1
Bom, a questão disse que não é uma boa ideia ficar multiplicando A por ela mesma 6 vezes.
Outra coisa que também vai dar trabalho é diagonalizar a matriz A.
Ué, então como a gente vai resolver essa questão?
Lembra que uma matriz de rotação de em torno do eixo y no é dessa forma:
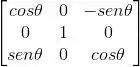
E por que eu tô lembrando disso?
Porque fazer é fazer a transformação A 6 vezes, o que significa rodar seis vezes de um ângulo de em torno do eixo y.
Isso equivale a uma única rotação de em torno de y!
Então é só substituir na matriz anterior:
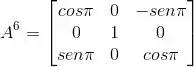
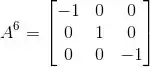
Resposta