Um bloco de massa , em repouso numa mesa horizontal sem atrito, é ligado a um suporte rígido por duas molas de constante elástica e , de modo que . Uma bala bala Juquinha, de preferência... pra quê falar de mais violência ![]()
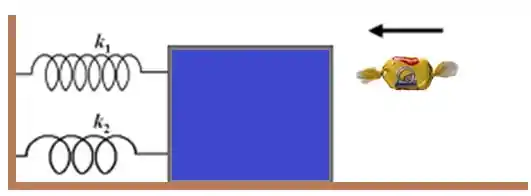
De posse dessas informações, determine a velocidade do conjunto imediatamente após a colisão e a amplitude do movimento harmônico simples associado.
(Obs.: Dica do Dexter ![]() – Confira o nosso material de associação de molas)
– Confira o nosso material de associação de molas)
Passo 1
Beleza....Vamos resolver logo essa parte da velocidade que é de boas....Vamos relembrar a conservação de momento linear para colisões que vimos lááá nas priscas eras de Física 1.
Antes da colisão, a bala Juquinha tinha velocidade e o bloco tinha velocidade nula, logo, o momento linear inicial é:
Após a colisão, tanto o bloco quanto a bala Juquinha se deslocam com a mesma velocidade
Como :
E essa é a velocidade do conjunto logo após a colisão!
Passo 2
Show de bola! Já calculamos a velocidade linear do conjunto logo após a colisão. Precisamos calcular agora qual será a amplitude do movimento oscilatório do conjunto. E aí??? Será que deu ruim??? ![]()
Sabe como vamos resolver esse problema, jovem padawan? Usando a Força? (Quem pegou a referência de Star Wars aí?)

Mais do que isso! Usaremos a Energia! Bom, mais precisamente a conservação dela ![]() .
.

Vamos considerar como início do movimento o momento em que a bala atinge o bloco. Nesse momento, a mola ainda não se comprimiu, certo? Looogo, a energia mecânica é só a energia cinética “recém-adquirida” pela colisão da bala:
Bom, e depois? Depois disso, o bloco vai comprimir a mola pouco a pouco, até que essa atinja uma compressão máxima. Essa compressão máxima será a amplitude do movimento
Belezinha... Assim, no final das contas (estamos chegando no final delas mesmo), a energia mecânica vai ser puramente energia potencial elástica:
Opa... Dexter mandou lembrar que .
Bom, como a energia se conserva, a energia mecânica inicial será igual à energia mecânica final:
Resposta
;