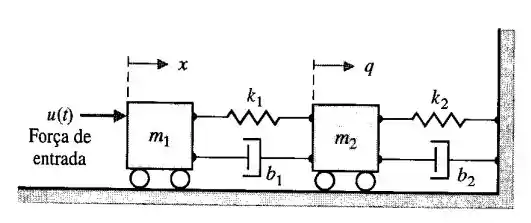
Dois carros com atrito de rolamento insignificante são conectados como mostrado na figura abaixo. A força de entrada é . Determina a equação diferencial em variáveis de estado na forma matricial.
Passo 1
Vamos escrever a equação de equilíbrio de forças para amabs as massas. Para a primeira:
Analogamente para a segunda:
Se você tover dúvida em como chegar nessas equações, seria legal dar uma revisada no conteúdo de modelos mecânicos.
Passo 2
Temos duas equações de segunda ordem, ou seja, precisamos de quatro variáveis de estado. Vamos definir a posição e a velocidade de cada uma das massas como sendo as nossas variáveis de estado:
Substituindo nas equaçõs acima:
Passo 3
Para escrever a equação diferencial de estado na forma matricial precisamos determinar o nosso vetor .
Como a velocidade é a derivada da posição, já sabemos que:
Vamos rearranjar as equações e para enxontrar e .
Rearranjando :
Rearranjando (2):
Passo 4
A partir das equações , , e podemos montar nossa equação matricial: