Um carro desce livremente por uma ladeira íngrime, com inclinação de , sem atrito. O motorista vê uma esfera cair livremente. Qual a aceleração relativa da esfera, no referencial do motorista, em termos da aceleração gravitacional?
Dica: aceleração da esfera no referencial da ladeira
Dado: .
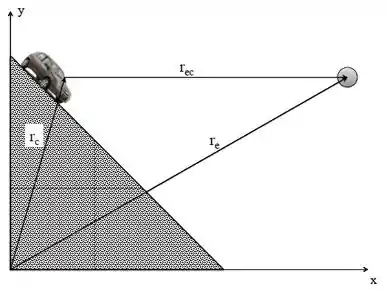
(a)
(b)
(c)
(d)
(e)
Passo 1
Essa questão é sobre movimento relativo. Queremos saber qual a aceleração da esfera com relação ao motorista do carro.
Para descobrir a aceleração da esfera com relação ao carro , é só a gente usar um outro referencial, por exemplo a ladeira parada, e calcular a aceleração da esfera menos a do carro :
Então, vamos começar achando e .
Passo 2
A questão já nos deu que a aceleração da esfera com relação à rampa é .
Faz sentido, né?
A esfera cai livremente, então, para o referencial da rampa (referencial parado), ela vai descer com a aceleração da gravidade apontando para baixo .
Até aí, tranquilo.
Passo 3
Só falta a gente achar a aceleração do carro com relação à rampa que conseguimos achar a aceleração que queremos (esfera com relação ao carro).
Para achar , a ideia é pensar na força resultante sobre o carro e a partir dela encontrar a aceleração.
Então, vamos analisar as forças que atuam no carro, lembrando de decompor as componentes da força peso :
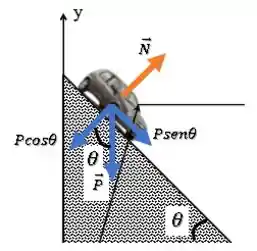
Bom, na direção perpendicula à rampa, temos uma equilíbrio:
Então, elas se anulam no cálculo da força resultante.
Sobrou apenas a componente da força peso na direção da rampa . Com isso, temos que o módulo da força resultante sobre o carro é:
Sendo que e é , então:
Passo 4
Se temos a força resultante, pela segunda lei de Newton conseguimos a aceleração:
Mas não basta só o valor em módulo, queremos também a direção do vetor .
Como a gente acha isso?
A gente sabe que a aceleração do carro está na direção da rampa, né?
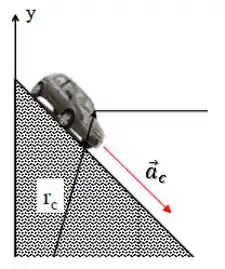
Então a gente consegue decompor esse vetor nos eixos e , lembrando que a componente em será e a componente em será . Dá uma olhada:
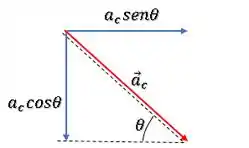
O ângulo é :
Já achamos que o valor e sabemos seno e cosseno de , então:
Passo 5
Agora que sabemos as acelerações e , basta calcular a aceleração da esfera menos a aceleração do carro que teremos a aceleração da esfera em relação ao carro:
Achamos, então, que a resposta é letra (a).
Resposta
Letra (a)