Os anéis e deslizam ao longo das hastes fixas em ângulo reto e estão conectados por um fio de comprimento . Determine a aceleração do anel em função de se o anel possui uma velocidade contante para cima .
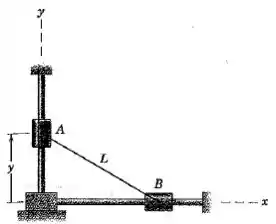
Passo 1
O sistema pode ser simplificado na seguinte figura:
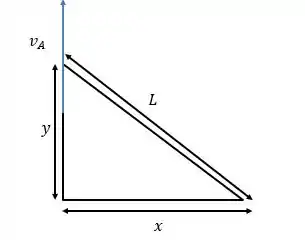
E quem é é dado por:
Passo 2
tem que satisfazer a seguinte equação:
Derivando em relação ao tempo:
E aí temos as relações das velocidades. Só que nós queremos a aceleração, né? Então, vamos derivar mais uma vez:
Sacou? Usamos a regra do produto. Simplificando:
Só que:
Por que? Porque o enunciado disse que a velocidade do anel é constante, assim a sua aceleração é nula.
E:
Então:
E quanto vale Podemos descobrir usando a primeira relação:
Passo 3
Assim:
Então:
Só que:
Passo 4
Beleza, estamos quase lá.
Lembrando que:
Assim: