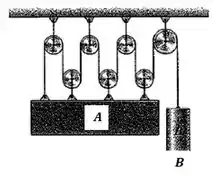
Determine a equação de restrição que relaciona as acelerações dos corpos e . Assuma que a superfície superior de permanece na horizontal.
Passo 1
O sistema é dado por:
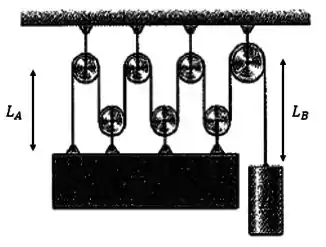
Assim, como fizemos na questão anterior, o comprimento total da corda será dado por:
é a constante que representa os comprimentos das circunferências das roldanas.
Passo 2
Assim, derivando a expressão de vamos ter que:
Derivando de novo:
E essa é a equação de restrição.