I - Um pistão com área transversal de é colocado sobre um cilindro contendo água,
conforme mostrado na figura. O cilindro está conectado a uma tubulação contendo água e
mercúrio, cuja extremidade mais externa está em contato com a atmosfera. Considerando as alturas de fluido indicadas na figura como e , determine:
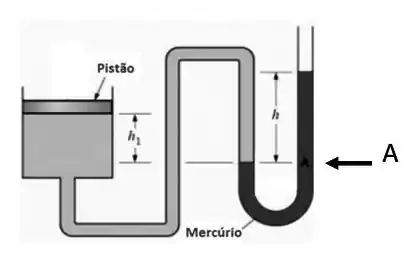
- A pressão manométrica no ponto A
- A pressão manométrica na superfície da água em contato com o pistão;
- A massa do pistão para que nenhuma força além da gravitacional seja necessária para manter o sistema nesta configuração.
Dados:
Passo 1
O segredo do sucesso nessa questão é lembrar que a pressão em um ponto de um fluido pode ser calculada por:
Onde é a pressão externa ao fluido (seja atmosférica ou causada por um peso), ρ é a densidade e a profundidade do fluido em relação à sua superfície.
E lembre-se também que para estar em equilíbrio, alturas iguais de fluidos devem ter a mesma pressão!
Passo 2
a) Pressão no ponto A.
Acima do ponto A temos uma altura de mercúrio e a atmosfera acima da superfície. Logo,
Como queremos pressão manométrica, vale lembrar que
Chegamos então que em A:
Passo 3
b) Pressão manométrica na superfície da água em contato com o pistão
Precisamos calcular a pressão na superfície da água logo abaixo do pistão. Temos acima dessa superfície: o peso do pistão e a atmosfera. Então:
Só que não temos informações sobre o peso do pistão. :(
Precisamos pensar em outra forma de resolver isso. Bom, sabemos a pressão no ponto A. Como em um líquido em equilíbrio, alturas iguais tem que ter pressões iguais!
Vamos olhar, na mesma altura de A, só que no líquido abaixo do pistão: temos o peso do pistão, a pressão atmosférica, e uma altura de água.
Já a pressão manométrica na altura de A
A pressão que queremos é a do pistão, logo
Como já calculamos a pressão manométrica na altura de A
Passo 4
c) Qual a massa do pistão?
Como vimos no último passo, para o sistema ficar em equilíbrio, o pistão tem que fazer uma pressão . Lembrando que
Então, no pistão: