No sistema abaixo, sabe-se que . Determinar a densidade do líquido.
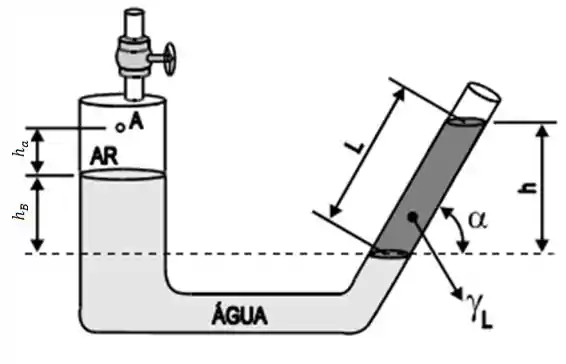
São dados:
Considere e
Passo 1
Queremos encontrar a densidade do líquido à direita.
Para isso, aplicamos o Princípio de Stevin: igualamos as pressões de um mesmo fluido a uma mesma altura.
Neste caso, vamos igualar as pressões nos pontos (1) e (2), que correspondem à interface entre os fluidos no lado direito e o ponto correspondente no lado esquerdo:
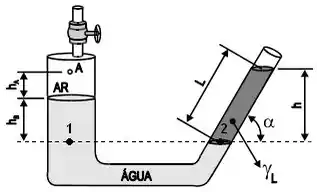
Logo:
Passo 2
Vamos calcular as pressões e :
Calculando :
onde e são dados e é a densidade da água:
Convertendo para metros:
Observe que .
Convertendo para :
Calculando :
onde é a densidade do líquido, é a pressão atmosférica e é dado do problema.
Convertendo para metros:
Passo 3
Igualando as pressões:
Passo 4
Substituindo os valores: