Introdução à Estatística
Teoria
A estatística é uma ciência de análise de dados. Aqui aprendemos a como coletar, organizar e analisar dados de forma que a gente possa tirar conclusões corretas a partir deles! Pensa aí nas pesquisas eleitorais, na análise de qualidade da água…o que mais tem é exemplo! 😉
Mas antes de entrar de cara no mundo dos dados a gente precisa de uma introdução à estatística pra aprendermos conceitos super importantes! Então se liga nesse vídeo super completo! 👇
📢 Clique para ver mais:
População e Amostra
População e Amostra são parâmetros super importantes da estatística! A população é todo o sistema da onde você quer obter uma informação, já a amostra é um pedaço dessa população que vai te dar a resposta!
Por exemplo, você vai fazer um exame de sangue e pra isso vão espetar uma agulha no seu braço e tirar um pouquinho de sangue. Esse sangue é a amostra!
-E quem seria a população?! 😖
A população nesse caso é todo o sangue do seu corpo! 😱 Entendeu a importância da Estatística?! 😍
Tipos de Variáveis
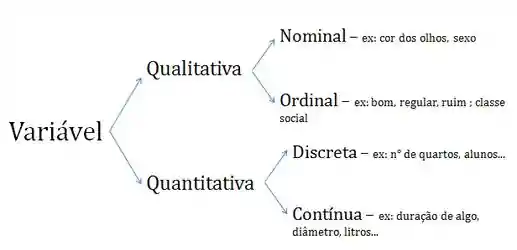
Quando fazemos um levantamento de dados, sempre estamos analisando uma variável. Seja ela numérica ou não! As variáveis podem ser divididas em dois grandes grupos, as variáveis qualitativas e quantitativas.
Vamos conhecer elas melhor!
Variável Qualitativa
Como o próprio nome diz, essa amostra não envolve números! Ela pode ser dividida em outros dois tipos:
- Variável Nominal: Descreve informações como, cor dos olhos, sexo, etnia, etc.
- Variável Ordinal: Por exemplo, bom, regular e ruim.
Variável Quantitativa
A variável quantitativa trás uma informação numérica, ela tambpem pode ser dividida em dois grupos:
- Variável Discreta: têm um número contável de valores entre quaisquer dois valores, como por exemplo número de alunos e número de cômodos de uma casa.
- Variável Contínua: têm um número infinito de valores entre dois valores quaisquer, como por exemplo uma medida, a duração de algo em tempo, o volume em litros, etc.
Se liga nesse resuminho de tipos variáveis:
Teoria da Amostragem
A teoria da amostragem nada mais é do que estudar as relações entre uma população e as amostras que são extraídas dela! Muitas vezes a gente não conhece algumas grandezas, que chamamos de parâmetros, da população (média, variância, proporção,...). Mas a gente pode estimar esses parâmetros através das nossas amostras!
Cada grandeza populacional tem a sua respectiva estatística amostral. Por exemplo, a média populacional
Tipos de Amostragem
Existem algumas formas de selecionar uma amostra. Por exemplo, podemos escolher 10 lápis numa caixa com 100 lápis ou podemos ter uma amostra de pessoas voluntárias a fazer um teste específico. Vamos conhecer os tipos de amostragem probabilísticos!?
- Amostragem Aleatória Simples: como o nome já diz, a gente enumera a população e vai sorteando, com reposição, até a gente ter nossa amostra completa.
- Amostragem Sistemática: N é o tamanho da população e a amostra deve ter tamanho n. Nesse caso a amplitude do intervalo de amostragem é a razão entre o tamanho da população e o tamanho da amostra;
- Amostragem Estratificada: Acontece quando a nossa população pode ser dividida em subpopulações. Aí na hora de selecionar a amostra, teremos que escolher de forma igualmente proporcional elementos de todas as subpopulações.
Número de Amostras
O número de amostras possíveis para uma população depende se a extração é feita com ou sem reposição! No caso de extração com reposição, fazemos:
E no caso de extração sem reposição, fazemos:
Agora vamos praticar com exercícios!
Teoria da Amostragem
Exercícios Resolvidos
Exercício Resolvido #1
PUCRIO-P1-2011.2-1a)
- Defina população e amostra. Dê exemplos.
Passo 1
Esses conceitos são realmente muito importantes...
População seria um grupo formado por todos os elementos cujas características a gente quer conhecer e amostra seria um subconjunto desse grupo, no qual podemos medir essas características para estimar as características da população.
Um exemplo muito simples é o da eleição.
População seria, por exemplo, todos os brasileiros que votam e decidem a eleição. Amostra seria o grupo de brasileiros entrevistados pelo Ibope ou coisa do tipo.
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
CEFET -Prof Anna Regina
Um administrador hospitalar faz uma pesquisa com as pessoas que estão na fila de espera para serem atendidas pelo sistema SUS.
- Se para realizar esta pesquisa, o administrador resolve entrevistar uma a cada 10 pessoas da fila, que tipo de amostragem ele realizou?
- As pessoas desta fila foram divididas em três grupos, de acordo com sua doença, cujos tamanhos são, respectivamente, e sabendo que, ao ser realizada uma amostragem estratificada, nove elementos da amostra foram retirados do terceiro grupo, determine o número total de elementos da amostra, ou seja, o número total de pessoas entrevistadas.
Passo 1
(a)
Se eu pego 1 a cada 10, eu to mantendo uma amplitude na minha amostragem, concorda? De 10 em 10.
Isso significa que estamos com uma amostragem sistemática.
Passo 2
(b)
Agora dividimos nossa população (pessoas da fila), em 3 estratos:
O problema diz que 9 pessoas foram entrevistadas do terceiro estrato, e pergunta o número total de entrevistados.
Passo 3
A gente sabe que numa amostragem estratificada a gente tem que manter a proporção em todos os estratos, então..
Isso significa que se eu tirei 15% do terceiro, vou ter que tirar 15% dos outros dois estratos também.
Passo 4
Primeiro..
Segundo...
O número total de entrevistados será:
Resposta
Exercício Resolvido #3
CEFET -Prof Anna Regina
Uma população se encontra dividida em três estratos, com tamanhos, respectivamente, , e . Ao realizar uma amostragem estratificada proporcional, doze elementos da amostra foram retirados do primeiro estrato. Qual o número total de elementos da amostra?
Passo 1
O problema trata de uma amostragem estratificada, beleza?
Lembra que nesse tipo de amostragem, nossa população está dividia em subpopulações ou estratos. Nesse caso, são:
Passo 2
Temos que lembrar que ao tirar a amostra, mantemos a mesma proporção em todos os estratos.
Isso quer dizer que se eu tirei 12 do primeiro estrato...
Então eu tenho que tirar 15% do segundo e do terceiro.
Passo 3
Segundo estrato:
Terceiro estrato:
O número total de elementos da amostra será:
Resposta
Exercício Resolvido #4
Elaboração Própria
Suponha que temos uma população de elementos, e queremos montar uma amostra usando um elemento a cada elementos da população, a partir do elemento. Que tipo de amostragem devemos fazer? Qual deve ser a nossa amostra?
Passo 1
A questão tá pedindo uma amostragem sistemática, certo? Está nos dando o tamanho total da população e pedindo uma amostra usando um elemento a cada , ou seja, é a nossa amplitude! Lembrando da fórmula
Como e ...
Nossa amostra tem que ter elementos!
Passo 2
Começando do elemento, como foi pedido, nossa amostra seria:
Sempre somando , nossa amplitude, à posição do elemento anterior!
Resposta
Exercício Resolvido #5
Elaboração Própria
João, professor de probabilidade, está realizando uma pesquisa e gostaria de calcular o número de amostras possíveis que se pode obter a partir de uma população de 20 elementos se quisermos montar uma amostra aleatória com elementos sem reposição.
Passo 1
Vamos lááá!!!
O enunciado nos diz que temos uma população de 20 elementos e a partir dela queremos calcular o número de amostras que podemos ter se quisermos montar uma amostra aleatória com 15 elementos sem reposição! Repito: SEM REPOSIÇÃO! haha
Para calcular isso utilizaremos a fórmula de combinação:
Onde
Beleza... No caso aqui queremos calcular 15 elementos para montar uma amostra aleatória de um total de 20 elementos. Ou seja, combinação de 15 elementos de 20!!
Passo 2
Substituindo os valores, temos
Abrindo os fatoriais do numerador e denominador, ficamos com
Opa!! Podemos cortar o do numerador com o do denominador:
Portanto, fazendo as continhas com o que sobrou, temos
Ou seja, conseguimos obter amostras com 15 elementos sem reposição! Beleza?!