Variável Aleatória Discreta
Teoria
Uma variável aleatória é discreta quando o conjunto de valores que ela pode assumir for um conjunto enumerável e finito. Por exemplo, qual é a probabilidade de jogar um dado e cair o número 6?
Nesse caso sabemos que o dado pode assumir os valores
📢 Clique para saber mais:
- Variável aleatória discreta: Exercícios Resolvidos
- Introdução à Variável Aleatória Contínua
- Medidas de Centralidade e Dispersão para V.A. Discreta
Exemplo: Duas moedas são lançadas de forma independente, qual é a probabilidade de sair pelo menos uma cara?
Nesse exemplo a variável aleatória discreta vai ser a quantidade de vezes que pode sair cara nesse experimento! Bora ver como isso funciona? 👇
Passo 1: Escrever o espaço amostral
Aqui a gente vai escrever todas as possibilidades de resultado, vamos considerar
Ou seja, pode sair:
- Cara nas duas moedas;
- Cara na primeira e coroa na segunda;
- Coroa na primeira e cara na segunda ou
- Coroa nas duas moedas
Você também pode conferir esse conteúdo em vídeo:
Passo 2: Identificar a variável aleatória discreta
Vamos chamar a variável aleatória discreta de
Passo 3: Calcular a Probabilidade de Cada Variável Aleatória
A probabilidade de
Montamos uma tabelinha com a quantidade de caras que pode sair nos lançamentos e a probabilidade de cada possibilidade.
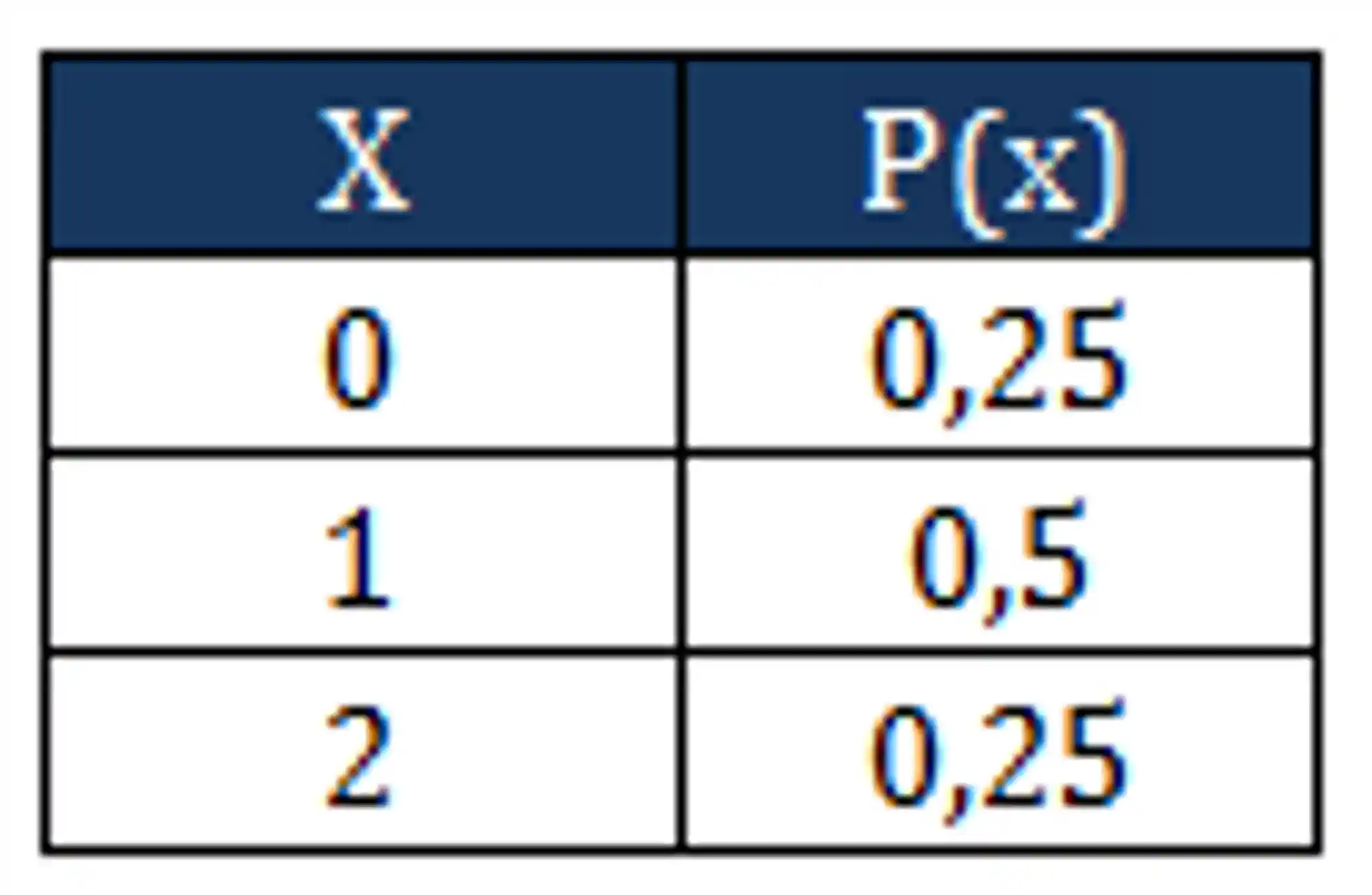
Passo 3: Calcular a Probabilidade de
Nesse caso somamos a probabilidade de cair apenas uma cara, com a probabilidade de caírem duas caras.
Ou seja, a probabilidade de cair pelo menos uma cara é igual a
Agora vamos praticar com mais exercícios?
Exercícios Resolvidos
Exercício Resolvido #1
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 1
Considere uma urna contendo três bolas vermelhas e cinco pretas. Retire três bolas sem reposição, e defina v.a. X igual ao número de bolas pretas. Obtenha a distribuição de X.
Passo 1
Vamos lá! Temos ao todo 8 bolas, sendo:
3 vermelhas e 5 pretas
Tirando três bolas sem reposição, podemos ter (lembrando que a v.a. conta o número de bolas pretas retiradas):
Certo?
Vamos calcular a probabilidade de cada um desses casos:
Passo 2
1º caso:
O único jeito de termos três bolas pretas é:
Pra calcular essa probabilidade, vamos fazer da seguinte forma:
Pra primeira bola retirada, temos 5 pretas de um total de 8 bolas, então a probabilidade de a primeira ser preta será de
Agora, já tendo retirado a primeira bola e ela sendo preta, temos 4 bolas pretas de um total de 7 bolas, então a probabilidade de a segunda bola ser preta agora é de
Usando o mesmo raciocínio, pra terceira bola temos que a probabilidade será de
Agora é só multiplicar tudo (queremos a probabilidade da primeira ser preta e a segunda ser preta e a terceira ser preta):
Passo 3
2º caso:
Agora vai mudar um pouquinho a conta. É o seguinte: pra gente ter duas bolas pretas, concorda que os resultados possíveis são
Calculando a probabilidade de cada um deles que nem no passo anterior, temos o seguinte:
Agora é só somar os três (podemos ter duas bolas pretas ou do primeiro jeito ou do segundo ou do terceiro):
Passo 4
3º caso:
As possibilidades para termos 1 bola preta são:
Fazendo o mesmo raciocínio do passo anterior, temos:
Passo 5
4º caso:
Agora a única possibilidade é
Calculando da mesma forma que no passo 2:
Passo 6
Então a distribuição de X será:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #2
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 135-02
Considere uma urna contendo três bolas vermelhas e cinco pretas. Retire três bolas, com reposição, e defina a v.a. X igual ao número de bolas pretas. Obtenha a distribuição de X.
Passo 1
O que o enunciado quer? A distribuição de X, que ele definiu como uma variável aleatória igual ao número de bolas pretas da nossa extração. Podemos ter:
Vamos olhar cada caso melhor?
Passo 2
1º caso: Nenhuma bola preta
Nesse caso, teríamos:
Temos três bolas vermelhas de um total de 8 bolas. A probabilidade da primeira bola ser vermelha então é de .
Como estamos repondo as bolas retiradas, a probabilidade de a segunda ser vermelha também é de
Mesma coisa para a terceira bola!
Então a probabilidade de as três bolas serem vermelhas é dada pela multiplicação:
Passo 3
2º casoApenas uma bola preta
As possibilidades para termos 1 bola preta são:
Vamos calcular a probabilidade de cada caso usando o mesmo raciocínio do passo 2 (tomando cuidado porque temos 5 bolas pretas de um total de 8, então a probabilidade de tirar uma preta é ):
Somando as três probabilidades, temos:
Passo 4
3º caso: Duas bolas pretas
Esse caso é super parecido com o 2º. As possibilidades são:
Calculando do mesmo jeito, temos:
Passo 5
4º caso: Três bolas pretas
Esse caso é parecido com o 1º só que agora com as bolas pretas.
Passo 6
Montando a tabela de distribuição de X:
Resposta
Exercício Resolvido #3
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006, 135-03
Suponha que uma moeda perfeita é lançada até que cara apareça pela primeira vez. Seja X o número de lançamentos até que isso aconteça. Obtenha a distribuição de X. (Observe que, nesse problema, pelo menos teoricamente, X pode assumir um número infinito de valores.)
Passo 1
Vamos lançar moedas até dar cara, ou seja, enquanto der coroa continuamos a jogar.
Podemos ter as seguintes possibilidades:
Note que não temos um limite para X, então calcularemos até certo ponto apenas.
Passo 2
1º caso: (K) Conseguimos K na primeira tentativa.
2º caso: (CK) Conseguimos K na segunda tentativa
Perceba que aqui nós multiplicamos as probabilidades de quando dá C e quando dá K. Fazemos isso pois são eventos sucessivos, ocorrem um atrás do outro
3º caso: (CCK) Conseguimos K na terceira tentativa
...
N-ésimo caso: (CCC..CK) Conseguimos K na n-ésima tentativa
Passo 3
Construindo a tabela de distribuição de X:
Resposta
Exercício Resolvido #4
Pedro A. Morettin e Wilton de O. Bussab, Estatística Básica, 5ª ed. São Paulo: Saraiva, 2006
Considere o lançamento de três moedas. Se ocorre o evento, dizemos que temos uma sequência, ao passo que se ocorre o evento temos três sequências. Defina a variável aleatória = número de caras obtidas e = número de sequências, isso para cada resultado possível. Assim, e . Obtenha as distribuições de e .
Passo 1
Vamos entender primeiro um pouco melhor essas variáveis e ?
Vamos listar todos os possíveis resultados que podemos obter no lançamento de três moedas, chamando cara de e coroa de
Temos então oito iresultados! Cada um deles tem portanto , ou, de probabilidade de acontecer.
Passo 2
Para cada um dos possíveis casos, a variável será a quantidade de caras obtidas e o número de sequências consecutivas. Mas o que é uma sequência consecutiva?
Sempre que tivermos resultados iguais que aconteceram um após o outro, estaremos em uma sequência, mesmo que nessa sequência só tenha um resultado.
Por exemplo, na sequência , temos três sequências consecutivas, uma para o primeiro , uma para o e uma para o último . Já no caso, teríamos duas sequências, uma para o e uma para o . Por fim, no caso , aí teríamos apenas uma sequência.
Para todos os casos, temos a seguinte tabela:
Beleza?!
E agora podemos listar as probabilidades de cada ou acontecerem também! Como?
Por exemplo, quando temos , ou . Então:
Seguindo o mesmo raciocínio para o , teríamos, por exemplo:
Show de bola?!
Resposta
