Quando uma carga constante é aplicada a uma longa coluna delgada de seção transversa uniforme e comprimento , a coordenada de um ponto de sua curva de deflexão é dada por
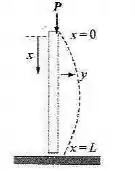
Onde as constantes são, respectivamente, o módulo de Young e o momento de inercia da seção transversa. Veja a figura. Se a coluna é impedida de rotar em seu topo e em sua base, as condições de contorno são e .
a) Mostre que esse problema de valores de contorno indica que a coluna não verga, a menos que a carga tenha um dos valores Essas diferentes cargas são chamadas de cargas críticas.
b) Mostre que a curva de deflexão correspondente à mais baixa carga crítica , chamada carga de Euler, é Então é chamado primeiro modo de deformação.
Passo 1
Vamos pensar um pouco no que a gente vai fazer antes de sair cuspindo matemática. Quando a gente resolve um problema de valor de contorno nós procuramos soluções não triviais. No nosso problema, se resolvermos como um problema de valor de contorno nós vamos encontrar os valores de que fazem não ser uma solução trivial, ou seja, os valores onde a barra enverga.
Vamos manipular a equação e escrever como um problema de valor de contorno.
Passo 2
a) Agora temos que resolver o sistema pra mostrar o que ele tá pedindo. Vamos montar a equação característica.
Passo 3
Caso
Quando temos uma raiz dupla nós já sabemos que a solução vai ter essa cara.
Como
Passo 4
Vamos usar os valores iniciais para descobrir se esse caso nos dá soluções não triviais.
Como
Logo . Então esse caso só nos deu uma solução trivial
Passo 5
Caso
Teremos duas raízes distintas e reais iguais a.
E a solução vai ter a seguinte cara.
Passo 6
Vamos usar os valores iniciais para descobrir se esse caso nos dá soluções não triviais.
Para que o termo dentro do parênteses fosse igual a zero teríamos que ter , o que é um absurdo dada a nossa condição de . Sendo assim temos.
O que nos dá outra solução trivial.
Passo 7
Caso
Nesse caso iremos ter duas raízes complexas que serão
Então a nossa solução vai ter a seguinte cara.
Passo 8
Vamos usar os valores iniciais para descobrir se esse caso nos dá soluções não triviais.
Disso ou nós teremos , que nos dá outra solução trivial, ou . Como nós não queremos uma solução trivial vamos testar o segundo caso. Como sabemos das propriedades do seno.
Logo teremos como valores de
Que é exatamente o que queríamos mostrar na letra a.
Passo 9
b) Nesse item ele quer que a gente mostre a solução da equação para . A gente já sabe que.
Manipulando um pouco nós teremos.
A gente já sabe dos itens anteriores que a nossa solução tem a seguinte cara.
Renomeando a nossa constante e substituindo teremos.
Que é a solução do item b
Resposta
Ei, a resposta está no passo a passo :)