Exercícios de Problemas de Autovalor - Lista de Exercícios Resolvida

Determine os autovalores e as autofunções do problema de contorno dado.

Determinar para quais valores de o seguinte problema de valor de contorno admite soluções não triviais (não identicamente nulas):

Quando uma carga constante é aplicada a uma longa coluna delgada de seção transversa uniforme e comprimento , a coordenada de um ponto de sua curva de deflexão é dada por

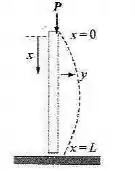
Onde as constantes são, respectivamente, o módulo de Young e o momento de inercia da seção transversa. Veja a figura. Se a coluna é impedida de rotar em seu topo e em sua base, as condições de contorno são e .

a) Mostre que esse problema de valores de contorno indica que a coluna não verga, a menos que a carga tenha um dos valores Essas diferentes cargas são chamadas de cargas críticas.

b) Mostre que a curva de deflexão correspondente à mais baixa carga crítica , chamada carga de Euler, é Então é chamado primeiro modo de deformação.

Determinar para quais valores de o seguinte problema de valor de contorno admite soluções não triviais (não identicamente nulas):

Encontre as autofunções e autovalores do problema

Supondo encontre as soluções do problema

Estudando os 3 casos, , , .

Supondo , determine todos os autovalores reais as respectivas autofunções do problema de valor de contorno abaixo.

Determine todos os valores de (e todas as soluções correspondentes), para os quais existem soluções não-nulas do problema de valor de contorno:

Encontre as autofunções e autovalores do problema

(Dica: use a equação de Euler)

(I)Encontre todos os valores de e todas as soluções associadas, para os quais existem soluções não-nulas do problema de valor de contorno

(ii) Para quais valores de , não existe nenhuma solução não-trivial do problema de contorno

Para qualquer valor de

Encontre todos os valores de para os quais existem soluções não triviais da seguinte equação de Euler com condições de contorno.

Quais são as soluções não triviais?

Determine todos os valores de para os quais o seguinte problema de EDO com condições de contorno tem ao menos uma solução diferente de zero.

4- Na solução do problema de Valor inicial e de Contorno para a equação do calor numa barra de comprimento com condições de contorno , para todo (barra isolada numa extremidade e mantida a zero graus na outra), pelo método de separação de variáveis, precisamos resolver o seguinte problema de autovalores e autofunções:

Determine uma sequência de autovalores e autofunções associados para este problema, ou seja, encontre uma sequência de funções não nulas tais que , para todo , e .

Encontre todos os valores de para os quais existe ao menos uma solução não nula do problema de valor de contorno

Escolha uma opção:

a) , com inteiro

b) , com inteiro

c) para nenhum valor de

d) e

Resolva o seguinte problema de autovalores (Obs.: todas as possibilidades de devem ser analisadas.)

Encontre as autofunções e autovalores do problema

(Dica: use a equação de Euler)

Encontrar os valores de pelos quais o seguinte problema tem solução não trivial.

Escolha uma opção:

a) Nenhum

b)

c)

d)

e)

Determine todos os valores de para os quais o seguinte problema de EDO com condições de contorno tem ao menos uma solução não trivial.