Para uma malha de realimentação representada pelo diagrama de blocos abaixo:
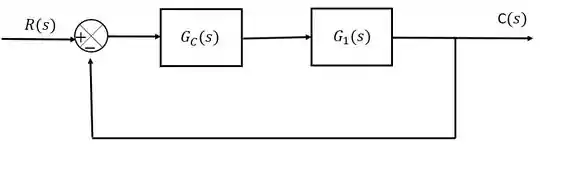
Determine o ganho e período finais para um controlador proporcional para a função de transferência de processo abaixo:
Passo 1
Como a malha que estamos trabalhando é do tipo feedback, a função de transferência equivalente da malha é:
Para o método da substituição direta, o que tilizamos é a equação característica da malha, que nada mais é que o denominador da função de gransferência queivalente, ou seja, a nossa equação característica é:
Passo 2
O nosso controlador é do tipo proporcional, portanto sua função de transferência será:
E a do processo:
Colocando tudo na equação característica:
Multiplicando tudo pelo denominador:
Passo 3
Aplicando a nossa famosa substituição:
Como:
Separando a parte real da imaginária e igualando as duas a :
Da parte imaginária temos:
Substituindo na expressão da parte real:
Substituindo o valor de :
Para determinar o períofo final, devemos aplicar a fórmula:
Logo: