Para uma malha de realimentação representada pelo diagrama de blocos abaixo:
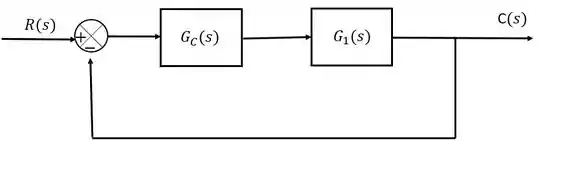
Determine o ganho e período finais para um controlador proporcional para a função de transferência de processo abaixo:
Passo 1
Como a malha que estamos trabalhando é do tipo feedback, a função de transferência equivalente da malha é:
Mas nós estamos interessados na equação característica, que nada mais é do que o denominador da função de transferência. Sendo assim, nossa equação de transferência para esse caso será:
Passo 2
Como estamos trabalhando com um controlador proporcional, a função de transferência para o controlador será:
Porém, aqui esbarramos com um problema. A função do processo tem um termo exponencial: o famoso tempo morto.
Sempre que precisarmos fazer substituição direta em uma função de transferência com tempo morto nós acionaremos o nosso megazord chamado aproximação de Padé.
Relembrando a fórmula da aproximação de Padé:
Para o nosso exercício então:
A nossa função de transferêncua para o processo será então:
Colocando tudo na equação característica:
Multiplicando tudo pelo denominador:
Passo 3
Hora de aplicar nossa substituição:
Como:
Agora, já sabe né, devemos separar a parte real da imaginária e igualar as duas a :
Da parte imaginária temos:
Da parte real:
Para determinar o períofo final, devemos aplicar a fórmula:
Logo: