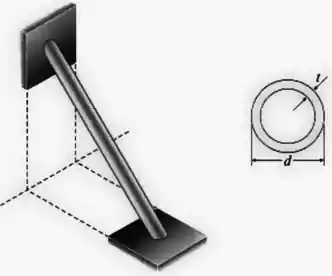
Um tubo de alumínio servindo de braço na fuselagem de um pequeno avião (veja a figura) é dimensionado para resistir uma força de compressão. O diâmetro externo do tubo é e a espessura da parede é . A tensão de escoamento para o alumínio é e a tensão última é .
Calcule a força de compressão admissível se os fatores de segurança em relação à tensão de escoamento e à tensão última são e , respectivamente.
Dica do Expert: A “tensão de escoamento” e a “tensão última” se referem a dois tipos de falha diferentes (deformação irreversível e ruptura, respectivamente) causados por tensão normal.
Vai importar para o cálculo de o tipo de falha que tiver a menor tensão normal admissível .
Passo 1
A figura do exercício nos confunde quando mostra a barra inclinada, mas isso não faz diferença! Se formos ler o enunciado, vemos que a única força nessa barra é a compressão.
Bom... O exercício quer saber qual é a força máxima de compressão que pode ser feita no tubo de forma a gerar uma tensão normal média que ainda satisfaz a condição:
Para resolver o exercício, precisamos encontrar (em função da força ) e . Substituindo esses dois valores na expressão acima, vamos poder isolar e descobrir qual é seu valor máximo.
Para encontrar a tensão normal média , vamos usar sua fórmula:
Como o tubo está sob compressão por uma força , então a força normal interna vai ser igual à .
A área da seção transversal do tubo, por sua vez, vai ser um pouco mais difícil de calcular. Ela vai ser a diferença entre a área de dois círculos, um de diâmetro e outro de diâmetro .
Do enunciado temos que e . Se chamarmos o diâmetro do círculo menor de , podemos já deixa-lo calculado:
Já para encontrar a tensão normal admissível , vamos calculá-la para os dois tipos de falha usando a fórmula:
A tensão admissível do projeto como um todo vai ser a menor tensão admissível entre os dois tipos de falha.
Isso porque se a gente garantir que a tensão não ultrapassa a menor tensão admissível, estamos garantindo também que ela não vai ultrapassar a maior tensão admissível.
Do enunciado, temos que:
- Para a falha por escoamento (deformação irreversível), e ;
- E para a falha por tensão última (ruptura), e .
Passo 2
Então vamos começar encontrando a tensão normal admissível .
Para a falha por escoamento/deformação irreversível, temos:
Substituindo os valores do enunciado:
E para a falha por tensão última/ruptura temos:
Substituindo os valores do enunciado:
Como é menor, essa vai ser a nossa tensão normal admissível:
Passo 3
Agora vamos encontrar a tensão normal média :
Como o tubo está só sob compressão por uma força de intensidade , então a força normal interna é igual à .
Quanto à área , ela é a diferença entre as áreas de dois círculos de diâmetro e :
Tirando em evidência:
Substituindo os valores encontrados na fórmula da tensão normal média:
Passo 4
Finalmente, aplicamos a condição de projeto:
Substituindo a expressão encontrada para no passo anterior:
Isolando :
Substituindo os valores , e :
Se calcularmos a expressão da direita e lembrarmos que , isso dá:
Esse número é um pouco grande, então podemos reescrevê-lo em para a resposta: