Interpolação por Sistema Linear
Produzido por Bruno PestanaTeoria
Introdução
Faaaaalaa aí meus caros, tudo certinho? Vamos começar a falar de um assunto muito usado em V-Á-R-I-A-S matérias...

Se prepara então, que estamos entrando em Interpolação! Mas, na real... tu sabes o que é interpolar?
Podemos citar diferentes exemplos, tipo na física 1, quando estamos estudando a variação da posição percorrida por um carro em relação ao tempo. Geralmente conseguimos uma série de pontos de tempo (eixo x) e a posição (que varia em função do tempo), com esses valores podemos montar gráficos, tabelas e etc.
Então, a primeira informação que sabemos é que temos uma série de pontos:
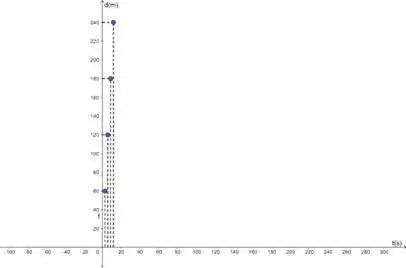
Perceba o que temos aqui, uma série de valores numéricos de uma função, e esses valores me dão vários conjuntos de pontos, mas e se nós quisermos calcular um valor não tabelado? Imagine que nosso fusquinha está andando (pensa num fusca rápido).
Qual é a posição percorrida em 5 segundos? Nesse caso é fácil né, olhando no gráfico, é fácil inferir que o valor está crescendo de forma linear e que a cada 3 segundos o fusquinha anda 60 metros (PASME!). E encontrando a função vemos que .
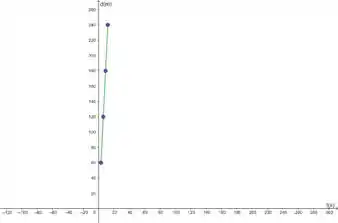
Mas e se a solução não for tão óbvia assim? Aí o bicho pega! Como é que eu vou adivinhar ? Sem condições pra isso parceiro!
Então... veja bem, eu disse lá em cima que na interpolação nós precisamos de um conjunto de pontos. Basicamente o que acontece é: se qualquer função definida e contínua dentro de um intervalo. EXISTE um polinômio () muuuuuuuuito próxima da função real (). Deu pra pescar a ideia?
Mesmo em casos que nós já conhecemos a função, é bem interessante encontrarmos uma interpolação simples de derivar e integrar, já que derivar polinômio é moleza!
E como fazemos isso?
Bom, vamos começar com uma definição importante. é uma função de interpolação de grau de se para pontos conhecidos (chamados nós de interpolação), temos:
Nós tiramos duas coisas daí. Primeiro que o valor da interpolação nos nós é o mesmo da função nos nós. Até aí tudo bem né? A segunda coisa é que precisamos de nós para encontrarmos um polinômio de grau . Sabe aquela história de que precisamos de pontos para determinar uma parábola (grau )? Então, é a mesma ideia, só extrapolamos para graus maiores.
Voltando, um palpite simples e que pode trazer bons resultados é ligar os pontos por uma reta, por exemplo. Imagine que queremos encontrar . Onde e queremos interpolar no intervalo .
Como , se aproximarmos nossa para uma reta, temos que . Substituindo o valor na função de fato temos . Não foi nenhuma maravilha de aproximação, mas não foi um erro tão grande né? Vou fazer um desenho pra você visualizar melhor o que a gente fez agora:
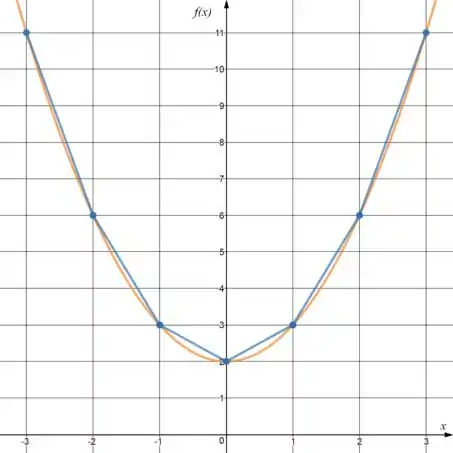
Temos que a linha laranja é a nossa função, os pontos azuis são os pontos que conhecemos e as linhas azuis representam a aproximação linear que a gente fez. Deu pra ver que a aproximação é realmente razoável né?
Esse método, no entanto, é bem limitado e muito pouco confiável como podemos ver no exemplo abaixo com a função :
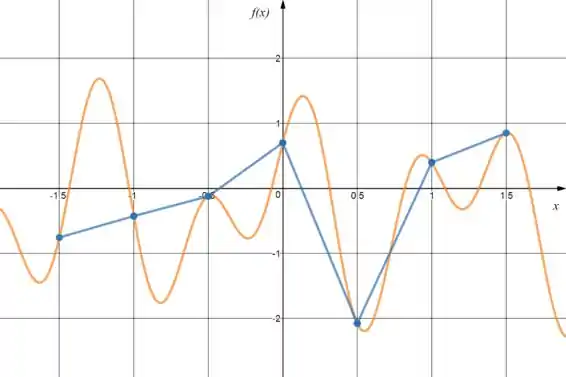
Deu bem longe né? Mas, de acordo com nossa definição, essa aberração azul aí é uma função de interpolação! Só não é uma muito boa haha. Então agora que já sabemos com o que estamos lidando vamos aos métodos!
Interpolação Polinomial
Uma das interpolações mais conhecidas é a Interpolação Polinomial, basicamente vamos pegar um conjunto de pontos e transforma-los em um polinômio, também existem outras formas de interpolação como a exponencial e a trigonométrica.
Sendo assim, pode ser escrita como:
E também sabemos que , para todo de a . Então, podemos escrever o sistema:
Passando pra forma de matriz ficamos com:
Veja bem, se todos os pontos forem diferentes, nosso sistema terá uma solução única.
Ou seja, existe apenas um polinômio de grau que interpola nos pontos conhecidos e a nossa solução vai ser tãooooo próxima quanto quisermos!
E a primeira forma de achar esse polinômio nós acabamos de ver aqui haha. É só resolver esse sistema! Vamos ver um exemplo:
Encontre o polinômio que interpola os pontos da tabela abaixo:
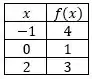
Jogando esses pontos num gráfico, temos:
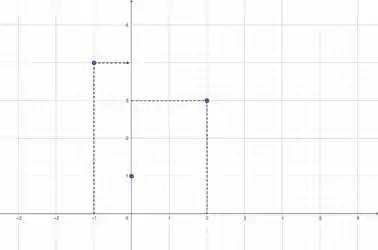
Como temos nós de interpolação, nosso polinômio será de grau (já que para um polinômio de grau , temos pontos):
Para que interpole precisamos que:
Jogando numa matriz, teríamos:
Então ficamos com:
Substituindo na equação :
Substituindo e a expressão para na equação :
Substituindo na equação :
Logo, temos que:
Vamos ver como fica esse polinômio junto com os pontos? Fica assim:
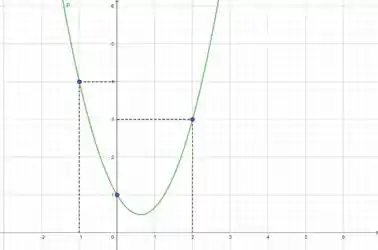
Ele representa bem os pontos dados!!
Bem tranquilo né? O único cuidado que precisamos ter aqui é com a nossa matriz de coeficientes. Lembra que nos métodos de solução de sistemas lineares tínhamos uma série de problemas como, por exemplo, o pivô ser zero ou próximo de zero?
Então imagina se sua matriz de coeficientes só tiver números próximos de zero! Tipo assim:
Nós provavelmente não chegaríamos a uma função de interpolação devido aos problemas nos métodos de solução de sistemas lineares. Mas relaxa que vamos nos preocupar com isso mais pra frente haha.
Algoritmo
Achou que ia ter algum algoritmo? Relaxa, era só isso mesmo. Basicamente nós resolvemos sistemas lineares.
O que nós fazemos é pegar o nosso conjuntinho de pontos (os nós de interpolação) e transforma-los em um sisteminha. Bora fazer exercício!