Parábolas
Teoria
O que são cônicas?
Lembra no colégio quando estudamos as equações de segundo grau? Por exemplo, essa equação aqui
é uma equação do segundo grau, concorda?! Vamos tentar entender aqui um pouco melhor o que elas significam e a utilidade delas, show de bola?!?!
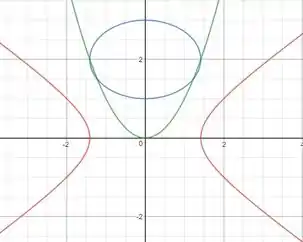
Então vamos lá! Por acaso você já viu essas curvas que estão na figura a seguir??
A curva verde, talvez, seja a mais familiar, pois já vimos ela no colégio, é uma parábola (lembra das equações de segundo grau?). As outras já são um pouco diferentes!! A curva azul chamamos de elipse e as duas curvas em vermelho formam o que chamamos de uma hipérbole.
Essas figuras são chamadas de cônicas. São curvas definidas por certas equações predeterminadas e que são desenhadas no plano, ou seja, em 2D.
Bora começar pela parábola, que para alguns já é uma velha conhecida!!
O que é uma Parábola?
Ok, você deve se lembrar das aulas de matemática do ensino médio, que a parábola representa um gráfico das equações de segundo grau né? Pois é! Esse é o momento que peço pra você esquecer dessa definição e tentar enxergar a parábola com outros olhos, rs!
Vamos estudar a definição geométrica de parábola:
“Dado uma reta d e um ponto F, a parábola é o lugar geométrico dos pontos cuja a distância até F é igual a distância até a reta d.”
Relaxa que já já você vai entender!
Vamos lá, a definição fala de uma reta e um ponto né? Vamos começar daí:
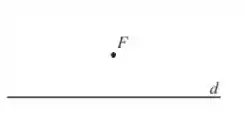
Observe agora essa imagem:
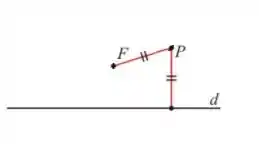
Notou que escolhendo esse ponto a distância entre o ponto e a retaé igual a distância entre ele e o ponto ? Esse ponto vai pertencer a parábola!
Para encontrá-la agora precisamos descobrir todos os pontos com essa propriedade:
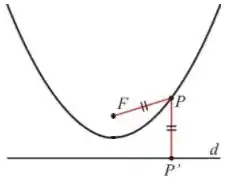
Prontinho já achamos a tão famosa parábola, o lugar geométrico dos pontos cuja a distância até F é igual a distância até a reta d. Fez mais sentido agora né?
Elementos da Parábola
Para construir e estudar a parábola, vamos precisar de alguns nomes. Observe a figura:
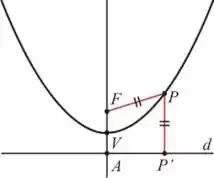
Temos que:
- Foco é o ponto
- Reta Diretriz, reta
- Eixo é a reta que contém o foco e é perpendicular a reta diretriz
- Vértice que é o ponto o qual é a interseção da parábola com o seu eixo, equidistante ao foco e à reta diretriz.
- , ou seja, o vértice é equidistante ao foco e à reta diretriz
- O Parâmetro de uma parábola é a distância entre o foco e a diretriz
Depois que traçou essa reta perpendicular a diretriz, nós obtemos mais umas relaçoes importantes:
Tipos de Parábolas
A parábola pode estar desenhada de 3 maneiras diferentes:
Caso 1 - Vértice da parábola é a origem e o seu eixo é o eixo dos
Caso 2 - Vértice da parábola é a origem e o seu eixo é o eixo dos
Caso 3 – Translação
Show de bola?! Não se assuste pequeno gafanhoto, pois vamos estudar cada um dos casos!
Caso 1
Trata-se de uma parábola com o vértice sendo a origem e o seu eixo é o eixo dos . Vamos pensar num exemplo:
Observe a expressão .
Atribuindo valores para e encontrando , temos a tabela:
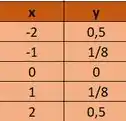
Colocando esses pontos no plano e ligando eles, temos isso aqui
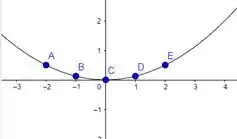
Obtemos o que queríamos , uma parábola com o vértice sendo a origem e o seu eixo é o eixo dos . Vamos generalizar agora:
Bem, seja um ponto com coordenadas um ponto qualquer da parábola de foco temos algo desse tipo:
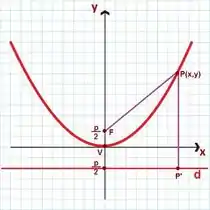
Essa parábola ta do mesmo jeitão da que vimos no exemplo ali em cima né? Hehe
Da definição de parábola, temos que:
Então nesse caso temos que:
Sendo pertencente à reta diretriz, temos que enquanto. Substituindo e calculando a distância da expressão temos:
=
Resolvendo essa equação chegamos em:
Essa é a forma padrão da equação da parábola de vértice na origem e eixo no eixo .
Então lá no nosso exemplo, em que , temos , ou seja, ali temos que
Como é sempre um valor positivo, os valores de e têm duas possibilidades:
Com essas duas possibilidade surgem as parábolas que conhecemos lá no fundamental!! Assim, na figura a seguir estão as duas possibilidades para e bem como suas retas diretrizes!!
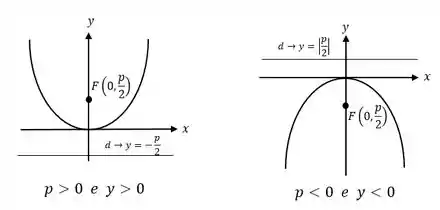
Esse foi nosso primeiro caso!! Vamos para o segundo caso!!
Caso 2
Vamos supor que ao invés de , tivéssemos . Fazendo o mesmo esquema que fizemos ali em cima, nossa parábola ficaria assim:
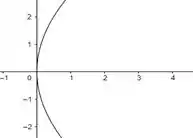
Eita! Como assim agora ela ta deitada?? Vamos analisar esse caso com essa figura genérica:
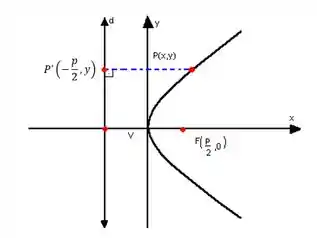
O passo a passo para determinar a equação da parábola é o mesmo do caso anterior, mas agora nosso foco é , nosso , fazendo o cálculo da distância, chegamos na expressão:
=
Essa é a equação da parábola quando o vértice é e o eixo é o eixo . Para esse caso novamente temos duas possibilidades para e , mostradas na figura:
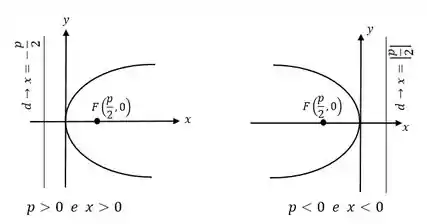
No nosso exemplo, , então e a nossa diretriz é .
Caso 3
Agora vamos supor a equação . Opa, repara que nesse caso ela ta “flutuando”, não ta colada em nenhum eixo:
Para entendermos bem esse caso, vamos começar falando de translação!! Translação nada mais é que uma mudança de coordenadas, como mostra a figura a seguir:
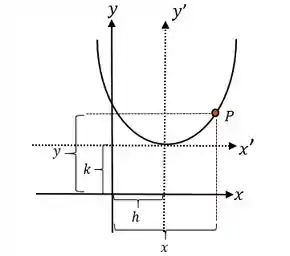
Na figura temos o sistema que é nosso velho conhecido, mas também temos em linhas tracejadas o sistema que foi criado para facilitar nossa vida. Então, olhando para a figura vemos que:
Reescrevendo:
Então no nosso exemplo:
Para resolver, vamos supor que e que , então teremos:
Com essa mudança de coordenadas caímos novamente no caso 1 ou 2.
Nesse caso, já vimos no caso 1 que , , . Mas, agora tudo isso está no sistema , agora vamos passar novamente pra , lembrando que e :
Então basicamente a coisa aqui é mudar as coordenadas, achar os parâmetros em e depois mudar de coordenada de novo beleza??
Essas ideias ficarão ainda mais claras nos exercícios!! Então vamos lá!! :D
Elementos da Parábola
Tipos de Parábolas
Caso 1
Caso 2
Caso 3
Exercícios Resolvidos
Exercício Resolvido #1
UFF, Lista 4 – Exercícios Geometria Analítica e Cálculo Vetorial, página 2, exercício 11
Encontrar as coordenadas do vértice, o foco e a equação da diretriz de cada uma das seguintes parábolas:
Passo 1
Opa!! Nosso problema envolve as parábolas!! Então, vamos colocar em prática tudo o que vimos sobre parábolas!! O enunciado pede para encontrarmos as coordenadas do vértice, o foco e a equação diretriz de cada uma das parábolas. Então, bora começar!!
Passo 2
a)
Essa expressão tem o jeito parecido de uma das equações que vimos na teoria, que é a seguinte:
Vimos também que essa equação é a equação de uma parábola que possui vértice na origem e seu eixo é o eixo . Bom, já temos o vértice e o eixo só de lembrar da teoria. Também sabemos, que com essas características o foco é . Mas, quem é ?
Para achar devemos comparar
Comparando, temos:
Então,
E nossa, diretriz?
A diretriz está sempre a uma distância do vértice, como nosso foco está na parte positiva,então isso indica que nossa diretriz estará na parte negativa:
Portanto, nossa diretriz é:
Pronto!! Nossa primeira parábola já está definida:
Passo 3
b)
Essa equação não se parece nem com o caso 1 e nem com o caso 2, mas com o caso 3, que possui translação!! É isso mesmo!!
Como vimos, para resolver esse tipo de exercício primeiro passamos a equação para um sistema genérico , resolvemos tudo para esse sistema e depois passamos para o sistema cartesiano novamente.
Então, nosso sistema genérico será:
Fazendo essas mudanças, teremos:
Vamos resolver, normalmente! Então primeiro, vamos encontrar o valor de :
Comparando:
Nosso foco no sistema será:
O vértice no sistema é .
Como temos que nosso foco está na parte negativa, então nossa reta diretriz estará na parte positiva e será . Logo,
Sempre lembre que o foco e a diretriz são simétricos em relação a algum dos eixos.
Bom, chegamos em todos os resultados, mas os resultados está no sistema , então chegou a hora de usarmos as relações,
Para passarmos do para .
Assim, para o sistema temos:
Substituindo as relações e ,temos:
Nossa parábola nos eixos possuem os seguintes elementos:
Passo 4
c)
Esse item é parecido com o anterior, o que vai alterar são as relações de e .
Então, primeiro escrevendo essas relações, temos:
Assim, teremos a expressão em :
Vamos tratar esse problema normalmente só que a diferença é que estamos num sistema de coordenadas , mas isso resolvemos depois ;).
Pelo jeito da expressão sabemos que o eixo da nossa parábola é o eixo e que o vértice no sistema é . Vamos encontrar o valor de para acharmos o foco e a diretriz!!
Comparando, temos:
Nosso foco no sistema é ,portanto:
Como nosso foco está no lado positivo, nossa diretriz estará no negativo, então:
Pronto! O problema terminou!! Nada disso!! Cuidado, achamos os resultados para o sistema genérico , mas as respostas sempre devemos dar em coordenadas cartesianas . Então, para terminar vamos usar as relações:
Substituindo, temos:
Agora, sim!! Nossas respostas são:,
Passo 5
d)
Nesse item não temos mais translação, mas note que agora quem está elevado ao quadrado éo e não mais o como estávamos fazendo. Então, agora, estamos no 1º caso da teoria.
Se estamos no 1º caso da teoria sabemos que o vértice é e que o eixo da parábola será, agora, o eixo dos . Falta, então, calcularmos o valor de para então descobrirmos as coordenadas do foco e a reta diretriz.
Então, comparando:
Nosso foco nesse caso é como vimos na teoria. Achamos que , substituindo temos:
Como nosso foco é negativo, a diretriz estará na parte positiva como mostra a figura:
Calculando será:
Pronto!! Como não tivemos que fazernenhuma mudança de coordenadas todos os nossos resultados já estão nas coordenadas . Então, temos como resultado: e .
Passo 6
e)
Nosso problema agora é parecido com o do item anterior, mas com translação, ou seja, teremos que fazer uma mudança de coordenadas. Para isso, vamos excrever as relações:
Substituindo essas relações obtemos a seguinte expressão no sistema :
Agora, estamos no caso do item anterior, mas num sistema transladado. Vamos calcularos parâmetros normalmente e depois fazemos a mudança de coordenadas. Pelo jeitão da expressão estamos no primeiro caso, ou seja, e nosso eixo é o eixo . Lembrando, como fizemos uma mudança de variável trabalharemos com o sistema . Podemos comparar então:
Da teoria sabemos, que , então nosso foco no sistema fica:
E nossa diretriz, também no sistema é . Como nosso foco está na parte negativa, nossoa diretriz estará na parte positiva, então:
Já que achamos tudo o que precisávamos no sistema , agora sim, podemos passar para o sistema . Para isso vamos utilizar as relações:
Substituindo, teremos:
Terminamos!! A solução desse item é: , e .
Resposta
,
e
, e
Exercício Resolvido #2
UFF, Lista 4 – Exercícios Geometria Analítica e Cálculo Vetorial, página 4, exercício 27
Achar a equação da parábola que passa pelos pontos , e
Passo 1
Nossa! Não sei nem por onde começar!!
Calma!! Tem um detalhe que ainda não falamos que vai te ajudar muito!!
O detalhe é o seguinte:
- Se a reta diretriz for paralela ao eixo então a equação é
- Se a reta diretriz for paralela ao eixo então a equação é
Passo 2
Então, para acharmos a expressão precisamos identificar à qual eixo a parábola é paralela. Para isso, vamos marcar os pontos no plano e ver qual o jeitão da parábola. Fazendo um esboço bem rápido, temos:
Pela figura nossa parábola possui diretriz paralela ao eixo , então, nossa equação é:
Passo 3
Sabendo disso precisamos substituir os pontos na equação. Substituindo, teremos:
Para
Para
Como
Para
Como ,
Com as expressões e conseguimos achar os valores de e . Resolvendo o sistema a seguir, temos:
Isolando na primeira equação, temos:
Substituindo na segunda equação:
Então,
Chegamos nos valores:
Assim, sabendo que a expressão é , a expressão da nossa parábola fica:
Resposta
Exercício Resolvido #3
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 217-4.
Determinar a equação da parábola de foco em , sendo a equação da diretriz.
Passo 1
Temos um exerc´ício muito parecido com o anterior!! Mas, agora, não temos mais o vértice, mas o foco. Assim, com o foco e a diretriz devemos determinar a equação da parábola.
Bora começar, então?
Passo 2
Primeiro, devemos ver em qual dos três casos estamos!! Como nenhuma das coordenadas de é zero, isso nos indica que estamos no caso , ou seja, translação. Temos, também outra dica importante!! Como sabemos que a reta diretriz é , então, nossa equação da parábola tem o seguinte formato:
Sempre que tivermos dados como esses é bom fazer um esboço para clarear nosso problema!!
Passo 3
Esboçando, temos:
Da figura conseguimos tirar uma primeira informaçãosobre . Devido a concavidade a parábola estar apontando para o lado negativo, isso indica que estamos no caso onde . Assim,
Da figura também conseguimos ver que o vértice da parábola é o ponto médio entre e , logo a coordenada do vértie vale , e a coordenada é a mesma do foco. Assim, temos:
Lá na teoria vimos que quando temos tranlação temos as seguintes relações:
Assim, se temos o vértice em e no sistema temos , temos as relações:
Pronto!! Temos tudo o que precisávamos para completar nossa expressão . Assim, se e :
Chegamos na expressão da nossa parábola!!
Resposta
Exercício Resolvido #4
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 216-3.
Determinar a equação da parábola de vértice , sabendo que é a equação de sua diretriz.
Passo 1
O problema nos dá o vértice e a equação da reta diretriz da parábola, e nós com esses dados devemos determinar a equação desta parábola. Mas, como farei isso, não vimos nada assim!!
Calma!! Vamos por partes!!
Passo 2
Analisando o vértice sabemos que não estamos nem no caso 1 e nem no caso 2, porque nesses dois casos o e temos que . Assim, estamos no caso de uma translação. Além disso, sabemos que a reta diretriz é , isso nos indica que a nossa parábola é da seguinte maneira:
Assim, sabemos que a forma geral da nossa parábola, será:
Passo 3
Para determinar nossa parábola, precisamos então determinar os valoresde e . Para isso, vamos fazer o inverso do que vínhamos fazendo, ou seja, sabemos que no sistema o vértice é e sabemos que no vale .
Assim, teremos:
Substituindo em :
Substituindo em :
Portanto, chegamos na seguinte expressão:
Mas, e quanto vale?
Para achar fica mais fácil fazermos um esboço da parábola.
Passo 4
Fazendo um esboço obtemos a seguinte figura:
Pela figura temos que:
Que é a distância do nosso vértice em verde pra reta diretriz em azul!
Então !
Eu sei que deve ser um valor negativo, pois a parábola está nos !
Assim, já que achamos o valor de , falta colocar na expressão:
Substituindo:
Prontinho, chegamos na nossa resposta!!