1. Em cada parte, encontre a equação característica da matriz simétrica dada e depois, por inspeção, determine as dimensões dos autoespaços
(a) (b)
(c) (d)
(e) (f)
Passo 1
(f) Para achar a equação característica fazermos:
Onde:
Passo 2
Primeiro vamos fazer:
Passo 3
Retornando para:
Substituindo os valores:
Reescrevendo:
Então, temos:
Calculando o determinante, lembrando que para uma matriz , utilizamos o Teorema de Laplace, onde primeiro escolhemos e fila (linha ou coluna– preferencialmente com maior número de zeros) onde o determinante será a soma entre cada elemento multiplicado pelo seu cofator.
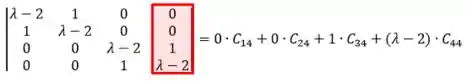
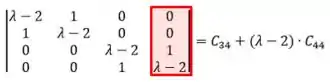
Vamos calcular os cofatores:
Onde é a matriz resultante da exclusão da linha e coluna :
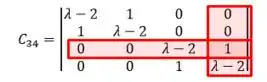
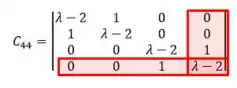
Calculando o novo determinante, lembrando que para uma matriz , primeiro repetimos as duas primeiras colunas multiplicamos os elementos da diagonal principal e suas paralelas, e subtraímos do resultado da multiplicação dos elementos da diagonal secundária e suas parelas.
Reorganizando:
Passo 4
Retornando para:
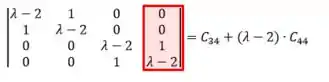
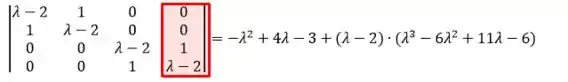
Reorganizando:
Relembrando:
Logo:
Passo 5
Determinando os autoespaços:
Utilizando um software, temos: