Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios de Diagonalização - Lista de Exercícios Resolvida

Ver Teoria

Questão 1

Diga se a matriz abaixo é diagonalizável:

2 1 0 1

Ver solução completa

Questão 2

Seja T : R 3 ⟶ R 3 dada por:

T x , y , z = ( x + 2 y ,   - 2 x + y ,   3 z )

a   Encontre os autovalores de T e os respectivos autoespaços.

b   A transformação T é diagonalizável? Se sim, dê sua forma diagonal.

Ver solução completa

Questão 3

A matriz abaixo está fatorada na forma M D M - 1 . Sem fazer contas, determine os autovalores da matriz e bases para cada um dos autoespaços.

3 1 - 2 - 2 0 4 0 0 2 = 1 2 - 1 1 0 2 1 1 0 2 0 0 0 2 0 0 0 1 - 2 - 1 4 2 1 - 3 1 1 - 2

Ver solução completa

Questão 4

Considere A x , y , z = x + y 2 , x + y 2 ,   z . Determine P e Q tais que:

a   P - 1 A P = 1 0 0 0 1 0 0 0 0

b   Q - 1 A Q = 1 0 0 0 0 0 0 0 1

Ver solução completa

Questão 5

Sejam T : R 3 → R ³ o operador linear cuja matriz relativamente à base canônica de R 3 é a b c 0 a d 0 0 e , em que a , b , c , d , e são números reais que satisfazem a ≠ e . Então

a) T é diagonalizável se e = 0

b) T é diagonalizável se c = 0

c) T é diagonalizável se b = 0

d) T não é diagonalizável

e) T é diagonalizável se d = 0

Ver solução completa

Questão 6

Sejam A 1 e A 2 ∈   M 5 ( R ) e considere as seguintes afirmações:

  1. Se A 1 e A 2 são semelhantes, então qualquer autovalor de A 1 é autovalor de A 2
  2. Se T 1 : R 5 → R 5 e T 2 : R 5 → R 5 são operadores lineares β uma base de R 5 , [ T 1 ] β   =   A 1 e [ T 2 ] β   =   A 2 e se A 1 e A 2 são semelhantes então todo autovetor de T 1 também é autovetor de T 2 .
  3. Se A 1 e A 2 possuem os mesmos autovalores com as mesmas multiplicidades algébricas, então A 1 e A 2 são semelhantes.

Ver solução completa

Questão 7

Seja T :     R 5 → R 5 um operador linear cujos polinômios característicos é p t = - t 3 ( t + 1 ) ( t - 3 ) . Denote o operador identidade de R 5 por I. Qual das seguintes afirmações é falsa?

a   S e   T   é   d i a g o n a l i z á v e l ,   e n t ã o dim ⁡ I m T + dim ⁡ I m T + I + dim ⁡ I m T - 3 I = 5 .

b   V a l e dim ⁡ K e r T + I = 1 .

c   S e dim ⁡ I m T = 3 ,   e n t ã o   T   n ã o   é   d i a g o n a l i z á v e l .

d   V a l e dim ⁡ K e r T + dim ⁡ K e r T + I + dim ⁡ K e r T - 3 I ≤ 5

e   S e   v ∈ R 5   é   t a l   q u e   T v = 2 v ,   e n t ã o   v   é   o   v e t o r   n u l o .

Ver solução completa

Questão 8

Seja n um inteiro positivo, e considere as seguintes afirmações sobre o operador linear T : P n R → P n ( R ) definido por T ( p x = x p ' ( x ) , para todo p x ∈ P n ( R ) , em que p ' ( x ) denota a derivada de p ( x ) .

I .   O   o p e r a d o r   T   é   d i a g o n a l i z á v e l .

I I .   A   s o m a   d o s   a u t o v a l o r e s   d e   T   é   n n + 1 2

I I I .   O   o p e r a d o r   T   é   i n v e r s í v e l .

Está correto o que se afirma em

a   I   e   I I ,   a p e n a s

b   I I   e   I I I ,   a p e n a s

c   I   e   I I I ,   a p e n a s

d   I I ,   a p e n a s

e   I , I I   e   I I I .

Ver solução completa

Questão 9

Seja n   um interno maior do que 1 e seja A ∈ M n ( R ) . Suponha que A seja diagonalizável e que todos os seus autovalores tenham valor absoluto menos do que 1. Considere as seguintes afirmações:

I .   - 1 < det ⁡ A < 1 .

I I .   T o d o s   o s   a u t o v a l o r e s   d e   A   t ê m   m u l t i p l i c i d a d e   g e o m é t r i c a   n e c e s s a r i a m e n t e   i g u a l   a   1

I I I .     A   m a t r i z   A - I n   é   i n v e r t í v e l .

Ver solução completa

Questão 10

Considere as seguintes afirmações sobre uma matriz A   ∈ M 3 R de polinômio característico p t = - t 3 + 4 t 2 - 5 t + 2 .

I .   A   é   i n v e r t í v e l ;

I I .   A   é   n e c e s s a r i a m e n t e   d i a g o n a l i z á v e l ;

I I I .   - 2   é   u m   a u t o v a l o r   d e   A

Está correto o que se afirma em:

a   I   a p e n a s ,             b   I , I I   e   I I I ,           c   I   e   I I I   a p e n a s ,           d   I I   a p e n a s ,     e   I I   e   I I I   a p e n a s

Ver solução completa

Questão 11

Sejam α , β ∈ R . Sobre a matriz A =   1 1 α 0 0 β 0 0 1 , está correto afirmar que ela

a   é   d i a g o n a l i z á v e l   s e ,   e   s o m e n t e   s e ,   α = - β

b   é   d i a g o n a l i z á v e l   s e ,   e   s o m e n t e   s e ,   α = β

c   é   d i a g o n a l i z á v e l ,   q u a i s q u e r   q u e   s e j a m   α   e   β

d   é   d i a g o n a l i z á v e l   s e ,   e   s o m e n t e   s e ,   α = β = 0

e   n ã o   é   d i a g o n a l i z á v e l ,   q u a i s q u e r   q u e   s e j a m   α   e   β

Ver solução completa

Questão 12

Considere que a matriz abaixo é de uma transformação linear T : R 3 ⟶ R 3 e que α é a base canônica de R 3 :

T β α = 1 - 2 0 2 m 2 0 2 1

  1. Determine o polinômio característico de T .
  2. Para que valor(es) de m   a transformação T tem apenas um autovalor λ ? Determine o autoespaço V λ ;
  3. T   é diagonalizável para algum valor de m ?

Ver solução completa

Questão 13

Sejam 𝐴   ∈   𝑀 6 𝑅 uma matriz real e 𝑇 : 𝑅 6 → 𝑅 6 o operador linear tal que 𝑇 𝑐 𝑎 𝑛 = 𝐴 , em que 𝑐 𝑎 𝑛   denota a base canônica de 𝑅 6 . Se o polinômio característico de 𝑇   for:

𝑝 𝑇 𝑡   =   𝑡 2   +   𝑡   +   1 𝑡 − 2 2 𝑡 + 1 𝑡

então poderemos afirmar que:

(a) 𝐴   será diagonalizável sobre R, mas não será diagonalizável sobre C

(b) 𝐴   não será diagonalizável sobre C e 𝐴   será diagonalizável sobre R se, e somente se, existirem vetores linearmente independentes 𝑣   e   𝑤 em 𝑅 6 tais que 𝑇 𝑣 =   2 𝑣   𝑒   𝑇 𝑤 =   2 𝑤

(c) 𝐴   não será diagonalizável nem sobre R, nem sobre C

(d) 𝐴   não será diagonalizável sobre R e 𝐴   será diagonalizável sobre C se, e somente se, existirem vetores linearmente independentes 𝑣   e   𝑤 em 𝑅 6 tais que 𝑇 𝑣 =   2 𝑣   𝑒   𝑇 𝑤 =   2 𝑤

(e) 𝐴   será diagonalizável sobre C, mas não será diagonalizável sobre R.

Ver solução completa

Questão 14

06) Seja n um inteiro maior do que 1 . Considere as seguintes afirmações sobre uma matriz A ∈ M n ( R ) .

I . Se A diagonalizável sobre C , então A é também diagonalizável sobre R .

I I . Seja L o operador linear do espaço vetorial complexo C n tal que L c a n = A . Se λ ∈ C é autovalor de L , então d i m ⁡ ( K e r L - λ I ) = dim ⁡ K e r L -   λ - I .

I I I .   Seja T o operador linear do espaço vetorial real R n tal que T c a n = A .   Se A é diagonal e C uma base ortonormal de R n em relação ao produto interno usual, então T C é diagonal.

Está correto o que se afirma em:

A) I I , apenas.

B) I I I , apenas.

C) I e I I , apenas.

D) I e I I I , apenas.

E) I ,   I I e I I I apenas.

Ver solução completa

Questão 15

Seja A uma reflexão do R 3 através do eixo X seguida da expansão de um fator 11 na direção do eixo Y . Os autovalores de A são:

( a ) 0 ,   1 e - 11

( b ) 1 ,   - 1   e 11

( c ) 1 ,   - 1 e - 11

( d ) 0 ,   1   e 11

Ver solução completa

Questão 16

Seja T : R 2 ⟶ R 2 uma transformação linear tal que T - 1,1 = 5 ( - 1,1 ) e T 1,2 = 1 5 1,2 . Seja A matriz de T   na base canônica. Calcule a soma dos elementos da primeira linha de A .

(a) 9 5

(b) - 5 3

(c) 0

(d)   1 5

Ver solução completa

Questão 17

Dizemos que duas matrizes A , B ∈ M 2 × 2 ( R ) comutam se satisfazem A B = B A . Considere o conjunto C ( A ) de todas as matrizes que comutam com A

C A = B ∈ M 2 × 2 R A B = B A }

Considere agora o caso particular das matrizes A = 1 - 1 - 4 1 e D = 3 0 0 - 1 .

( c ) Mostre que existe uma matriz P invertível tal que A = P D P - 1 .

(Observação: é possível mas não é necessário calcular a matriz P , nem P - 1 .)

( d ) Mostre que se uma matriz B comuta com D , então B é diagonal.

Ver solução completa

Questão 18

Seja T : R 3 → R 3 uma transformação linear dada por:

T x , y , z = ( x + 3 y - 4 z , y , 2 y - 3 z )

(a) Calcular os autovalores de T.

(b) Calcular os autovetores de T.

(c) T é diagonalizável? Justificar. Em caso afirmativo, encontre uma base na qual a matriz de T é uma matriz diagonal D. E exiba D.

Ver solução completa

Questão 19

Seja T : U ⟶ U uma transformação linear. Usaremos as notações T 2 = T ∘ T e T 3 = T ∘ T ∘ para denotar composições de T . Suponha que:

  1. T 3 v = 0 para todo v ∈ U ,
  2. Existe v 0 ∈ U tal que T 2 v 0 ≠ 0

Chamamos esse tipo de transformação de nilpotente de ordem 3 .

b   Mostre que 0 é o único autovalor de T

(Dica: comece com um autovetor de T .)

c   Mostre que T não é diagonalizável .

(Dica: como seria a matriz de T se fosse diagonalizável?)

Ver solução completa

Questão 20

Seja T : R 3 ⟶ R 3 a reflexão (espelhamento) em relação ao plano π e

T γ = - 1 0 - 2 2 1 2 0 0 1

A matriz de T na base γ = { v 1 ,   v 2 , v 3 } de R 3 .

( c ) Sabendo que δ = { u 1 , u 2 , u 3 } é uma base de R 3 cujos elementos são autovetores de T , sendo u 1 e u 2 associados ao mesmo autovalor, encontre T δ .

( d ) Dê um exemplo de um subespaço vetorial H de R 3 tal que as duas seguintes condições sejam satisfeitas:

  • H não é autoespaço de T , mas é invariante por T
  • dim ⁡ H = 2

Ver solução completa

Questão 21

Considere a função D : P 3 ⟶ P 3 definida por:

D a + b x + c x 2 + d x 3 = b + 2 c x + 3 d x 2

(Observe que D é a transformação que deriva o polinômio)

( d ) D é diagonalizável? Justifique:

Ver solução completa

Questão 22

Seja T : R 3 → R 3 um operador linear tal que:

M - 1 T c a n M = 1 0 0 0 2 0 0 0 3

Em que

M = 1 0 1 0 1 1 1 1 0

E can denota a base canônica de R 3 . Temos que T ( 5,3 , 4 ) é igual a:

  1. 9,8 , 5 ;
  2. 7,7 , 6 ;
  3. 8,5 , 9 ;
  4. 5,11,13 ;
  5. 10,6 , 8 .

Ver solução completa

Questão 23

Considere as seguintes afirmações:

  1. Se n for um inteiro positivo, T : R n → R 988 for uma transformação linear sobrejetora, B for uma base de R n e C for uma base de R 988 , então as colunas da matriz T B C serão linearmente independentes;
  2. Se B = { e 1 ,   e 2 ,   … ,   e 988 } for uma base de R 988 e T : R 988 → R 988 for a transformação linear tal que T e 1 = e 2 e T e j = 0 para todo j = 2 , … ,   988 ,   então T B 2 = 0 ;
  3. Se T : R 988 → R 988 for uma transformação linear diagonalizável, então a matriz que representa T na base canônica terá determinante não nulo.

Assinale a alternativa correta:

  1. Apenas a afirmação (II) é verdadeira;
  2. Apenas as afirmações (I) e (II) são verdadeiras;
  3. Apenas as afirmações (I) e (III) são verdadeiras;
  4. Todas as afirmações são falsas;
  5. Todas as afirmações são verdadeiras;

Ver solução completa

Questão 24

Sejam T : R 3 → R 3 o operador linear cuja matriz relativamente à base canônica de R 3 é a b c 0 a d 0 0 e , em que a , b , c , d , e são números reais que satisfazem a ≠ e . Então,

Escolha uma opção:

  1. T é diagonalizável se e = 0 ;
  2. T é diagonalizável se c = 0 ;
  3. T é diagonalizável se b = 0 ;
  4. T não é diagonalizável;
  5. T é diagonalizável se d = 0 ;

Ver solução completa

Questão 25

Sejam a ∈ R , V um espaço vetorial de dimensão 5 e T   : V → V um operador linear cujo polinômio característico seja:

p T t = - ( t 3 - a t ) ( t 2 - 4 )

Pode-se afirmar que:

  1. Se a < 0 , então T não será diagonalizável;
  2. Se a = 4 , então T será diagonalizável;
  3. T é injetor;
  4. dim ⁡ K e r T ≥ 2 ;
  5. Se a ≥ 4 , então T será diagonalizável.

Ver solução completa

Questão 26

Seja T : R 3 → R 3 uma transformação linear e suponha que 1,3 , 5 ,   ( 2 ,   - 3 ,   7 ) e ( 5 ,   9 ,   3 ) sejam autovetores de T correspondentes respectivamente aos autovalores 2 , 1 e 9 . Temos que o determinante da matriz que representa T com respeito à base canônica de R 3 é igual a:

Escolha uma opção:

  1. 18
  2. 40
  3. 36
  4. 15
  5. 20

Ver solução completa

Questão 27

Se A 11 ,   3 = ( - 11 ,   - 3 )   e A 7 ,   2 = 7 ,   2 , assinale abaixo o vetor X → tal que A 2 X → = 2 ,   3

  1. 1 ,   3 .
  2. 3 ,   1 .
  3. 3 ,   2 .
  4. 2 ,   3 .

Ver solução completa

Questão 28

Sejam 2   e - 5 autovalores de A , uma matriz 3 × 3 . Qual, dentre as condições abaixo, NÃO garante que a matriz A é diagonalizável?

  1. A não possui inversa.
  2. A possui inversa.
  3. dim ⁡ n u c l e o A + 5 I = 2 .
  4. dim ⁡ n u c l e o A - 4 I = 1 .

Ver solução completa

Questão 29

Considere a transformação linear T : R 3 → R 3 cuja matriz na base canônica é

T ε = 3 1 0 0 2 1 - 3 - 3 - 1  

E cujo polinômio característico é

p λ = - λ λ - 2 2

  1. Determine se existe a matriz inversa de T ε . Em caso afirmativo determine essa matriz. Justifique claramente sua resposta.
  2. Determine se T ε é diagonalizável. Em caso afirmativo determine uma forma diagonal de T . Em caso negativo justifique claramente porque não é diagonalizável.

Ver solução completa

Questão 30

Decida se cada afirmação abaixo é verdadeira ou falsa. Se a afirmação for verdadeira, apresente uma demonstração. Se a afirmação for falsa, exiba explicitamente um contraexemplo.

(a.1) Se T :   R 3 → R 3 é uma transformação linear tal que seu polinômio característico é p λ = - λ 3 - 4 λ ,   então T é diagonalizável.

(a.2) Se T :   R 3 → R 3 uma transformação linear tal que seu polinômio característico é p λ = - λ 3 - 4 λ ,   então d i m ( I m ( T ) ) =   2 .

Ver solução completa

Questão 31

Seja T : R 3 → R 3 a transformação linear dada por T x , y , z = 2 x + z , 5 x - 3 y + z , - 3 z .

b T é diagonalizável? Se sim, encontre uma base β onde T β β é uma matriz diagonal.

Ver solução completa

Questão 32

Seja T : R 3 → R 3 um operador linear que tem 2 e 3 como autovalores e tal que os autoespaços correspondentes são V 2 = x , y , z : x + y + z = 0 e V 3 = x , x , - x : x ∈ R .

a T é diagonalizável? Em caso afirmativo, encontre uma base de R 3 formada por autovetores de T . Justifique.

b Dado x , y , z ∈ R 3 , determine T x , y , z

Ver solução completa

Questão 33

Considere as seguintes afirmações:

I Se todos os autovalores de uma matriz são distintos, então a matriz é diagonalizável.

I I Seja A uma matriz 4 × 4 não diagonalizável, então A possui 4 autovetores linearmente independentes.

Qual das opções abaixo é CORRETA?

a   A afirmativa I é verdadeira e I I é verdadeira.

b   A afirmativa I é falsa e I I é falsa.

c   A afirmativa I é verdadeira e I I é falsa.

d   A afirmativa I é falsa e I I é verdadeira.

Ver solução completa

Questão 34

Considere a reflexão R : R 3 → R 3   com relação à reta r   =   { t ( 3 ,   1 ,   1 ) | t   ∈ R } .

(a) Determine os autovalores de R   e os respectivos autoespaços.

(b) Determine a matriz canônica de R , ou seja, a matriz R ε onde ε = { ( 1 ,   0 ,   0 ) , ( 0 ,   1 ,   0 ) , ( 0 ,   0 ,   1 ) } .

(c) Determine N u c ( R ) e I m ( R ) .

(d) Diagonalize ortogonalmente R ε , ou seja, encontre uma matriz D diagonal, uma matriz P ortogonal e sua inversa tais que R ε   = P D P - 1 .

(e) Calcule R ε 20 e R ε 21 .

Ver solução completa

Questão 35

Sejam n   ≥   1   um inteiro e A   ∈   M n ( R ) . Considere as seguintes afirmações:

1- se a matriz A   for diagonalizável, então a transposta da matriz A também será diagonalizável;

2- se o polinômio caracterıstico de A tiver n raízes reais distintas, então a matriz A será diagonalizável;

3- se a matriz A for inversível é diagonalizável, então a matriz A - 1 também será diagonalizável.

Assinale a alternativa correta:

  1. apenas as afirmações (I) e (II) são necessariamente verdadeiras;
  2. apenas as afirmações (II) e (III) são necessariamente verdadeiras;
  3. apenas a afirmação (II) é necessariamente verdadeira;
  4. todas as afirmações são necessariamente verdadeiras;
  5. apenas as afirmações (I) e (III) são necessariamente verdadeiras.

Ver solução completa

Questão 36

Seja fixado um sistema de coordenadas Σ   =   ( O ,   B ) no plano, com B

uma base ortonormal. Denote por A o conjunto formado pelos números

reais a para os quais a equação

x 2   -   2 a x y   +   5 y 2   =   10

representa uma elipse. Assinale a alternativa correta:

  1. A   = { a   ∈   R   :   | a |   < √ 5 } ;
  2. A   = { a   ∈   R   :   a > 20 } ;
  3. A = R
  4. A = { }
  5. A = { a   ∈   R   : a = 0   o u     | a | > √ 5 } ;

Ver solução completa

Questão 37

Seja T : R 3 → R 3 um operador linear tal que

K e r ( T ) = [ 1,0 , - 1 ] ; K e r ( T - 2 I ) = [ 1,0 , 1 ] ; K e r ( T - I ) = [ 0,1 , 1 ]

Seja A a matriz que representa T na base canônica de R 3 . E seja D a matriz

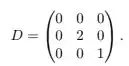
Considere as seguintes matrizes inversíveis

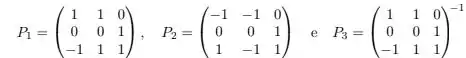
Dentre P 1 ,   P 2   e   P 3 , as matrizes P tais que A   =   P   D P - 1 são:

  1. P 2   e   P 3
  2. P 2
  3. P 1
  4. P 1   e   P 2
  5. P 3

Ver solução completa

Questão 38

Sejam n um inteiro positivo, V um espaço vetorial complexo de dimens ao n , T   :   V   →   V um operador linear e S   :   V   →   V o operador linear definido por

S   =   T   ◦   T   +   I

Assinale a alternativa contendo uma afirmação que NÃO é necessariamente verdadeira:

(a) T   ◦   S   =   S   ◦   T ;

(b) se S for o operador nulo, então T será bijetor;

(c) se λ   ∈   C for um autovalor de T , então λ 2   +   1 será um autovalor de S ;

(d) se T for diagonalizável, então S será bijetor;

(e) se o polinômio característico de T tiver n raízes reais distintas, então S

será bijetor.

Ver solução completa

Questão 39

Considere o espaço vetorial R 2 munido do seu produto interno usual. Seja T   :   R 2   →   R 2 a transformação linear tal que

em que B é a base de R 2 dada por:

B   =   { ( 1 ,   2 ) , ( 1 ,   1 ) } .

Considere as seguintes afirmações:

(I) T é simétrico;

(II) T possui dois autovalores distintos;

(III) T ́ é diagonalizável.

Assinale a alternativa correta:

Assinale a alternativa correta:

(a) todas afirmações são necessariamente verdadeiras;

(b) apenas as afirmações (I) e (III) são necessariamente verdadeiras;

(c) apenas as afirmações (I) e (II) são necessariamente verdadeiras;

(d) apenas as afirmações (II) e (III) são necessariamente verdadeiras

(e) Todas as afirmações são falsas.

Ver solução completa

Questão 40

Seja A uma matriz 2 × 2   com autovalores 6   e 7 associados, respectivamente, aos autovetores ( 1 ,   1 ) e - 1,1 . Assinale a soma dos elementos da primeira coluna de A :

(a) - 1

(b) - 6

(c)   13

(d)   6

Ver solução completa

Questão 41

É dado que o conjunto dos autovalores da matriz A = - 3 2 2 2 1 - 2 - 4 2 3 é - 1,1 . Então:

(a) A não é diagonalizável

(b) A é uma reflexão ortogonal

(c) A é uma reflexão não ortogonal

(d) A é uma projeção

Ver solução completa

Questão 42

A matriz 2 × 2 que tem autovetores ( 1 , π ) e ( 2 , 2 ) associados, respectivamente, aos autovalores 2 e 3 é:

Ver solução completa

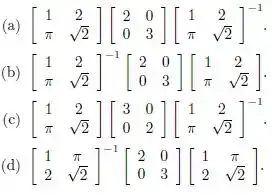
Questão 43

Considere a matriz

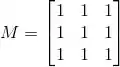
(a) Determine os autovalores de M.

(b) Determine uma base de autovetores de M.

(c) Diagonalize ortogonalmente M, ou seja, encontre matrizes P ortogonal e D diagonal tais que M = P D P T

Ver solução completa

Questão 44

Seja A uma matriz n × n . Considere as afirmações abaixo:

(I) Se as colunas de U formam uma base do R n composta por autovetores de A então existe D diagonal tal que A U = U D .

(II) As matrizes A e A T tem os mesmos autovalores.

(a) (I) é falsa e (II) é falsa.

(b) (I) é falsa e (II) é verdadeira.

(c) (I) é verdadeira e (II) é falsa.

(d) (I) é verdadeira e (II) é verdadeira.

Ver solução completa

Questão 45

Dada a matriz A = - 1 3 3 - 1 encontre uma matriz ortogonal P tal que P T A P é diagonal.

Ver solução completa

Questão 46

Seja T :   R 3 → R 3 uma transformação linear dada por:

T x , y , z = x - 3 z , y - 6 z , - 2 z

(a) Obtenha o polinômio característico e calcule os autovalores de T.

(b) Obtenha para cada um dos autovalores de T uma base para seu respectivo autoespaço (subespaço associado).

(c) T é diagonalizável? Justifique. Em caso afirmativo, determine uma base na qual a matriz de T é uma matriz diagonal e exiba tal matriz.

Ver solução completa

Questão 47

Sejam R : R 2 → R 2 a reflexão ortogonal através da reta y = x e S : R 2 → R 2 a reflexão ortogonal através da reta y = - x . Qual é o polinômio característico p λ de T = R S

a   p λ = λ 2

b   p λ = λ λ + 1

c   p λ = λ + 1 2

d   p λ = λ λ - 1

Ver solução completa

Questão 48

Considere as seguintes afirmações:

(I) se V     for um espaço vetorial complexo de dimensão finita, T : V → V   for um operador linear e λ   ∈   C   for um autovalor de T   , então o conjugado de λ   também será um autovalor de T   ;

(II) se uma matriz real A ∈ M n R for diagonalizável sobre C   , então ela também será diagonalizável sobre R  

(III) se uma matriz real A   ∈   M n R for diagonalizável sobre R   , então ela também será diagonalizável sobre C .  

Quais afirmações são verdadeiras?

  1. Apenas a afirmação (II) é verdadeira;

  2. Apenas a afirmação (III) é verdadeira;

  3. Apenas as afirmações (II) e (III) são verdadeiras;

  4. Apenas as afirmações (I) e (II) são verdadeiras;

  5. Apenas a afirmação (I) é verdadeira;

Ver solução completa

Questão 49

Sejam a , b   ∈ R . Sobre a matriz A =   a b 0 0 1 2 0 0 2 , é correto afirmar que

a   s e   A   é   d i a g o n a l i z á v e l   e   b ≠ 0 ,   e n t ã o   a ≠ 1   e   a ≠ 2

b   s e   b = 0 ,   e n t ã o   A   n ã o   é   d i a g o n a l i z á v e l .

c   A   é   s e m p r e   d i a g o n a l i z á v e l

d   s e   a = 2 ,   e n t ã o   A   n ã o   é   d i a g o n a l i z á v e l ,   q u a l q u e r   q u e   s e j a   b .

e   s e   a = 1 ,   e n t ã o   A   é   d i a g o n a l i z á v e l   q u a n d o   b = 1 .

Ver solução completa

Questão 50

Seja a ∈ R e considere a matriz:

A = a 0 0 3 2 0 6 2 a

Pode-se afirmar que:

  1. A será diagonalizável se, e somente se, a = 1 ;
  2. A será diagonalizável se, e somente se, a = 0 ;
  3. A será diagonalizável se, e somente se, a = 2 ;
  4. A não é diagonalizável;
  5. Se a ≠ 2 , então A será diagonalizável.

Ver solução completa

Questão 51

Considere a matriz A = 1 0 0 - 1 1 - 1 1 0 2 .

a Determine os autovalores de A .

b Para cada autovalor λ determine uma base para o autoespaço V λ correspondente (subespaço associado ao autovalor λ ).

c T é diagonalizável? Se sim, escreva uma base β do R 3 onde T é diagonalizável e determine a matriz T β β .

Ver solução completa

Questão 52

Considere a matriz A = 1 2 3 1 2 3 1 2 3 . Determine se A é diagonalizável, e caso seja ache a diagonalização de A .

Ver solução completa

Questão 53

Seja p A o polinômio característico da matriz A .

Assinale a alternativa FALSA:

( a ) As raízes de p A são iguais às raízes de p A T

( b ) Se todas as raízes de p A são iguais então A é diagonalizável

( c ) Se todas as raízes de p A são complexas então A não tem autovetores

( d ) Se todas as raízes de p A são iguais então A tem autovetor

Ver solução completa

Questão 54

Considere a transformação linear T :   R 3 → R 3 cuja matriz na base canônica α é dada por:

[ T ] α α = 1 0 2 0 1 1 0 0 2

a)Determine o polinômio característico e calcule os autovalores λ   de T .

b)Para cada autovalor λ de T determine o subespaço associado V λ .

c)   T é diagonalizável? Se sim, exiba uma base β de R 3 e [ T ] β β onde isso acontece.

Ver solução completa

Questão 55

Considere o espaço vetorial R 3 munido do seu produto interno usual e seja T   :   R 3   →   R 3 o operador linear tal que

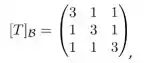
em que B denota a base

B   =   { ( 2,0 , 0 ) , ( 0,1 , 0 ) , ( 0,0 , 1 ) }

de   R 3 . Assinale a alternativa correta:

(a) T é diagonalizável e não é simétrico;

(b) T não é diagonalizável;

(c) T é simétrico;

(d) existe uma base ortonormal C de R 3 tal que a matriz [ T ] c é diagonal;

(e) T é diagonalizável e não é invertível.

Ver solução completa

Questão 56

Sejam V um espaco vetorial real de dimensão 13   e   T   :   V   →   V um operador

linear cujo polinômio característico seja:

p ( t )   =   - t 8 ( t   -   1 ) 3 ( t   -   2 ) 2 .

Assinale a alternativa contendo uma igualdade que NÃO implique que T seja diagonalizável:

  1. d i m ( k e r ( T ) ) + d i m ( k e r ( T - I ) ) - d i m ( i m g ( T - 2 I ) ) = 0
  2. d i m ( k e r ( T ) ) + k e r ( i m g ( T - I ) ) + d i m ( i m g ( T - 2 I ) ) = 24
  3. d i m ( i m g ( T ) ) + k e r ( i m g ( T - I ) ) + d i m ( i m g ( T - 2 I ) ) = 26
  4. d i m ( i m g ( T ) ) + k e r ( i m g ( T - I ) ) + d i m ( k e r T - 2 I ) ) = 13
  5. d i m ( k e r ( T ) ) + k e r ( k e r ( T - I ) ) + d i m ( k e r ( T - 2 I ) ) = 13

Ver solução completa

Questão 57

Q3. Seja k ∈ R e considere o operador linear T : R 3 → R 3 tal que

T c a n = 1 1 k 0 1 k 0 1 1

Em que can denota a base canônica de R 3 . Temos que T será diagonalizável se, e somente se:

a) k ≤ - 1 ;

b) k ∈   ] - 1,1 [ ;  

c) k ≥ 1 ;

d) k > 0 ;

e) k ≤ - 2 .

Ver solução completa

Questão 58

Verdadeiro ou Falso? Forneça uma justificativa para sua resposta.

( c ) A matriz A = 1 1 0 1 é diagonalizável.

Ver solução completa

Questão 59

A transformação linear T realiza a reflexão ortogonal dos vetores de R 3 pelo plano x + y - z = 0 , seguida da multiplicação por 3 . Então é FALSO afirmar que:

a   Dimensão do núcleo de T é igual a 0

b   T é diagonalizável

c   T é invertível

d   1 e - 1 são autovalores de T

Ver solução completa

Questão 60

Considere as bases do R 2

γ = - 1,1 , - 1,0

σ = 0,1 , - 1 , - 1

E a transformação linear T : R 2 → R 2 cuja matriz na base γ é:

T γ = 3 - 2 1 - 1

(c) Escreva, se possível, uma forma diagonal de T.

Ver solução completa

Questão 61

Considere as afirmativas:

  1. Se B é invertível, então B T é invertível.
  2. Se A é diagonalizável, então A T é diagonalizável.
  1. (I) é falsa e (II) é verdadeira.
  2. (I) é verdadeira e (II) é verdadeira.
  3. (I) é verdadeira e (II) é falsa.
  4. (I) é falsa e (II) é falsa.

Ver solução completa

Questão 62

A dimensão do núcleo de A - 2 I é 1 e seu polinômio característico é p λ = λ - 2 2 λ + 2 . Assinale a alternativa VERDADEIRA:

a   A dimensão do autoespaço associado ao autovalor 2 é igual a 2

b   A matriz A é diagonalizável.

c det ⁡ A = 0

d   A dimensão do autoespaço associado ao autovalor 2 é igual a 1

Ver solução completa

Questão 63

As matrizes dos enunciados abaixo têm todos os autovalores reais.

  1. Seja A ∈ M 7 × 7 uma matriz não diagonalizável. Suponha que dois dos autovalores de A tenham autoespaços de dimensão 3 e 2 respectivamente. Então A tem exatamente 2 autovalores distintos.
  2. Se A ∈ M 5 × 5 possui exatamente 4 autovalores distintos, então A não é diagonalizável.

a   Ambas são verdadeiras.

b   A afirmação I I é falsa e a I é verdadeira.

c   Ambas são falsas.

d   A afirmação I é falsa e a I I é verdadeira.

Ver solução completa

Questão 64

Seja T a projeção ortogonal do R 3 no plano 2 x + 3 y - z = 0 , seguida da multiplicação por 4 . Assinale a afirmativa VERDADEIRA:

( a ) Os autovalores de T são 4 ,   1 e 0

( b ) Os autovalores de T são 4 ,   - 4 e 0

( c ) Os autovalores de T são 4 ,   0 e 0

( d ) Os autovalores de T são 4 ,   4 e 0

Ver solução completa

Questão 65

A dimensão da imagem de A é 2 e seu polinômio característico é p λ = - λ 2 λ - 1 . Assinale a alternativa VERDADEIRA

( a ) A dimensão do autoespaço associado ao autovalor 1 é igual a 2

( b ) A matriz A é diagonalizável

( c ) det ⁡ A + I = 0

( d ) A dimensão do autoespaço associado ao autovalor zero é igual a 1

Ver solução completa

Questão 66

Seja T : P 2 R → P 2 ( R ) um operador linear tal que:

K e r T - 2 I = 1 + t ,   1 - t 2                 e                 K e r T - I = [ 1 + t + t 2 ]

Em que I :   P 2 R → P 2 ( R ) denota a transformação identidade. Considere a base B = { 1 , t , t 2 } de P 2 ( R ) . Se

T 333 B = a b c d e f g h i

Então a + d será igual a:

  1. 2 - 2 333
  2. 2 334
  3. 1 - 2 333
  4. 1 + 2 334
  5. - 2 333

Ver solução completa

Questão 67

Considere o plano π em R 3 que passa pela origem de equação cartesiana

π : 2 x - y - 2 z = 0

e a transformação linear E : R 3 →   R 3 espelhamento (ou reflexão) em relação ao plano π . Denote por E ε a matriz de E na base canônica.

(d) Seja B uma matriz ortogonalmente diagonalizável. Mostre que B = B T .   Para isso lembre da forma L M N T = N T M T L T .

(e) Considere uma transformação linear M : R 3 → R 3 que tem uma base ortonormal de autovetores e determinante 0. Seja:

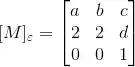
A matriz de M na base canônica. Determine os valores de a,b,c e d.

Ver solução completa

Questão 68

Sejam A =   1 0 0 2 0 0 0 1 0 e A t sua transposta.

Considere   T : R ³ → R ³ a transformação linear cuja matriz, na base canônica R ³ , é a matriz

T = A A t .

e) T é injetora?

f) T é ortogonalmente diagonalizável? Se sua resposta foi afirmativa, diagonalize T ortogonalmente. Se sua resposta foi negativa, justifique.

g) Considere a transformação composta F = T O T . Existe uma base ortonormal de R ³ , feita de autovetores F?

Ver solução completa

Questão 69

15. Considere a base B = 1 ,   77 ,   45 , 0 ,   9 ,   33 , 0 ,   0 ,   877 de R 3 e o operador linear T : R 3 → R 3 tal que:

T B = 3 - 1 1 1 1 1 1 3 1

Assinale a alternativa correta:

(a) T é diagonalizável e os autovalores de T são 2 , 3 + 17 2 e 3 - 17 2 ;

(b) T não é diagonalizável e os autovalores de T são 2 , 17 e -   17 ;

(c) T não é diagonalizável e os autovalores de T são 2 e 1 ;

(d) T é diagonalizável e os autovalores de T são 2 e 5 ;

(e) T é diagonalizável e os autovalores de T são 2 , 17 e -   17 .

Ver solução completa

Questão 70

A matriz 2 × 2 que tem autovetores 3,2 e 5,7 associados, respectivamente, aos autovalores π e 2 é:

a   3 5 2 7 π 0 0 2 3 5 2 7 - 1

b   3 5 2 7 - 1 π 0 0 2 3 5 2 7 - 1

c   3 5 2 7 2 0 0 π 3 5 2 7 - 1

d   3 2 5 7 - 1 π 0 0 2 3 2 5 7

Ver solução completa

Questão 71

Suponha, por simplicidade, que todo brasileiro ou vive no Brasil ou vive na Europa. Todo ano, 30 % dos brasileiros que vivem no Brasil emigram para a Europa, e 20 % dos brasileiros que vivem na Europa imigram de volta para o Brasil. Qual será a percentagem aproximada do conjunto total de brasileiros que, em dez anos, estarão vivendo na Europa?

  1. 60 % .
  2. 45 % .
  3. 51 % .
  4. 75 % .

Ver solução completa

Questão 72

QUESTÃO EXTRA

Seja A uma matriz quadrada, não-nula, e talque A v → . v → = 0 ,   ∀ v → :

  1. A é simétrica
  2. A é invertível
  3. A possui um autovalor positivo
  1. Apenas I é verdadeira
  2. Todas são falsas
  3. Apenas II é falsa
  4. Apenas III é verdadeira
  5. Apenas II é verdadeira
  6. Todas são verdadeiras
  7. Apenas I é falsa

Ver solução completa

Questão 73

Sejam a ,   b ,   c   ∈   R tais que   2   e   4 sejam os autovalores da matriz A

A = a c c b

e seja fixado um sistema de coordenadas   Σ   =   ( O ,   B ) no plano, com   B   uma

base ortonormal. Considere a elipse de equação:

a x 2   +   b y 2   +   2 c x y   =   1

Uma equação reduzida para essa elipse é:

  1. u 2 2 + v 2 4 = 1
  2. 2 u 2 + 2 v 2 = 1
  3. 2 u 2 + v 2 = 1
  4. 4 u 2 + 2 v 2 = 1
  5. u 2 2 + v 2 2 = 1

Ver solução completa

Questão 74

Sejam A , B e C matrizes quadradas tal que C = A B :

  1. Se A e B são diagonalizáveis, então C é diagonalizável.
  2. Se A e B não são diagonalizáveis, então C não é diagonalizável.

( a ) I é verdadeira e I I é falsa

( b ) I é falsa e I I é falsa

( c ) I é falsa e I I é verdadeira

( d ) I é verdadeira e I I é verdadeira

Ver solução completa

Questão 75

Seja T : R 3 → R 3 um operador linear e seja A ∈ M 3 ( R ) a matriz de T em relação à base canônica de R 3 . Se

K e r T = 1 , - 2,0 ,     K e r T - 2 I = 0,0 , 1 ,                   K e r T - 5 I = [ ( 2,1 , 0 ) ]

Em que I denota o operador identidade de R 3 , então a soma de todos os elementos de A é igual a:

Escolha uma opção:

  1. 16
  2. 9
  3. 11
  4. 13
  5. 10

Ver solução completa

Questão 76

Seja P 3 o espaço dos polinômios de grau menor ou igual a 3 . Seja L : P 3 → P 3 a transformação linear dada por L p x = p ' ' x + x p ' x . Examine quais das afirmações abaixo são verdadeiras. (Sugestão: monte a matriz da transformação na base canônica de P 3 .)

  1. L é diagonalizável;
  2. L é invertível.

( a ) I é falsa e I I é verdadeira

( b ) I é verdadeira e I I é falsa

( c ) Ambas são falsas

( d ) Ambas são verdadeiras

Ver solução completa

Questão 77

Qual matriz abaixo é diagonalizável (sobre os reais)?

(a)

(b)

(c)

(d)

Ver solução completa

Questão 78

Seja A uma matriz qualquer.

Assinaline a alternativa FALSA:

a   Se A é inversível então A T é inversível

b   Se A é injetora então A T é injetora

c   Se A é simétrica então A T é simétrica

d   Se A é diagonalizável então A T é diagonalizável

Ver solução completa

Questão 79

Seja A = a 1 0 a a matriz associada a uma transformação linear T. Para quais valores de a T é diagonalizável?

Ver solução completa

Questão 80

Seja T : R 2 → R 2 uma transformação linear tal que

  • T j = 2 ,   3
  • O vetor i é um autovetor de T e
  • O determinante de T é 4 . Determine:

  1. A matriz T ε   de T na base canônica;
  2. Uma forma diagonal D de T .

Ver solução completa

Questão 81

Considere a transformação linear T : R 3 → R 3 cuja matriz na base canônica é:

T ε = 1 1 1 2 2 2 3 3 3

  1. Determine os autovalores de T .
  2. Determine se T é diagonalizável. Em caso afirmativo, determine uma forma diagonal de T . Em caso negativo, explique porque T não é diagonalizável.

Ver solução completa

Questão 82

Sabe-se que A é uma matriz 5 × 5 diagonalizável e que seus autovalores são apenas 2 ,   3 e 4 . A única opção que PODE SER correta é:

  1. dim ⁡ i m a g e m A = 3
  2. dim ⁡ n u c l e o A - 2 I = 3
  3. dim ⁡ i m a g e m A = 4
  4. dim ⁡ n u c l e o A - 2 I = 4

Ver solução completa

Questão 83

Seja A uma matriz não invertível que satisfaz A 1 ,   2 = 2 ,   4 , então:

  1. A é diagonalizável.
  2. A é ortogonal.
  3. A é diagonal.
  4. A é simétrica.

Ver solução completa

Questão 84

Considere as afirmativas:

  1. Se T : R 6 → R 6 possui 6 autovalores distintos então T é diagonalizável.
  2. Se R : R 5 → R 5 é diagonalizável então R possui 5 autovalores distintos.
  1. (I) é falsa e (II) é verdadeira.
  2. (I) é falsa e (II) é falsa.
  3. (I) é verdadeira e (II) é verdadeira.
  4. (I) é verdadeira e (II) é falsa.

Ver solução completa

Questão 85

Considere as seguintes afirmações:

  1. Se n for um inteiro positivo, A ,   B ∈ M n ( R ) forem matrizes diagonalizáveis e os polinômios característicos de A e B forem iguais, então A e B serão semelhantes;
  2. Se n for um inteiro positivo, A , B ∈ M n ( R ) forem matrizes semelhantes e A for simétrica, então B será simétrica
  3. Se V for um espaço vetorial munido de um produto interno e se T : V → V e S : V → V forem operadores lineares simétricos, então o operador T ∘ S + S ∘ T será simétrico.

Assinale a alternativa correta:

  1. Apenas as afirmações ( I ) e ( I I I ) são verdadeiras;
  2. Apenas as afirmações ( I ) e ( I I ) são verdadeiras;
  3. Apenas a afirmação ( I ) é verdadeira;
  4. Todas as afirmações são falsas;
  5. Todas as afirmações são verdadeiras.

Ver solução completa

Questão 86

Considere as seguintes afirmações:

  1. Se n for um inteiro positivo e A , B ∈ M n ( R ) forem matrizes com o mesmo determinante, então A e B serão semelhantes;
  2. Se V for um espaço vetorial tal que dim ⁡ V = 1777 , I :     V → V denotar a transformação identidade e T :     V → V for uma transformação linear tal que 55 e 99 sejam autovalores de T e tal que dim ⁡ K e r ( T - 55 I ) = 1776 , então T será diagonalizável;
  3. A matriz

77 43 0 0 77 43 0 0 77

É diagonalizável.

Assinale a alternativa correta:

  1. Apenas a afirmação ( I I ) é verdadeira;
  2. Todas as afirmações são verdadeiras;
  3. Apenas as afirmações I e ( I I ) são verdadeiras;
  4. Apenas as afirmações I I e ( I I I ) são verdadeiras;
  5. Apenas as afirmações I e ( I I I ) são verdadeiras;

Ver solução completa

Questão 87

(I) A matriz 1 4 - 1 5 0 0 0 0 0 0 0 0     3 0     0 2 cujo polinômio característico é λ - 3 3 ( λ - 2 ) , é diagonalizável.

(II) Se uma matriz 3 × 3 tem polinômio característico ( 3 - λ ) ( 2 - λ ) ( 1 - λ ) , então é diagonalizável.

(a) (I) e (II) são falsas.

(b) (I) e (II) são verdadeiras.

(c) (I) é falsa e (II) é verdadeira.

(d) (I) é verdadeira e (II) é falsa.

Ver solução completa

Questão 88

Considere a matriz

A = 1 2 - 2 0 - 1 1 - 4 0 0

Afirmamos que existem uma matriz invertível P e uma matriz diagonal D tais que

P - 1 A P = D

Qual dos itens abaixo nos dá P e D corretas?

( a ) P = 0 - 3 - 3 1 1 2 1 4 - 4 e D = - 3 0 0 0 3 0 0 0 0

( b ) P = 0 - 3 - 3 1 1 2 1 4 - 4 e D = 0 0 0 0 3 0 0 0 - 3

( c ) P = - 3 0 - 3 1 1 2 4 1 - 4 e D = - 3 0 0 0 3 0 0 0 0

( d ) P = - 3 0 - 3 1 1 2 4 1 - 4 e D = 0 0 0 0 3 0 0 0 - 3

Ver solução completa

Questão 89

Sejam T : R 2 → R 2 e S :   R 2 → R 2 operadores lineares tais que:

1,2 ∈ K e r 1 2 T + S - 2 I                   - 1 , - 3 ∈ K e r 1 2 T + S + I

E S x , y = x + y ,   x + 2 y ,   ∀ ( x , y ) ∈ R 2 , em que I :   R 2 → R 2 denota a transformação identidade. Dados ( x , y ) ∈ R 2 , temos que T ( x , y ) é igual a:

  1. 14 x - 8 y ,   34 x - 18 y ;
  2. 14 x - 20 y ,   10 x - 18 y ;
  3. 7 x - 4 y ,   17 x - 9 y ;
  4. 7 x - 10 y ,   5 x - 9 y ;
  5. 28 x - 16 y ,   20 x - 36 y .

Ver solução completa

Questão 90

Sejam V um espaço vetorial de dimensão finita e T :   V → V um operador linear diagonalizável. Suponha que o polinômio característico de T seja p T t = t 754 e considere as seguintes afirmações:

  1. O operador T é nulo;
  2. dim ⁡ V = 754 ;
  3. Existem infinitas bases B de V tais que a matriz T B seja diagonal.

Assinale a alternativa correta:

  1. Todas as afirmações são verdadeiras;
  2. Apenas as afirmações (II) e (III) são verdadeiras;
  3. Apenas a afirmação (II) é verdadeira;
  4. Apenas as afirmações (I) e (II) são verdadeiras;
  5. Apenas as afirmações (I) e (III) são verdadeiras;

Ver solução completa

Questão 91

A transformação linear T realiza a projeção ortogonal dos vetores de R 3 no plano 2 x - 5 y + 8 z = 0 , seguida da multiplicação por 2 . Então é FALSO afirmar que:

a   O posto de T é igual a 2

b   T não é invertível

( c ) T é diagonalizável

( d ) 1 e 0 são autovalores de T

Ver solução completa

Listas de Exercícios Resolvidos

Lista de Introdução às EDO'sLista de Subespaços VetoriaisLista de ElipsesLista de Parábolas Lista de Ângulos entre RetasLista de Combinação LinearLista de Posições Relativas de RetasLista de Expressão Analítica de uma TLLista de Reflexão OrtogonalLista de Escalonamento

Principais Conceitos de Álgebra Linear e Geometria Analítica

Equação da Esfera