Equação do Plano
Produzido por Aline BuzziTeoria
Fala aí, nós somos o Responde Aí, a maior plataforma de exatas do Brasil, e estamos aqui para salvar o seu semestre.
Hoje iremos te mostrar e ajudar você a entender a equação do plano. Esse é um conteúdo estudado na disciplina álgebra linear e geometria analítica, mas também aparece nos cálculos.
Equação do Plano
A equação do plano nada mais é que a forma matemática de representarmos um plano.
Primeira pergunta: Você sabe o que é um plano?
Talvez você esteja lendo esse conteúdo sentado à mesa e quando você olha para o topo da mesa, o que você vê é um plano.
Basicamente, é uma superfície lisa e com apenas duas dimensões.
A gente pode definir um plano através daquelas definições hiper mega formais que encontramos em livros, mas covenhamos que elas não ajudam muito, não é? kkkkkk
Agora que sabemos o que é um plano, nos deparamos com a segunda pergunta: Como definir um plano?
Para definirmos um plano precisamos conhecer duas coisas:
- um vetor normal ao plano, que denotamos por
, e; - um ponto que pertença a esse plano, que podemos chamar de
.
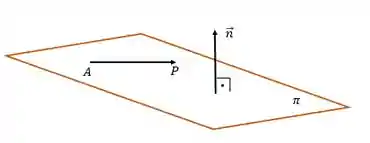
Tendo conhecido essas duas coisinhas nós conseguimos encontrar o que chamamos de equação geral do plano ou equação cartesiana do plano, como mostra o quadro abaixo:

Vamos entender melhor isso com um EXEMPLO: Seja um plano
Bom, para encontrar a equação do plano precisamos achar são os valores das constantes
Como as constantes
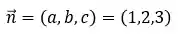
Então, temos que:
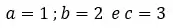
Agora podemos pegar esses valores e substiruir na equação:
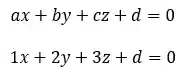
Mas ainda falta a constante
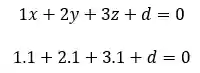
Assim, podemos isolar o
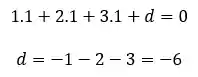
Com isso, a gente encontra a equação geral do plano:
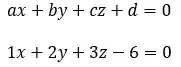
Beleza, tranquilinho, não é?
Mas e se ao invés de termos um ponto e um vetor normal, for conhecido um ponto
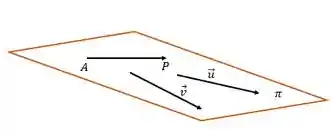
Conseguiremos achar a equação geral com essas informações?

SIM, claro que conseguiremos, mas precisamos usar um método diferente.
Vamos supor que o ponto conhecido é novamente
Passo 1
Definir um vetor
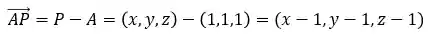
Passo 2
Vamos fazer o produto misto entre os vetores
Montando o produto misto para o nosso exemplinho teremos:

Resolvendo o produto misto e igualando a zero, temos:

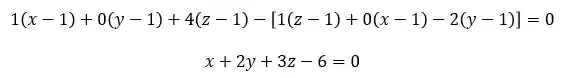
📢ALERTA: Note que para encontrar a equação do plano usando esse segundo método é importante saber fazer o produto misto entre vetores, então caso você ainda não saiba ou não se lembra muito bem é só conferir essa nossa página aqui: Produto Misto
A equação que obtivemos por esse segundo método é exatamente a mesma que obtivemos antes, e isso não é coincidência, porque se estamos falando do mesmo plano, não importa o método que utilizamos para encontrar a equação ela é sempre a mesma, show de bola?
Essa é a equação do plano e temos esses dois modos de obtê-la. Agora que você já sabe esse conteúdo você pode avançar nos seus estudos e visitar essa nossa página aqui que fala da posição entre planos 👉🏽 Posição entre Planos.
Ou você pode fixar ainda mais esse conteúdo assistindo o vídeo que vou deixar aqui feito por nós do Responde Aí. Nesse vídeo você vai aprender esse conteúdo de forma direta, descontraída e clara. 😉
Vídeo
Vídeo
Exercícios Resolvidos
Exercício Resolvido #1
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 144-5.
Dê uma equação vetorial do plano que tem por equações paramétricas
Passo 1
O problema nos dá as 3 equações paramétricas do plano. E, nós queremos descobrir qual é a equação vetorial. Bateu o desespero? Calma, vamos devagar para você entender direitinho!!
![]()
Primeiro, temos que retirar todas as informações possíveis que estão nas equações paramétricas. Então, vamos começar!!
Passo 2
As equações paramétricas tem o seguinte formato:
Sendo que são as coordenadas de um ponto que pertence ao plano e e são as coordenadas dos vetores pertencentes ao plano. Sabendo disso e comparando com a equação paramétrica conseguimos obter esses dados.
Comparando, temos:
Passo 3
Bom, na teoria vimos que a forma genérica da equação vetorial do plano é:
Sabemos que é um ponto genérico , o ponto é um ponto conhecido pertencente ao plano, ou seja, e os vetores e são os vetores paralelos ao plano, e
Agora, é só substituirmos:
Resposta
Exercício Resolvido #2
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 152-4.
Determinar a equação geral do plano que passa pelo ponto e é paralelo aos vetores e .
Passo 1
Esse exercício é para esquentarmos bem nossos motores!!haha
O problema nos dá três informações: o ponto que pertence ao plano, e dois vetores paralelos ao plano e . Pela teoria vimos que quando queremos a equação geral e temos um ponto e dois vetores paralelos ao plano basta fazermos o produto misto entre o vetor formado pelo ponto conhecido e um ponto genérico , e os vetores paralelos e igualar a zero.
Passo 2
Então, vamos montar o produto misto entre . Antes, vamos determinar .
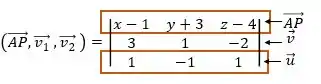
Passo 3
Agora que montamos o produto misto é só resolver:
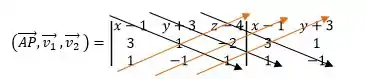
Pronto, chegamos no que queríamos, na equação geral do plano. Podemos também escrever a equação multiplicada por , que ficaria:
As duas estão corretas, o que muda é o sentido do vetor normal, um está apontando para cima e o outro para baixo.
Resposta
Exercício Resolvido #3
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 147-1.
Escrever a equação cartesiana do plano que passa pelo ponto e é paralelo ao plano:
Passo 1
O enunciado nos pede a equação cartesiana do plano , sendo que devemos determinar essa equação sabendo que o plano passa pelo ponto e que o plano é paralelo ao plano . Bem, parece que está faltando informação?! Pode até parecer, mas temos tudo o que precisamos! Vamos descobrir o que falta!!
![]()
Vamos raciocinar o que podemos tirar de informação do plano !! Bem, temos a equação geral do plano e dela podemos tirar o vetor normal ao plano , certo? Pois, sabemos que a equação geral do plano tem a seguinte forma:
Sendo e as coordenadas do vetor normal do plano , . O problema falou que os planos e são paralelos, então isso significa dizer que o vetor normal ao plano também é normal ao plano . Pronto matamos a charada!!!
Passo 2
Agora que sacamos que o vetor normal de é normal também à , então temos tudo o que precisamos para determinar a equação geral do plano . Assim, sabendo:
Substituindo as coordenadas de na equação geral temos:
Passo 3
Só falta descobrirmos o valor de substituindo :
Então, nossa equação é:
Resposta
Exercício Resolvido #4
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 153-5.
Estabelecer a equação geral do plano determinado pelos pontos e .
Passo 1
Esse problema é parecido com o anterior que fizemos, pois o exercício nos pede novamente a equação geral do plano. Porém, o enunciado nos fornece 3 pontos que determinam o plano que queremos. Que estanho!! Como faço isso tendo apenas 3 pontos? Na teoria não lembro de ter visto nada disso!! Realmente, você ainda não viu!! Mas, você vai ver como é possível fazer isso!!

Passo 2
Vamos analisar a figura a seguir
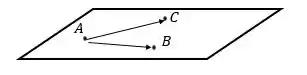
Com os três pontos e pertencentes ao plano conseguimos formar dois vetores que sejam paralelos ao plano, por exemplo, os vetores e . Assim, teríamos dois vetores paralelos ao plano e ainda podemos escolher um dos 3 pontos para achar a equação geral do plano fazendo o produto misto.
Então, vamos primeiro calcular os vetores e .
Passo 3
Agora, já temos dois vetores paralelos ao plano e não são paralelos entre si. Falta escolher um ponto para fazer o produto misto. Porquê eu quero vou escolher o ponto . Então, bora montar o produto misto. Lembrando que o terceiro vetor é formado pelo ponto e o ponto genérico que gera .
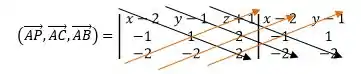
Para tornar os índices os mais reduzidos podemos multiplicar por e obteremos:
Prontinho, chegamos na equação geral. Lembrando que os vetores paralelos poderiam ter sido outros que o resultado daria no mesmo, bem como o ponto escolhido.
Ainda, há uma segunda forma de se resolver esse problema que é ao invés de zerar o produto misto, poderíamos fazer o produto vetorial entre os vetores paralelos ao plano encontrados e assim acharíamos o vetor normal ao plano. Escolheríamos um ponto e substituiríamos direto na equação geral do plano .
Resposta
Exercício Resolvido #5
Prova de Segunda chamada da Unicamp. 1º semestre de 2013. Questão 4.
O ponto tem coordenadas e a reta passa pelo ponto e é paralela ao vetor . Mostrar que não pertence à reta e determinar a equação do plano que contém e .
Passo 1
O enunciado nos fornece várias informações!! Vamos retirar!!
Dados:
Tendo esses dados devemos mostrar que o ponto não pertence à reta e também devemos determinar a equação do plano que contém e .
Passo 2
Vamos começar mostrando se o ponto pertence ou não á reta . Para isso, como vimos no tópico sobre “Estudo da Reta” devemos montar alguma das equações da reta e testar. Como temos o vetor diretor que é o paralelo a reta e um ponto, vou montar as equações simétricas da reta e testar o ponto .
Substituindo os valores de e , temos:
Passo 3
Agora que já temos as equações simétricas da reta basta substituirmos os valores de e verificar a validade das equações:
Portanto, mostramos que não pertence à
Passo 4
Para finalizar, devemos determinar a equação geral do plano que contém a reta e o ponto
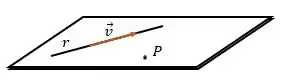
A figura acima mostra o que temos de informações, ou seja, a reta e o ponto que pertence ao plano e sabemos que não pertence à . Mas, vimos que para determinar um plano precisamos do vetor normal e um ponto, ouuu, de dois vetores paralelos ao plano e um ponto. Bem, essa segunda opção me parece a mais viável para o nosso caso!! Um vetor paralelo nós já temos que é o vetor , mas precisamos de mais um!!! Como achar? Se encontrarmos um ponto pertencente à reta e fizermos um vetor com o ponto , teremos:
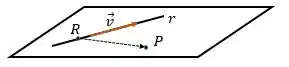
Então, bora achar o ponto pertencente à reta . Para isso vamos usar as equações simétricas que já achamos:
Se chutarmos que , teremos que:
Então, devemos achar e de forma que a proporção seja , assim:
Portanto, temos o ponto .
Passo 5
Agora podemos encontrar o vetor e então teremos as informações necessárias para encontrar a equação geral do plano.
Agora é só montar o produto misto entre o ponto e um ponto genérico e os vetores e .
Montando o produto misto, temos:
Resolvendo,

Vale ressaltar que o ponto da reta escolhido poderia ter sido qualquer outro, que o resultado deve ser o mesmo. Pois, o que importa realmente é que os dois vetores não sejam paralelos entre si e como o ponto não pertence à então não corremos esse risco ;)
Resposta
Exercício Resolvido #6
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 181-18.
Determine a equação geral do plano que contém os pontos e e é perpendicular ao plano
Passo 1
Queremos determinar a equação geral do plano que contém os pontos e e ainda é perpendicular ao plano , ou seja, forma . Nossa de novo determinar a equação geral do plano??

Isso mesmo!! Porém, a cada questão estamos vendo que o enunciado pode nos dar diferentes dados e que mesmo assim conseguimos obter a equação geral ;).
Nessa questão, por exemplo, vamos nos basear pela figura a seguir.
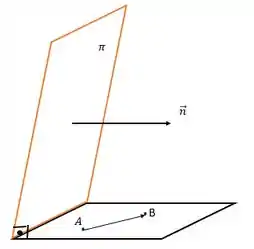
Novamente, para determinar o plano que queremos temos duas opções: ter o vetor normal ao plano e um ponto pertencente a ele OU ter dois vetores paralelos ao plano e um ponto pertencente à ele. Pela figura, podemos ver que vamos ficar com a segunda opção, pois com os pontos e conseguimos formar o vetor que é paralelo ao plano já que eles pertencem ao plano e também podemos notar que o vetor normal do plano é paralelo ao plano que queremos determinar, pois os dois são perpendiculares.
Passo 2
Com tudo o que falamos, acho que deu para sacar que nossos dados serão o vetor , o e um dos pontos ou que poderemos escolher qualquer um deles que o resultado será o mesmo. Vamos determinar então os vetores e :
O vetor tiraremos da equação geral do plano :
Por fim, o ponto que usaremos será o , lembrando que poderia ser o .
Passo 3
Agora, basta montarmos o produto misto entre os vetores e . Sendo um ponto genérico.
Resolvendo:
Prontinho, encontramos a equação geral do plano!!

Resposta
Exercício Resolvido #7
Lista 7. UFF. Exercício 6
Ache o ponto de interseção da reta , que passa pelos pontos e , com o plano que tem como vetor normal e passa pelo ponto .
Passo 1
O problema nos dá os seguintes dados.
Dados: Reta Plano
Com esses dados devemos determinar o ponto de interseção entre a reta e o plano. Ahh??! Como assim? Calma!!! Lembra que lá na teoria falamos que íamos explicar direitinho no exercício?!! Então, a hora chegou!!
![]()
Bom, para começar devemos determinar as equações da reta e do plano. Mas, quais equações? Para ser mais fácil determinar o ponto de interseção, é melhor acharmos a equação geral do plano e as equações reduzidas da reta. Mais para frente ficará mais claro o porquê de escolhermos essas equações.
Passo 2
Vamos começar pelas equações reduzidas da reta. Porquê eu quero que você entenda como montar as equações reduzidas em função de vou achar as equações reduzidas da reta em função de . Como vimos, na teoria as em função de , vamos relembrar como chego nas em função de . Sabemos que as reduzidas provêm das simétricas, então:
Como quero em função de , escreverei:
Isolando e , teremos:
Já sabemos a equação reduzida, basta substituirmos os valores de e . Como nos é dados dois ponto que pertencem à reta e , então um vetor diretor pode ser e o ponto podemos escolher entre ou , vou escolher o ponto . Então teremos o seguintes dados:
Substituindo nas equações reduzidas temos:
Passo 3
Agora, vamos determinar a equação geral do plano. Temos, o vetor normal e o ponto que pertence ao plano. Subsituindo os valores de na equação geral do plano temos:
Para acharmos substituiremos .
Assim,
Passo 4
Já temos todas as equações que precisamos! Podem os montar o seguinte sistema de equações:
Para acharmos o ponto que é o ponto da interseção basta acharmos as coordenadas que satisfazem as 3 equações acima. Entendeu agora porque escolhi as equações reduzidas da reta e a equação geral do plano?
Resolvendo o sistema temos que deve ser . Substituindo na equação teremos:
Multiplicando a equação por e somando com a equação teremos:
Agora, para achar o valor de basta substituirmos na equação :
Assim, nosso ponto de interseção é:
Resposta
Exercício Resolvido #8
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 156-7.
Determinar a equação geral do plano que contém as retas
e
Passo 1
O enunciado nos dá as equações de duas retas e e diz que essas duas retas estão no plano que queremos determinar a equação geral. Ent��o, para achar a equação geral do plano devemos determinar dois vetores paralelos ao plano e um ponto pertencente à ele. Os dois vetores paralelos podemos obter por meio do vetor diretor de cada reta.
Vamos começar descobrindo qual é o vetor diretor de cada reta, beleza?!
Passo 2
A reta está escrita na forma de equações reduzidas em função de . Por meio delas conseguimos determinar o jeito genérico dos pontos pertencentes à reta:
Se encontrarmos 2 pontos da reta , conseguimos formar o vetor diretor da mesma, assim:
Assim, o vetor diretor da reta é:
então .
Passo 3
A reta nos é dada em equações paramétricas pois todas as coordenadas e estão em função de . Podemos identificar o vetor diretor facilmente nesse caso, basta observar os coeficientes de :
Assim, .
Passo 4
Dessa forma, analisando as duas retas temos dois vetores:
Opa!!! Mas, esses dois vetores são paralelos, pois . Nesse caso não poderemos usar os dois para determinar o plano!! Como faremos então?
Bom, temos a seguinte figura que representa a situação que temos:
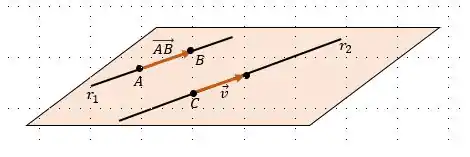
Se e são paralelos, podemos formar um outro vetor que não seja paralelo a eles pegando por exemplo um ponto de e outro de . Por exemplo o vetor !
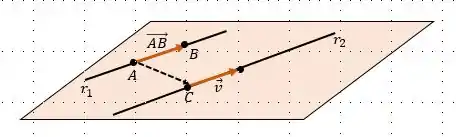
Conseguimos, por meio das suas equações paramétricas, achar um ponto . Com o ponto e , teríamos o vetor:
Assim, escolhendo , entre e já que são proporcionais e o vetor , teremos:
Bom, pelo menos não são proporcionais!!! Ufa!!
Passo 5
Vamos encontrar agora a equação do plano.
Escolhendo como ponto do plano o ponto e os vetores e , agora sim, podemos fazer o produto misto e encontrar a equação geral do plano. Considerando . Teremos .

Pronto!! Chegamos na nossa tão sonhada equação do plano!! hehe

Resposta
Exercício Resolvido #9
Paulo Boulos e Ivan de Camargo e Oliveira, Geometria Analítica: um tratamento vetorial, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 145-5.
Escreva equações paramétricas para os três planos coordenados.
Passo 1
O exercício pede para escrevermos as equações paramétricas dos três planos coordenados. Mas, quais são esses planos ??

Você já os conhece!! Talvez, não esteja lembrando!! Os três planos coordenados, são os planos e , como mostra a figura a seguir:
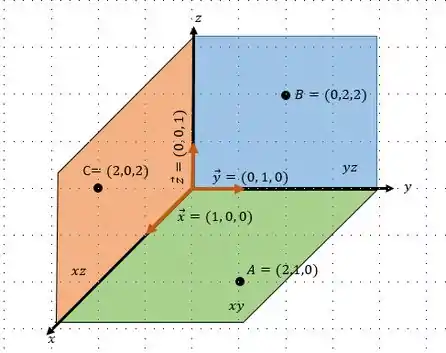
Passo 2
Vamos começar analisando o plano !
Pela figura o plano é o verde. Podemos ver que na figura já desenhamos dois vetores paralelos ao plano que são os vetores e . Poderíamos ter escolhido qualquer outro vetor que pertencesse ao plano. E escolhemos também um ponto qualquer pertencente ao plano que no caso é o ponto . Já temos dois vetores paralelos ao plano e um ponto pertencente ao plano, agora é só colocar os valores nos lugares adequadas da forma paramétrica, que é:
Sabemos, pela teoria que são as coordenadas do ponto pertencente ao plano, no nosso caso é . Já as coordenadas e são as coordenadas dos vetores paralelos ao plano , então podemos dizer que:
Escrevendo na forma paramétrica, temos:
Passo 3
Vamos fazer agora para o plano que está em laranja. O procedimento é o mesmo o que vai mudar é o ponto pertencente ao plano e os vetores paralelos. Os vetores e o ponto são:
Colocando na forma paramétrica teremos:
Passo 4
Para terminar vamos montar as equações paramétricas do plano . Pela figura o ponto escolhido e os vetores são:
Substituindo nas equações paramétricas, temos:
Lembrando, que poderíamos ter escolhido outros pontos e vetores. Os vetores que escolhemos são os mais simples para serem utilizados, já os pontos poderíamos ter escolhidos pontos que estivessem sobre os eixos coordenados, porque assim mais coordenadas seriam ZERO e facilitaria nossas contas!!
Resposta
Equações Paramétricas do Plano :
Equações Paramétricas do Plano :
Equações Paramétricas do Plano
Exercício Resolvido #10
Alfredo Steinbruch e Paulo Winterle, Geometria Analítica, 2ª ed, São Paulo: McGrawHill, 1987. Pp. 185-47.
Determinar as equações paramétricas da reta interseção dos planos:
e
Passo 1
Num dos exercícios anteriores determinamos o ponto de interseção entre uma reta e um plano. Agora, queremos determinar a reta que é formada por meio da intereseção entre os planos e . Esse tipo de exercício tem duas formas básicas de resolução!! Vamos fazer as duas passo a passo para você entender direitinho e ver qual prefere para resolver!!

Passo 2
Vamos começar!!!
Primeira maneira:
Sabemos que a reta interseção ela deve satisfazer as duas equações dos planos, então teremos um sistema de equações:
Com essas duas equações podemos determinar as equações reduzidas da reta interseção. Para isso, vamos escrever as equações em função de . Assim, vamos somar as duas equações, para obter o em função de e depois multiplicar a equação por e somar com a equação para obter em função de Fazendo essas manipulações, teremos:
Com essas equações sabemos que os pontos da reta interseção são:
Tendo o ponto genérico da reta, conseguimos determinar a reta sabendo dois pontos dela. Assim,
Um vetor diretor da reta possível é:
E escolhendo, um dos pontos ou , nos caso escolheremos . Conseguimos escrever as equações paramétricas da reta:
Então as equações paramétricas da reta interseção dos dois planos é:
Passo 3
Segunda maneira:
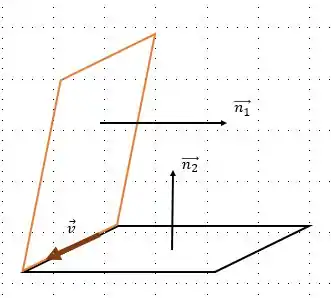
Se nós temos o vetor normal de cada um dos planos, e sabendo que o vetor diretor da reta da interseção é perpendicular entre os dois vetores normais, isso está me lembrando uma coisa!!! Para achar um vetor que seja normal à outros dois fazemos o produto vetorial entre o vetores normais e então encontraremos o vetor . Assim, faremos:
Assim, pelas equações gerais acharemos e :
e
Agora, basta montarmos e resolvermos o produto vetorial: 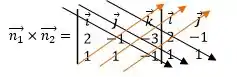
Já sabemos o vetor diretor da reta, agora só falta descobrirmos um ponto pertencente à reta. Para isso vamos usar as duas equações dos planos:
Se a reta deve satisfazer essas duas equações, então se chutarmos pontos que satisfaçam às equações então elas pertencem à reta:
Somando as duas equações, temos:
Para descobrir basta substituirmos em alguma das duas equações, vou escolher a primeira:
Portanto, um ponto que pertence à reta é:
Então, sabendo que o vetor diretor é e o ponto , podemos escrever as equações paramétricas da reta interseção:
Se você notar, o vetor diretor que achamos é o mesmo que encontramos com a primeira forma, porém multiplicado por .