Exercícios de Introdução ao Plano - Lista de Exercícios Resolvida
Questão 3
Ache o ponto de interseção da reta , que passa pelos pontos e , com o plano que tem como vetor normal e passa pelo ponto .
Ver solução completaQuestão 4
Escrever a equação cartesiana do plano que passa pelo ponto e é paralelo ao plano:
Ver solução completaQuestão 5
O ponto tem coordenadas e a reta passa pelo ponto e é paralela ao vetor . Mostrar que não pertence à reta e determinar a equação do plano que contém e .
Ver solução completaQuestão 7
Determinar a equação geral do plano que passa pelo ponto e é paralelo aos vetores e .
Ver solução completaQuestão 10
Determine a equação geral do plano que contém os pontos e e é perpendicular ao plano
Ver solução completaQuestão 11
Um plano em divide o espaço em duas partes, denominadas semiespaços. Considere o plano Qual dos seguintes pontos encontra-se no mesmo semiespaço que o ponto
(a)
(b)
(c)
(d)
Ver solução completaQuestão 12
Considere os pontos e . Determine uma equação para o lugar geométrico dos pontos que são equidistantes de e .
Ver solução completaQuestão 13
Considere as retas em
e .
(a) Encontre a equação cartesiana do plano que contém a reta e o ponto
Ver solução completaQuestão 14
Dados os pontos e e o vetor
a) Escreva equações paramétricas para a reta que contém e é paralela a .
b) Escreva equações paramétricas para o plano que contém a reta e o ponto .
Ver solução completaQuestão 16
Se tal que a interseção dos três planos
é uma reta, então está correto afirmar que:
Questão 17
Na figura são dadas as retas
E o plano . Determine as coordenadas dos pontos , e .
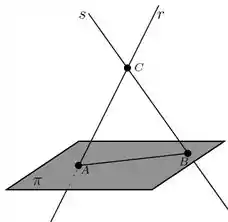
Questão 18
Considere a reta e os planos dados por:
• } ;
• }, onde e são constantes;
• , onde e são constantes;
• , onde e são constantes;
Assuma que e determine os valores das constantes e
Ver solução completaQuestão 19
Considere os pontos
e ,
a reta de equações paramétricas
e o plano suja equação cartesiana é
b) Determine a equação cartesiana do plano que contém a reta e o ponto .
Ver solução completaQuestão 20
Decida quais das afirmações é verdadeira e qual é falsa. Justifique.
- O lugar geométrico dos pontos , tais que , é uma reta.
- Os planos e , são transversais para todo valor de .
- A distância do ponto até a reta de interseção dos planos , e , é menor que 2,5.