Força hidrostática

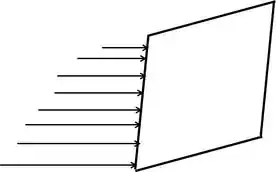
Por isso, podemos escrever em sua forma infinitesimal:

Então, em problemas de pressão hidrostática, eu preciso escrever em função de uma variável que eu consiga integrar. Toda a expressão precisa ficar em função unicamente de uma variável (que será a variável de integração). Todos os outros termos devem ser constantes, que não vão influenciar na variável de integração.

Vamos fazer um exemplo. Esse exemplo é bem completinho e, além do conceito de força hidrostática envolve também o conceito de torque. Vou explicando todos os conceitos durante o exercício, ok? Segura a ansiedade aí! Respira e não pira!

Exemplo: Uma porta com de largura e de altura está localizada em uma parede vertical, plana, de um tanque de água. A porta é articulada ao longo de sua borda superior, que fica abaixo da superfície da água. A pressão atmosférica atua na superfície da porta. Se a pressão na superfície da água for a atmosférica, que força deve ser aplicada na borda inferior da porta a fim de impedi-la de abrir?

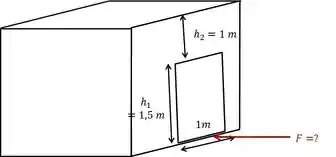
Nesse caso, que quero que a porta fique estática, o que significa que eu quero que o somatório de todas as forças que agem sobre ela seja igual a zero. O primeiro passo a fazer é identificar as forças que agem na porta. As forças que agem sobre a porta são:

• Força F (para segurar)
• Forças de pressão da água e do ar
• Força peso
• Força de resistência da articulação.

Eu quero saber a força mas também não conheço a força da articulação e o peso da porta. Eu preciso de outra equação. Para isso, vou usar outro conceito, que é o de torque. O torque é sempre definido em relação a um ponto em que o objeto irá rodar:

Para que a porta fique estática, a soma dos torques exercidos pelas forças tem que ser igual a zero. Nesses problemas, é sempre importante estabelecer a origem do sistema de coordenadas, lembrando que é você quem escolhe essa origem, o importante é que você seja sempre coerente com ela. Se estabelecermos que o eixo de rotação é localizado no eixo da articulação, que é a borda superior da porta, isso é vantajoso, pois torque é definido como força vezes distância. Nesse caso, a distância da força da articulação em relação ao eixo de rotação é zero, o que significa que o torque será igual a zero.

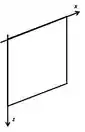
Se no equilíbrio a porta está vertical, isso significa que a força peso não exerce torque.

Portanto, teremos:

Em relação ao ponto de articulação, que escolhemos como sendo coincidente com a borda superior da porta:

Como torque é igual a força vezes distância em relação ao eixo de articulação:

O torque da força de pressão será dado pela força de pressão vezes a distância. Já sabemos que a força de pressão muda em cada ponto da porta, então o conceito é o mesmo de quando escrevemos a força de pressão em sua forma infinitesimal. Poderemos escrever a expressão para o torque da força de pressão também em sua forma infinitesimal:

é a distância da força ao eixo de articulação. Agora temos que estabelecer , isto é, escrevê-la em função de para que possamos integrar

Bom, já sabemos que:

Nesse tipo de problema, temos que avaliar como escrever em função de algo que possamos integrar. Lembre-se que é o elemento infinitesimal de área. Temos que escrever assim porque em cada ponto infinitesimal a força irá mudar!

A porta é um retângulo, certo? Então vamos escrever baseado no sistema de coordenadas que escolhemos anteriormente.

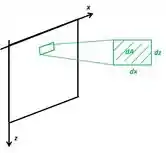
Ok. Então o vai variando. Cada ponto da porta tem uma altura diferente. A largura da porta não importa nesse caso, ela é sempre a mesma independente da altura. Se integrássemos teríamos que integrar de a , que é a largura da porta, e isso daria exatamente . Portanto, podemos esquecer esse .

Ok. Então temos , o que significa que nossa variável de integração é . Portanto, temos que escrever em função da nossa variável de integração. Quem é nesse caso? é sempre a profundidade do ponto em que queremos a força! Lembre-se que a força muda com a profundidade. Nesse caso, ele quer a força que deve ser aplicada na parte inferior da porta. Isso significa que devemos sempre considerar a altura desse ponto .

Colocamos a origem do eixo na parte superior da porta. A profundidade da parte superior da porta em relação à água é fixa e igual a . O que muda é o ponto da porta em que estamos calculando a força em relação à origem do eixo .

Então, concorda que podemos escrever:

Agora já temos a expressão para em função de !! Então podemos voltar para a expressão do torque!

Agora podemos transformar a equação acima em sua forma integrada. Mas, para isso, temos que saber os limites de integração. Como colocamos a origem do eixo na parte superior da porta, esse é o ponto e o ponto final é o ponto inferior da porta, onde estamos querendo calcular a força, que equivale a , pois essa á a altura da porta.

Portanto, temos:

Considerando que a água seja incompressível, isto é que a densidade do fluido não muda com a pressão, então a densidade é constante com a altura e pode sair da integral. corresponde à gravidade e também é constante. Portanto, temos:

Sabemos:

Substituindo os valores, encontramos:

Calma. Eu sei que parece complicado. Mas esse problema é bem completinho, para você entender que esses conceitos de escrever na forma infinitesimal podem ser usados não só para a força em si, mas também podem ser estendidos sempre que uma grandeza varia. O importante é escrever tudo na mesma variável que vai permitir a integração e escolher a origem dos eixos de forma a te facilitar!

Vamos aos exercícios, pois é o treino que leva à perfeição. Não esqueça que ninguém nasce sabendo!