Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Derivadas Direcionais

Ver Todos os Exercícios

Teoria

Opa, bora aprender Derivada Direcional de uma vez por todas!?

O que é uma Derivada Direcional?

Lá atrás, quando a gente aprendeu como o conceito de derivadas a gente viu que uma derivada é uma taxa de variação, isso é… a velocidade na qual uma função varia. Então o que seria uma derivada direcional?

A Derivada direcional pode ser entendida como a velocidade na qual uma função varia numa determinada direção!

Ela tem essa carinha aqui:

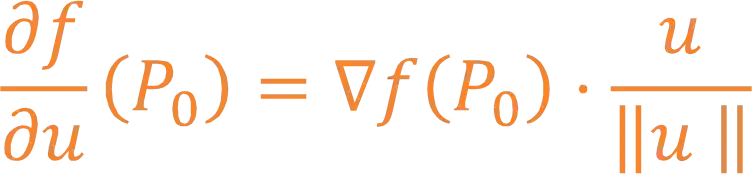
Derivada Direcional.
Derivada Direcional.

Meio assustadora, eu sei! O que temos ai em cima é a derivada de uma função de várias variáveis na direção do vetor u em um ponto e ela vale apenas para funções diferenciáveis!

Te assustei mais ainda?! Foi mal! 🤣 Mas fica tranquilo que a gente vai aprender tudinho sobre derivada direcional…vamos fazer uns exemplos maneiros e tudo vai ficar bem claro! AH, a gente também vai aprender o que fazer quando a gente se deparar com uma função não diferenciável!

Mas antes, existem alguns conhecimentos prévios que você precisa estar crack! Se liga só 👇

⚠️ Derivadas Parciais

⚠️ Vetor Gradiente

Agora sim, vamos ao que interessa!

Como Calcular uma Derivada Direcional

Lá nas derivadas parciais a gente pode calcular a derivada de uma função qualquer em função de e em função de . Mas e se quiséssemos calcular essa derivada em função de e ao mesmo tempo?!

É ai que entra as derivadas direcionais! 🤩

Pra ficar mais claro, vamos olhar de novo a carinha da derivada direcional:

Que se lê: A derivada direcional da função na direção do vetor no ponto é o produto escalar entre o vetor gradiente dessa função em e o vetor unitário da direção do vetor .

Agora vamos pegar uma função e calcular a derivada direcional dela no ponto e na direção do vetor :

Passo 1: Calcular o Vetor Gradiente

Pra a gente achar o vetor gradiente, precisamos derivar nossa função em relação a e a :

Agora com relação a :

Opa, já achamos o gradiente :

Então no ponto temos:

Você também pode acompanhar essa resolução no vídeo abaixo!

Passo 2: Calcular o módulo do vetor

Temos o nosso vetor:

Calculando seu módulo:

Passo 3: Aplicar a fórmula

Substituindo os dados

Calculando:

Então essa é a derivada direcional que queríamos! Viu como é tranquilo?

Maas infelizmente, a vida não é só tranquilidade. Digo isso porque essa fórmula não serve sempre: só podemos usá-la quando a função é diferenciável!

Como Calcular a Derivada Direcional para Funções não Difereciáveis

Nesse caso usamos essa fórmula aqui:

Derivada direcional para funções não diferenciáveis.png
Derivada direcional para funções não diferenciáveis.png

Exemplo: Calcule a derivada direcional para a função

Nesse caso temos:

O módulo de é:

logo:

Calculando, chegamos em:

Prontinho!!

Como Calcular a Derivada Direcional para Funções não Difereciáveis

Exercícios Resolvidos

Exercício Resolvido #1

UFRJ, Cálculo 2, P2 2013.1, questão 1

Encontre a derivada direcional de f x , y , z = x y + y 2 z no ponto P = 7 , - 2,1 na direção do vetor v = 2,2 , 1 .

  1. 2
  2. - 2
  3. 6
  4. - 6
  5. 0
  6. Nenhuma das demais alternativas

Passo 1

Calcular módulo do vetor v :

v = 2 2 + 2 2 + 1 2

⇒ v = 4 + 4 + 1

⇒ v = 9

⇒ v = 3

Passo 2

Calcular vetor gradiente:

f x , y , z = x y + y 2 z

∇ f x , y , z = ∂ f ∂ x , ∂ f ∂ y , ∂ f ∂ z

⇒ ∇ f x , y , z = y ,   x + 2 y z ,   y 2

Passo 3

Calcular vetor gradiente no ponto P :

∇ f x , y , z = y ,   x + 2 y z ,   y 2

∇ f P = ∇ f 7 , - 2,1

⇒ ∇ f P = - 2 ,   7 + 2 - 2 1 ,   - 2 2

⇒ ∇ f P = - 2 ,   7 - 4 ,   4

⇒ ∇ f P = - 2 ,   3 ,   4

Passo 4

Calcular derivada direcional:

∂ f ∂ v P = ∇ f P ⋅ v v  

⇒ ∂ f ∂ v P = - 2,3 , 4 ⋅ 2,2 , 1 3

⇒ ∂ f ∂ v P = 1 3 - 2,3 , 4 ⋅ 2,2 , 1

⇒ ∂ f ∂ v P = 1 3 - 2 2 + 3 2 + 4 1

⇒ ∂ f ∂ v P = 1 3 - 4 + 6 + 4

⇒ ∂ f ∂ v P = 1 3 6

⇒ ∂ f ∂ v P = 2

Alternativa (a).

Resposta

Alternativa (a).

Exercício Resolvido #2

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, exemplo 3.29, p.118

Determine a taxa de variação de f x , y , z = x y z + e 2 x + y no ponto P 0 = - 1,2 , 1 na direção do vetor u = 1,1 , 2 .

Passo 1

Calcular módulo do vetor u :

u = 1 2 + 1 2 + 2 2

⇒ u = 1 + 1 + 2

⇒ u = 4

⇒ u = 2

Passo 2

Calcular vetor gradiente:

f x , y , z = x y z + e 2 x + y

∇ f x , y , z = ∂ f ∂ x , ∂ f ∂ y , ∂ f ∂ z

⇒ ∇ f x , y , z = y z + 2 e 2 x + y ,   x z + e 2 x + y ,   x y

Passo 3

Calcular vetor gradiente no ponto P 0 :

∇ f x , y , z = y z + 2 e 2 x + y ,   x z + e 2 x + y ,   x y

∇ f P 0 = ∇ f - 1,2 , 1

⇒ ∇ f P 0 = 2 1 + 2 e 2 - 1 + 2 ,   - 1 1 + e 2 - 1 + 2 ,   - 1 2

⇒ ∇ f P 0 = 2 + 2 e 0 ,   - 1 + e 0 ,   - 2

⇒ ∇ f P 0 = 4 ,   0 ,   - 2

Passo 4

Calcular derivada direcional:

∂ f ∂ u P 0 = ∇ f P 0 ⋅ u u  

⇒ ∂ f ∂ u P 0 = 4,0 , - 2 ⋅ 1,1 , 2 2

∂ f ∂ u P 0 = 1 2 4,0 , - 2 ⋅ 1,1 , 2

∂ f ∂ u P 0 = 1 2 4 1 + 0 1 + - 2 2

∂ f ∂ u P 0 = 1 2 4 + 0 - 2 2

∂ f ∂ u P 0 = 1 2 4 - 2 2

⇒ ∂ f ∂ u P 0 = 2 - 2

Resposta

∂ f ∂ u P 0 = 2 - 2

Exercício Resolvido #3

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2009, exercício 5 p.120

Sejam

f x , y = x 3 x 2 + y 2 x , y ≠ 0,0 0 x , y = 0,0

E

u = 1,1

  1. Calcule a derivada direcional em u pela definição em 0,0
  2. Calcule a derivada direcional em u pela fórmula do produto escalar em 0,0
  3. Justifique porque os valores encontrados são diferentes.

Passo 1

a)

Vamos começar calculando como ele pede, a derivada direcional pela definição

∂ f ∂ u P 0 = lim t → 0 ⁡ f P 0 + t u - f P 0 t u

Essa conta SEMPRE dá certo, o problema é a fórmula que as vezes não vale!!

Temos

u = 1,1

u = 1 2 + 1 2 = 2

O limite vai ficar

∂ f ∂ u 0,0 = lim t → 0 ⁡ f 0,0 + t 1,1 - f 0,0 t 2 = lim t → 0 ⁡ f t , t - 0 t 2

Lembrando que t → 0 , ou seja ele não é zero, então

f t , t = t 3 t 2 + t 2 = t 3 2 t 2 = t 2

Voltando para o limite

lim t → 0 ⁡ f t , t - 0 t 2 = lim t → 0 ⁡ t 2 t 2 = lim t → 0 ⁡ 1 2 2 = 1 2 2

Passo 2

b)

Vamos agora calcular pela fórmula, primeiro temos que achar o vetor gradiente

∇ f = f x , f y

Como temos uma definição meio estranha da função temos que calcular essa parada pela definição

f x = lim x → 0 ⁡ f x , 0 - f 0,0 x - 0 = lim x → 0 ⁡ x 3 x 2 + 0 2 - 0 x - 0 = lim x → 0 ⁡ x 3 x 2 x = lim x → 0 ⁡ 1 = 1

f y = lim y → 0 ⁡ f 0 , y - f 0,0 y - 0 = lim y → 0 ⁡ 0 3 0 2 + y 2 - 0 y - 0 = lim y → 0 ⁡ 0 y = lim y → 0 ⁡ 0 = 0

Passo 3

A derivada direcional vai ser

∂ f ∂ u 0,0 = ∇ f 0,0 ∙ u u

∂ f ∂ u 0,0 = 1,0 ∙ 1,1 2 = 1 2

Passo 4

c)

Repara que as paradas deram diferentes, porque isso aconteceu? Simples, essa função não é diferenciável.

A resposta que vale é a da definição.

Não precisa rodar muito sobre isso porque não é o propósito da questão, mas até daria pra provar que aquele erro muito gigante que calculamos não é 0 .

Resposta

  1. 1 / 2 2
  2. 1 / 2
  3. É diferente porque a função não é diferenciável

Exercício Resolvido #4

Elaboração Própria

Seja uma função f x , y , z diferenciável no ponto x 0 , y 0 , z 0 . Ele possui a seguinte derivada parcial em relação a x

∂ f ∂ x x 0 , y 0 , z 0 = 1

Sabendo que a derivada direcional dessa função na direção u = 1,2 , 3 é

D u = 5

E além disso a derivada direcional desta mesma função na direção v = 3 , - 2,1 é

D v = 4

Determine o valor do vetor gradiente da função f x , y , z no ponto x 0 , y 0 , z 0 .

Passo 1

Ele quer o vetor gradiente dessa função. Mas como vamos acha-lo? Relaxa, vamos começar usando o que ele deu no enunciado, que são as derivadas direcionais na direção do vetor u e na direção do vetor v . Lembra que a derivada direcional leva em conta o vetor gradiente? O caminho é por ai. Primeiro vamos achar o vetor gradiente, já que vamos usar esse rapaz na fórmula da derivada direcional.

∇ f P 0 = f x x 0 , y 0 , z 0 , f y x 0 , y 0 , z 0 , f z x 0 , y 0 , z 0

Já temos uma dessas derivadas, e além disso para facilitar as contas vamos escrever o vetor gradiente assim

∇ f P 0 = 1 , f y , f z

Só para deixar mais bonitinho rs.

Passo 2

Começando pelo vetor u , devemos fazer a fórmula

D u = ∇ f P 0   . u u

Primeiro vamos achar u

u 2 = 1 2 + 2 2 + 3 2

u = 1 + 4 + 9 = 14

Passo 3

A derivada direcional vai ser

D u = 1 , f y , f z   . 1,2 , 3 14

D u = 1 + 2 f y + 3 f z 14

Esse valor já temos

1 + 2 f y + 3 f z 14 = 5

1 + 2 f y + 3 f z = 5 14

Passo 4

Vamos agora para o vetor v

D v = ∇ f P 0   . v v

Primeiro vamos achar v

v 2 = 3 2 + - 2 2 + 1 2

u = 9 + 4 + 1 = 14

Passo 5

A derivada direcional vai ser

D v = 1 , f y , f z   . 3 , - 2,1 14

D v = 3 - 2 f y + f z 14

Esse valor já temos

3 - 2 f y + f z 14 = 4

3 - 2 f y + f z = 4 14

Passo 6

Vamos encontrar o sistema

1 + 2 f y + 3 f z = 5 14 3 - 2 f y + f z = 4 14

Somando as duas equações vamos encontrar

4 + 4 f z = 9 14

f z = 9 4 14 - 1

Passo 7

Vamos substituir esse valor na segunda equação para acharmos f y

3 - 2 f y + 9 4 14 - 1 = 4 14

2 - 2 f y = 4 14 - 9 4 14

2 f y = 2 - 7 4 14

f y = 1 - 7 8 14

Passo 8

Lembra de como é o vetor gradiente?

∇ f P 0 = 1 , f y , f z

Que vai ficar

∇ f P 0 = 1,1 - 7 8 14 , 9 4 14 - 1

Resposta

∇ f P 0 = 1,1 - 7 8 14 , 9 4 14 - 1

Exercício Resolvido #5

UFF, Cálculo IIB, GMA, 2008.2, Lista 8, exercício 9

A temperatura de uma chapa plana é dada por T x , y = x 2 + y 2 , com x e y em c m e T em ℃ . Calcule de quanto ela varia aproximadamente, se caminharmos 1 c m a partir do ponto 3,4 na direção do vetor que faz um ângulo θ   com o semi-eixo x positivo, se:

  1. θ = 30 °
  2. θ = 210 °

Passo 1

A taxa de variação de uma função na direção de um vetor é a sua derivada direcional na direção desse vetor!

Então, a questão se resume a calcular a derivada direcional da função T no ponto 3,4 , na direção do vetor de norma 1 c m que faz ângulos 30 ° e 210 ° com o eixo x .

Para isso, só usar a fórmula da derivada direcional:

D u → T 3,4 = ∇ T x , y . u → u →

Em que u → é o tal vetor de norma 1 c m (por que o enunciado diz que andamos 1 c m em cada direção).

Passo 2

a)

Para o vetor que faz angulo 30 ° , teremos:

u → = 1 c m . cos ⁡ 30 , 1 c m . sin ⁡ 30

Ou seja, apenas decompomos seu módulo nas coordenadas x em y (tipo em coordenadas polares, saca?).

Como seu módulo já é 1 c m , então nem precisamos colocar mais esse u → na equação.

Passo 3

Ok, agora só falta encontrar o vetor gradiente. Para isso, pegamos a função e montamos um vetor com suas derivadas parciais:

T x , y = x 2 + y 2

T x x , y = 2 x

T y x , y = 2 y

∇ T x , y = 2 x , 2 y

Show! Agora só tacar tudo na equação da derivada parcial ;)

Passo 4

D u → T 3,4 = 2 x , 2 y . cos ⁡ 30 , sin ⁡ 30

Ajustando no lado direito o ponto, colocando x = 3 e y = 4 ,

D u → T 3,4 = 2.3,2.4 . cos ⁡ 30 , sin ⁡ 30

Fazendo o produto escalar:

D u → T 3,4 = 6   . 3 2 + 8   . 1 2 = 4 + 3 3

E aí está! Resposta encontrada, taxa de variação de 4 + 3 3 ℃

Passo 5

b)

Vamos repetir a mesma, mesmíssima coisa para a letra b . Recomendo clicar em “esconde aí” e tentar fazer essa sozinho ;) Pode ser trivial, mas faz pra ver se pegou a ideia. Vou até começar a resolução no próximo passo pra você ficar menos tentado(a) :D

Passo 6

Vamos matar logo isso. Pega a equação da derivada:

D u → T 3,4 = ∇ T x , y . u → u →

Como a função é a mesma, esse vetor gradiente não muda! Continua 2 x , 2 y ... Agora temos outro vetor u → , de mesma norma, 1 c m , mas com θ = 210 ° . Então, só colocar esse novo ângulo na equação também. Assim como na letra a , nao precisamos dividir pela norma, por que ela já é 1 !

D u → T 3,4 = 2 x , 2 y . cos ⁡ 210 , sin ⁡ 210

Como o ponto continua sendo 3,4 ,

D u → T 3,4 = 6,8 . cos ⁡ 210 , sin ⁡ 210

Passo 7

Fazendo o produto escalar, já colocando os valores dos cosseno e seno, lembrando que 210 ° tem simetria com 30 ° ,

D u → T 3,4 = - 6 . 3 2 - 4

E pronto, o outro valor da derivada direcional está aí :)

Resposta

  1. 4 + 3 3 ℃
  2. - 4 - 6 . 3 2 ℃

Exercícios de Livros Relacionados

Determine a derivada direcional da função no ponto dado na direção do vetor v. f x , y , z = x y z 3,2 , 6 v = - 1 ,- 2 ,2
Determine a derivada direcional da função no ponto dado na direção do vetor v → . f x , y = 1 + 2 x y , 3 ,4 ,v → = ( 4 ,- 3 )
14.1. É dado o mapa de contornos mostrando a pressão barométrica (em milímetros) às 7:00 horas da manhã do dia 12 de setembro de 1960, quando o Furacão Donna estava ativo. Estime o valor da função pre
Determine a derivada direcional da função no ponto dado na direção do vetor v → . f x , y = ln ⁡ ( x 2 + y ² ) , 2 ,1 ,v → = ( - 1 ,2 ) ²
Determine a derivada direcional de f x , y , z = x y + y z + z x em P 1 , - 1,3 na direção de Q 2,4 , 5 .