Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Vetor Gradiente

Produzido por Matheus dos Santos Soares
Ver Todos os Exercícios

Teoria

Fala aí! Vamos aprender vetor gradiente com o RespondeAí?

Então vamo que vamo!

Para uma dada função, seja de uma, duas, três ou variáveis independentes, podemos calcular para um dado ponto o que chamamos de vetor gradiente.

Tá, mas afinal o que é um vetor gradiente?!

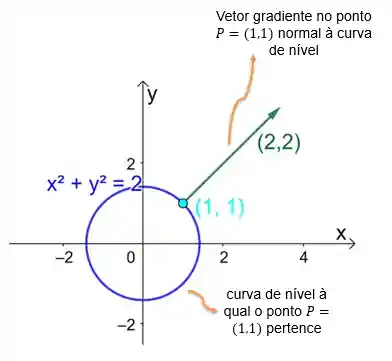
O vetor gradiente é um vetor normal à curva de nível no ponto e indica a direção e sentido que deverá ser deslocada, a partir do ponto especificado, para que haja o maior incremento na grandeza medida.

Parece meio confuso, não é mesmo? Mas fica tranquilo, o que você precisa saber mesmo é como obter esse vetor.

Saber isso vai ser muito importante quando a gente for aprender sobre derivada direcional! Mas um problema de cada vez, agora a gente quer aprender sobre vetor gradiente! 🤣 Então se liga nesse vídeo super completo 👇

Ou vem comigo no textinho, pra descobrir como calcular o vetor gradiente!

Como Calcular o Vetor Gradiente?

Digamos que temos uma função de duas variáveis: . O vetor gradiente de é dado por :

Vamos pegar um exemplo:

Para encontrarmos o vetor gradiente precisamos achar as derivadas parciais em relação a e a .

Então, o vetor gradiente será:

E se a questão pede o vetor gradiente em um ponto específico, como ? Basta substituir o ponto que foi dado:

Graficamente, nós temos o seguinte:

Curva de nível e vetor gradiente no ponto P exemplificado
Curva de nível e vetor gradiente no ponto P exemplificado

Como Calcular um Vetor gradiente em Funções de Várias Variáveis?

Usando a mesma lógica, nós conseguimos calcular o vetor gradiente de funções de várias variáveis, a única coisa que muda é que o vetor terá mais componentes.

Por exemplo, para uma função de três variáveis, , o vetor gradiente será dado por:

E assim por diante...

Propriedades do Vetor Gradiente

Agora, é importante eu apresentar para você algumas propriedades do vetor gradiente que facilitam bastante a vida.

Sejam e funções cujo gradientes são, respectivamente:

E uma constante qualquer, podemos definir as seguintes propriedades:

A parada é que essas propriedades nos ajudam a calcular gradientes de funções que a gente nem conhece a expressão, a partir de gradientes que a gente conhece!

Ou seja, a gente não precisa saber as expressões da , nem da . A gente só precisa saber quem são seus gradientes. Show de bola, né?

Agora você já está fera! Só precisamos praticar com exercícios!😆 💪🏾

Como Calcular o Vetor Gradiente?

Propriedades do Vetor Gradiente

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Determine o vetor gradiente das seguintes funções

  1. f x , y =   x 2 + 3 x y
  2. f x , y , z = 2 x + 4 x y + x z

Passo 1

a )

∇ f x , y =   ∂ f ∂ x ,   ∂ f ∂ y

∇ f x , y = 2 x + 3 y , 3 x

Passo 2

b )

∇ f x , y , z =   ∂ f ∂ x ,   ∂ f ∂ y , ∂ f ∂ z

∇ f x , y , z = 2 + 4 y + z , 4 x , x

Resposta

  1. ∇ f x , y = 2 x + 3 y , 3 x
  2. ∇ f x , y , z = 2 + 4 y + z , 4 x , x

Exercício Resolvido #2

Elaboração Própria

Determine o vetor gradiente das superfícies abaixo

  1. S 1 = x , y , z ∈ R 3 x y z + x 3 + y 3 + z 3 = 3 z
  2. S 2 = x , y , z ∈ R 3 x 2 4 + y 2 9 - z 2 = x

Passo 1

a )

A superfície S 1 é o gráfico da função

f x , y , z = x y z + x 3 + y 3 + z 3 - 3 z

∇ f x , y , z =   ∂ f ∂ x ,   ∂ f ∂ y , ∂ f ∂ z

∇ f x , y , z = y z + 3 x 2 , x z + 3 y 2 , x y + 3 z 2 - 3

Passo 2

b )

A superfície S 2 é o gráfico da função

f x , y , z = x 2 4 + y 2 9 - z 2 - x

∇ f x , y , z =   ∂ f ∂ x ,   ∂ f ∂ y , ∂ f ∂ z

∇ f x , y , z =   x 2 - 1 , 2 y 9 , - 2 z

Resposta

  1. ∇ f x , y , z = y z + 3 x 2 , x z + 3 y 2 , x y + 3 z 2 - 3
  2. ∇ f x , y , z =   x 2 - 1 , 2 y 9 , - 2 z

Exercício Resolvido #3

PUC-RJ, Cálculo 2, P2 2013.2, questão 2, item a

Considere as superfícies

S 1 = x , y , z ∈ R 3 4 y - 2 2 + 3 z - 1 2 = 4

S 2 = x , y , z ∈ R 3 x 3 y 2 + x 3 - 3 y z - z 4 = 3

Explicite as coordenadas de vetores normais não-nulos N 1 x , y , z e N 2 x , y , z às superfícies S 1 e S 2 , respectivamente.

Passo 1

Vamos começar pela superfície S 1 .

Para acharmos um vetor normal temos que, primeiro, achar a função F 1 x , y , z , que é a função da superfície S 1 jogando todas as variáveis para esquerda.

F 1 x , y , z = 4 y - 2 2 + 3 z - 1 2 - 4

O vetor normal vai ser o gradiente dessa nova função F 1 x , y , z

Passo 2

O gradiente vai ser

∇ F 1 = F 1 x , F 1 y , F 1 z

F 1 x = 0

F 1 y = 4.2 y - 2 = 8 y - 16

F 1 z = 3.2 z - 1 = 6 z - 6

O vetor normal vai ser

N 1 = 0   ,   8 y - 16   ,   6 z - 6

Passo 3

Vamos para a superfície S 2 .

Para acharmos um vetor normal temos que, primeiro, que achar a função F 2 x , y , z , que é a função da superfície S 2 jogando todas as variáveis para esquerda.

F 2 x , y , z = x 3 y 2 + x 3 - 3 y z - z 4 - 3

O vetor normal vai ser o gradiente dessa nova função F 2 x , y , z

Passo 4

O gradiente vai ser

∇ F 2 = F 2 x , F 2 y , F 2 z

F 2 x = 3 x 2 y 2 + 3 x 2

F 2 y = 2 x 3 y - 3 z

F 2 z = - 3 y - 4 z 3

O vetor normal vai ser

N 2 = 3 x 2 y 2 + 3 x 2 , 2 x 3 y - 3 z , - 3 y - 4 z 3

Resposta

N 1 = 0   ,   8 y - 16     ,   6 z - 6

N 2 = 3 x 2 y 2 + 3 x 2   ,   2 x 3 y - 3 z   ,   - 3 y - 4 z 3

Exercício Resolvido #4

Elaboração Própria

Sejam

f x , y , z = x 2 2 + x - 3 y z + 4 z

∇ f = x + 1 , - 3 z , 4 - 3 y

g x , y , z = 2 x + 4 x y + 3 y + z

∇ g = ( 2 + 4 y , 4 x + 3,1 )

k = 2

Calcule:

  1. ∇ k f
  2. ∇ f + g
  3. ∇ f - g
  4. ∇ f g

Passo 1

a )

Pela propriedade do vetor gradiente temos

∇ k f = k ∇ f

Então,

∇ k f = 2 . x + 1 , - 3 z , 4 - 3 y = ( 2 x + 2 , - 6 z , 8 - 6 y )

Passo 2

b )

Pela propriedade do vetor gradiente temos

∇ f + g = ∇ f + ∇ g

Então,

∇ f + g = x + 1 , - 3 z , 4 - 3 y + ( 2 + 4 y , 4 x + 3,1 ) = x + 4 y + 3 , - 3 z + 4 x + 3,5 - 3 y

Passo 3

c )

Pela propriedade do vetor gradiente temos

∇ f - g = ∇ f - ∇ g

Então,

∇ f - g = x + 1 , - 3 z , 4 - 3 y - ( 2 + 4 y , 4 x + 3,1 ) = x - 4 y - 1 , - 3 z - 4 x - 3,3 - 3 y

Passo 4

d )

Pela propriedade do vetor gradiente temos

∇ f g = g ∇ f + f ∇ g

Então,

∇ f g = ( 2 x + 4 x y + 3 y + z ) x + 1 , - 3 z , 4 - 3 y + x 2 2 + x - 3 y z + 4 z 2 + 4 y , 4 x + 3,1

∇ f g = 2 x 2 + 2 x + 4 x 2 y + 7 x y + 3 y + x z + z , - 6 x z - 12 x y z - 9 y z - 3 z 2 , 8 x + 10 x y - 12 x y 2 + 12 y - 9 y 2 + 4 z - 3 y z + x 2 + 4 x 2 y 2 + 2 x + 4 x y + 10 y z - 12 y 2 z + 8 z , 2 x 3 + 11 x 2 2 + 3 x - 12 x y z - 9 y z + 16 x z + 12 z , x 2 2 + x - 3 y z + 4 z

∇ f g = 3 x 2 + 4 x + 6 x 2 y + 11 x y + 3 y + 9 z + x z + 10 y z - 12 y 2 z , 2 x 3 + 11 x 2 2 + 3 x + 10 x z - 24 x y z - 18 y z - 3 z 2 + 12 z , x 2 2 + 9 x + 10 x y - 12 x y ² + 12 y - 9 y 2 + 8 z - 6 y z

Resposta

  1. ∇ k f = ( 2 x + 2 , - 6 z , 8 - 6 y )
  2. ∇ f + g = x + 4 y + 3 , - 3 z + 4 x + 3,5 - 3 y
  3. ∇ f - g = x - 4 y - 1 , - 3 z - 4 x - 3,3 - 3 y
  4. ∇ f g = 3 x 2 + 4 x + 6 x 2 y + 11 x y + 3 y + 9 z + x z + 10 y z - 12 y 2 z , 2 x 3 + 11 x 2 2 + 3 x + 10 x z - 24 x y z - 18 y z - 3 z 2 + 12 z , x 2 2 + 9 x + 10 x y - 12 x y ² + 12 y - 9 y 2 + 8 z - 6 y z

Exercícios de Livros Relacionados

a ) Determine o gradiente de f b ) Calcule o gradiente no ponto P c ) Determine a taxa de variação de f em P na direção do vetor u . f x , y , z = x + y z P 1,3 , 1 u = 2 7 , 3 7, 6 7
Determinar o vetor gradiente das funções dadas nos pontos indicados:c) z = s e n( 3 x + y ) ; P 0 , π 2
Determinar o vetor gradiente das funções dadas nos pontos indicados:g) f u ,v ,w = u 2 + v 2 - w 2 + u v w ; P 0,1 ,0
Determine a equação da reta tangente à curva de nível dada, no ponto dado. x 2 + x y + y 2 - 3 y = 1 ,e m 1,2
Determine a função f : R 2 → R cujo gráfico passa pelo ponto ( 1,2 , 1 ) e tal que ∇ f x , y = ( 2 x y 3 - 2 x , 3 x 2 y 2 + 2 y - 1 )