Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Derivadas Parciais

Ver Todos os Exercícios

Teoria

Fala aí! Bora aprender derivadas parciais de uma vez por todas?!

O que é uma Derivada Parcial?

As derivadas parciais aparecem quando começamos a lidar com funções que tem pelo menos duas variáveis!

Como por exemplo:

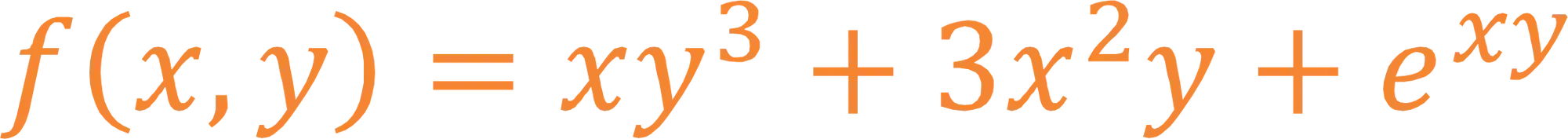
Função de várias variáveis
Função de várias variáveis

Mas e se eu te pedisse para calcular a derivada dessa equação? Hm, você teria que se perguntar, em relação a qual variável eu quero calcular a derivada e é ai que surgem as derivadas parciais.

📢 Clique para ver mais:

Como Resolver uma Derivada Parcial

Quando calculamos a derivada de uma função que possui mais de uma variável, precisamos escolher em relação a qual variável desejamos calcular a derivada. Por exemplo, a função a cima, que possui duas variáveis, possui duas derivadas parciais diferente:

A derivada em relação a :

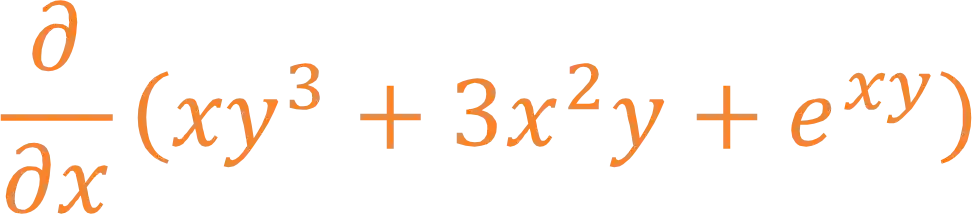
Derivada parcial em relação a x
Derivada parcial em relação a x

E a derivada em relação a :

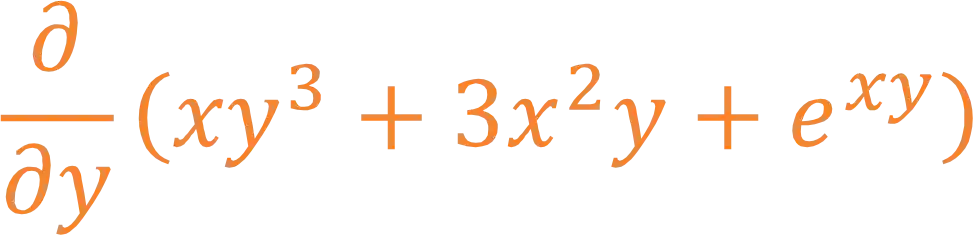
Derivada parcial em relação a y
Derivada parcial em relação a y

-Mas como calculamos cada uma delas? 😖

Pra saber isso e muito mais, se liga nesse videozinho supercompleto sobre Derivadas Parciais que o Responde Aí preparou pra você! 👇 🧡

Passo 1: Identificar as Derivadas Parciais

Esse passo a gente fez ali em cima! Temos a derivada com relação a :

E a derivada com relação a :

Passo 2: Derivar a Função com Relação a

Vamos começar calculando , ou seja, a derivada parcial da função em relação a :

Como é a variável em relação a quem estamos derivando, podemos considerar todas as outras variáveis da função como constantes. Então para a primeira parcela da função eu teria:

Ou seja, considerei como como uma constante, e por isso ela se manteve igual após a derivada.

Para a segunda parcela, novamente derivando em relação a :

Agora para a última parcela, novamente derivando em relação a :

Aqui, não podemos esquecer da regra do peteleco e de pensar o como uma constante, por isso que ele aparece multiplicando quando derivamos em relação a .Então, temos que:

Passo 2: Derivar a Função com Relação a

Para derivar a função em relação a , usamos o mesmo raciocínio da derivação com relação a . Agora tratamos o como constante e derivamos o . Chegamos então em:

Prontinho! Sem mistério!

Derivadas Parciais: Função de Três variáveis

E se ao invés de termos uma função com duas variáveis, tivermos uma função com TRÊS variáveis? Bora resolver um exemplo!

Calcule as derivadas parciais de primeira ordem da função:

Passo 1: Identificar as Três Derivadas Parciais


Para o nosso exercício, temos que identificar as 3 derivadas parciais de primeira ordem que termos que calcular:

Passo 2: Calcular a derivada em relação a

Agora vamos começar calculando nossa derivada parcial em relação a :

Lembrando que tudo que não diz respeito a eu posso considerar um constante, por isso que o último termo some, porque derivada de constante vale zero.

Passo 3: Calcular a derivada em relação a

Calculando a derivada parcial em relação a :

Passo 4: Calcular a Derivada em relação a

Calculando em relação a :

A derivada em relação a é a mais bobinha, mas é a que a galera mais costuma errar, reparem que os dois primeiros termos da função não tem a variável então quando estamos derivando em relação a podemos considerá-los constantes.

Resposta:

Derivadas Parciais: Exercício Resolvido

Agora, bora praticar com mais exercícios?!

Derivadas Parciais: Função de Três variáveis

Derivadas Parciais: Exercício Resolvido

Exercícios Resolvidos

Exercício Resolvido #1

Diomara Pinto e Maria Cândida Ferreira Morgado, Cálculo Diferencial e Integral de Funções de Várias Variáveis, 3ª ed. Rio de Janeiro: UFRJ, 2004, p.102. questão 5, MODIFICADA.

Determine as derivadas parciais de primeira ordem da função:

f x , y , z = x 2 y - 3 x y 2 + 2 y z

Passo 1

Para calcular ∂ f ∂ x consideramos y e z constantes:

∂ f ∂ x = 2 x y - 3 1 y 2 + 0

⇒ ∂ f ∂ x = 2 x y - 3 y 2

Passo 2

Para calcular ∂ f ∂ y consideramos x e z constantes:

∂ f ∂ y = x 2 1 - 3 x 2 y + 2 1 z

⇒ ∂ f ∂ y = x 2 - 6 x y + 2 z

Passo 3

Para calcular ∂ f ∂ z consideramos x e y constantes:

∂ f ∂ z = 0 - 0 + 2 y ( 1 )

⇒ ∂ f ∂ z = 2 y

Resposta

∂ f ∂ x = 2 x y - 3 y 2

∂ f ∂ y = x 2 - 6 x y + 2 z

∂ f ∂ z = 2 y

Exercício Resolvido #2

Lista de Exercício de Cálculo II, seção 3.2, Exercício 98, Letra c

Determine as derivadas parciais de primeira ordem da função:

f x , y = x 3 + y 2 x 2 + y 2

Passo 1

Calculando ∂ f ∂ x :

Regra do quociente:

a b ' = a ' b - a b ' b 2

∂ f ∂ x = x 3 + y 2 ' ⋅ x 2 + y 2 - x 3 + y 2 ⋅ x 2 + y 2 ' x 2 + y 2 2

⇒ ∂ f ∂ x = 3 x 2 + 0 ⋅ x 2 + y 2 - x 3 + y 2 ⋅ ( 2 x + 0 ) x 2 + y 2 2

∂ f ∂ x = 3 x 2 x 2 + y 2 - 2 x x 3 + y 2 x 2 + y 2 2

∂ f ∂ x = 3 x 4 + 3 x 2 y 2 - 2 x 4 - 2 x y 2 x 2 + y 2 2

⇒ ∂ f ∂ x = x 4 + 3 x 2 y 2 - 2 x y 2 x 2 + y 2 2

Passo 2

Calculando ∂ f ∂ y :

Regra do quociente:

a b ' = a ' b - a b ' b 2

∂ f ∂ y = x 3 + y 2 ' ⋅ x 2 + y 2 - x 3 + y 2 ⋅ x 2 + y 2 ' x 2 + y 2 2

⇒ ∂ f ∂ y = 0 + 2 y ⋅ x 2 + y 2 - x 3 + y 2 ⋅ ( 0 + 2 y ) x 2 + y 2 2

∂ f ∂ y = 2 y x 2 + y 2 - 2 y x 3 + y 2 x 2 + y 2 2

∂ f ∂ y = 2 y x 2 + y 2 - x 3 + y 2 x 2 + y 2 2

∂ f ∂ y = 2 y ( x 2 - x 3 ) x 2 + y 2 2

⇒ ∂ f ∂ y = 2 x 2 y ( 1 - x ) x 2 + y 2 2

Resposta

∂ f ∂ x = x 4 + 3 x 2 y 2 - 2 x y 2 x 2 + y 2 2

∂ f ∂ y = 2 x 2 y ( 1 - x ) x 2 + y 2 2

Exercício Resolvido #3

UERJ, Cálculo II, Lista 2, Professora Renata, questão 1, item b.

Determine as derivadas parciais em relação a x e a y , para a seguinte função:

f x , y = e x y   l n x 2 y

Passo 1

Calculando ∂ f ∂ x :

Regra do produto:

a . b ' = a ' . b + b ' . a

∂ f ∂ x = e x y . 1 y ln ⁡ x 2 y + 1 x 2 y . 2 x y . e x y

∂ f ∂ x = e x y 1 y ln ⁡ x 2 y + 2 x

Passo 2

Calculando ∂ f ∂ y :

Regra do produto:

a . b ' = a ' . b + b ' . a

∂ f ∂ y = e x y . - x y 2 ln ⁡ x 2 y + 1 x 2 y . - x 2 y 2 . e x y

∂ f ∂ y = - e x y x y 2 ln ⁡ x 2 y + 1 y

Resposta

∂ f ∂ x = e x y 1 y ln ⁡ x 2 y + 2 x

∂ f ∂ y = - e x y x y 2 ln ⁡ x 2 y + 1 y

Exercício Resolvido #4

UNICAMP, Cálculo II, Exame 2014 Noite, questão 1, item a.

Seja u = x 2 + y 2 ϕ ( x / y ) , em que ϕ   : R → R é uma função diferenciável de uma variável real. Verifique que

x ∂ u ∂ x + y ∂ u ∂ y = 2 u .

Passo 1

Queremos verificar essa relação, que envolve as derivadas parciais de u , então vamos calculá-las! Vamos ter que usar a regra da cadeia e a regra do produto:

∂ u ∂ x = 2 x . ϕ x y + x 2 + y 2 ϕ ' x y 1 y

Repare que x y = x y - 1 então, pra outra derivada parcial vamos ter:

∂ u ∂ y = 2 y . ϕ x y + x 2 + y 2 ϕ ' x y x . - 1 y - 2

O que dá:

∂ u ∂ y = 2 y . ϕ x y + x 2 + y 2 ϕ ' x y - x y 2

Passo 2

-

Show de bola, agora vamos verificar a equação!

x ∂ u ∂ x + y ∂ u ∂ y = x 2 x . ϕ x y + x 2 + y 2 ϕ ' x y 1 y + y 2 y . ϕ x y + x 2 + y 2 ϕ ' x y - x y 2

Poxa, ficou tão grande :( Mas não adianta chorar, agora é arregaçar as mangas e partir pras contas! Isso vai dar:

2 x 2 . ϕ x y + x 2 + y 2 ϕ ' x y x y + 2 y ² . ϕ x y + x 2 + y 2 ϕ ' x y - x y y 2

= 2 x 2 . ϕ x y + x 2 + y 2 x y ϕ ' x y + 2 y 2 . ϕ x y - x 2 + y 2 x y ϕ ' x y

Opa! Vai dar pra cortar 2 desses troços estranhos!

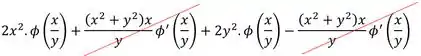
Então sobrou:

2 x 2 . ϕ x y + 2 y 2 . ϕ x y = 2 x 2 + 2 y 2 ϕ x y = 2 x 2 + y 2 ϕ x y = 2 u

Beleza! Conseguimos provar a equação! :D

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #5

George B. Thomas, Cálculo,Volume II,11º ed. São Paulo: Pearson Education do Brasil Ltda., 2009, pg. 317, exercício 22.

Calcule as derivadas parciais da função

f x , y = ∑ n = 0 ∞ x y n     ,     x y < 1

Passo 1

Essa é uma série geométrica

∑ n = 0 ∞ r n

Que converge quando r < 1 para

∑ n = 0 ∞ r n = f r = 1 1 - r

Sendo assim,

∑ n = 0 ∞ x y n = f x , y = 1 1 - x y

Pois   x y < 1

E, portanto, agora é só calcular as derivadas parciais normalmente, como estamos acostumados!

Passo 2

Calculando ∂ f ∂ x :

f x , y = 1 - x y - 1

∂ f ∂ x = - 1 - x y - 2 . ( - y )

∂ f ∂ x = y 1 - x y 2

Passo 3

Calculando ∂ f ∂ y :

f x , y = 1 - x y - 1

∂ f ∂ y = = - 1 - x y - 2 . ( - x )

∂ f ∂ y = x 1 - x y 2

Resposta

∂ f ∂ x = y 1 - x y 2

∂ f ∂ y = x 1 - x y 2

Exercícios de Livros Relacionados

Encontrar a inclinação da reta tangente à curva resultante da intersecção de z = f ( x , y ) com o plano x = x 0 no ponto P ( x 0 , y 0 ,z 0 ) .a) z = x 2 + y 2 - 1 ; P ( 1 ,- 1 ,1 )
Mostre que a função produção de Cobb-Douglas satisfaz P L , K 0 = C 1 K 0 L α resolvendo a equação diferencial d P d L = α P L
No estudo de penetração do congelamento descobriu-se que a temperatura T no instante t (medido em dias) a uma profundidade x (medida em pés) pode ser modelada pela função T ( x , t ) = T 0 + T 1 e - λ
80. A temperatura em um ponto x ,y de uma chapa de metal é dada por T x ,y = 60 / ( 1 + x 2 + y 2 ) , onde T é medido em ° C e x , y em metros. Determine a taxa de variação da temperatura no ponto 1 ,
Seja ϕ : R → R uma função diferenciável tal que ϕ ' 3 = 4 . Seja g x , y , z = ϕ x 2 + y 2 + z 2 . Calcule:a) ∂ g ∂ x 1,1 , 1 b) ∂ g ∂ y 1,1 , 1 c) ∂ g ∂ z 1,1 , 1