Coordenadas Cilíndricas - Cálculo
Produzido por Arthur Melo de AlmeidaTeoria
Fala aí, bem vindo ao RespondeAí e se você chegou nessa página é porque provavelmente ficou um pouco confuso com a explicação do seu professor sobre Coordenadas Cilíndricas, então vamos ver um exemplo para entendermos melhor do que se tratam as coordenadas cilíndricas!
As coordenadas cilíndricas são uma maneira de mudar estrategicamente a maneira de representar os pontos de uma curva no
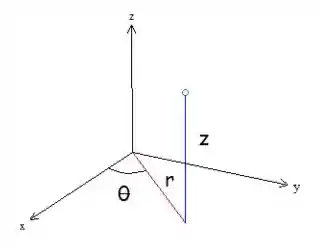
Para trabalhar com coordenadas cilíndricas, vamos usar as seguintes variáveis para definir um ponto:
que representa o raio do cilindro; que representa o ângulo de rotação em relação ao eixo no plano ; que é a altura em que o ponto está em relação ao plano
O interessante é que se olharmos "de cima" e ignorarmos a variável
Para fazer uma mudança de variável temos que saber calcular o Jacobiano da nossa transformação então primeiro precisamos nossas relações entre os diferentes sistemas de coordenadas:
Montando a matriz Jacobiana dessa mudança e calculando o determinante:
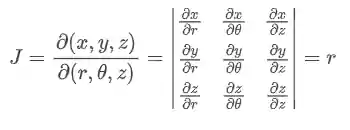
Com a informação do Jacobiano já conseguimos calcular qualquer integral tripla com o auxílio de coordenadas cilíndricas, dá uma olhada no exercício aqui em baixo:
Exercício
Nesse exercício do tópico de Mudança para Variáveis Cilíndricas nosso Expert resolve Passo a Passo para você entender bem esse conceito:
Determine o volume do sólido
Encontre todos os exercícios que você precisa para mandar bem em cálculo assinando o seu semestre com a gente!