Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Soma de Riemann

Ver Todos os Exercícios

Teoria

Opaa! Bora bater um papinho sobre a Soma de Riemann?!

O que são as Somas de Riemann?

A soma de Riemann é uma aproximação da área sob uma curva dividindo-a em infinitas formas simples, como retângulos. Assim:

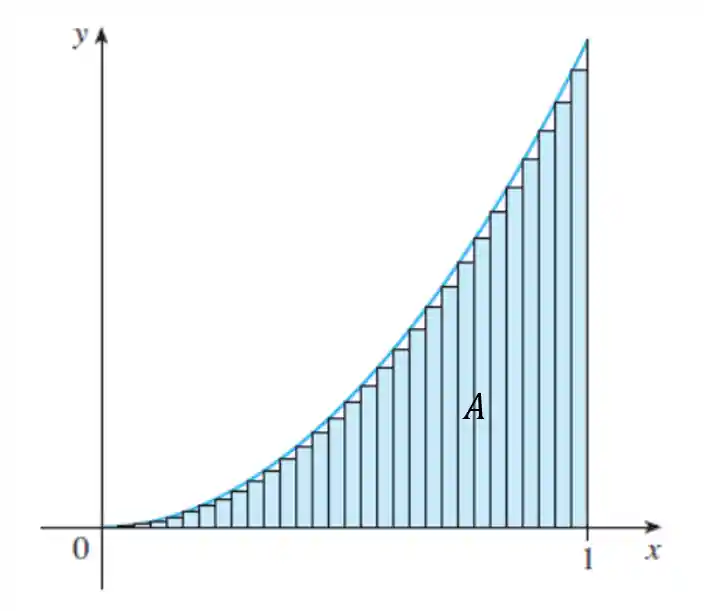
Gráfico com curva sombreada dividida em muitos retângulos.
Gráfico com curva sombreada dividida em muitos retângulos.

-Beleza, mas quando que eu vou usar isso?! 😖

Por exemplo, se você quiser calcular a área sob a curva da figura abaixo, poderíamos integrar usando a Antiderivação, afinal sabemos que , mas e quando não conhecemos a função ??

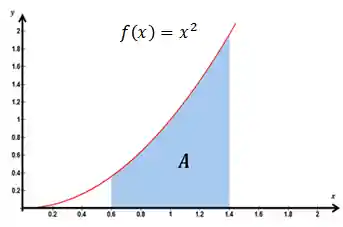
Gráfico de f(x)=x^2 com área A sombreada.
Gráfico de f(x)=x^2 com área A sombreada.

É ai que entra a Soma de Riemann!

A gente divide a área sob uma curva em infinito retângulos, porque é uma das formas mais simples pra a gente calcular! A fórmula da área do retângulo a gente tem na ponta da língua! 😉

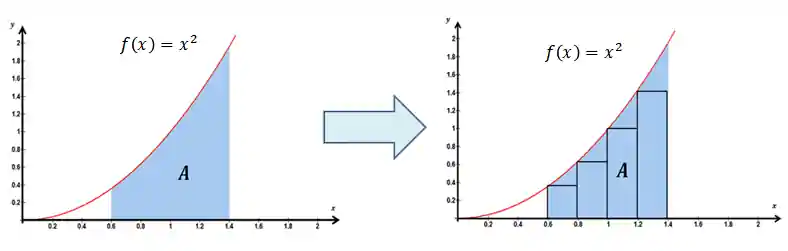
Dois gráficos de f(x)=x^2 com área A sombreada. No segundo a área A é dividida em retângulos.
Dois gráficos de f(x)=x^2 com área A sombreada. No segundo a área A é dividida em retângulos.

Agora, como achar o valor da área sob a curva a partir da Soma de Riemann?

Reparou que na figura acima “sobra” um espacinho entre a curva e os retângulos? Mas e se a gente desenhasse um monte de retângulos?

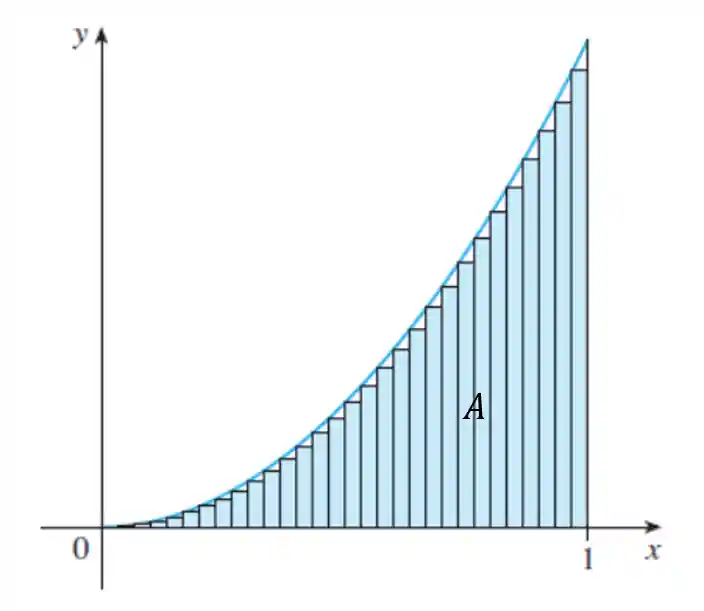
Gráfico com curva sombreada dividida em muitos retângulos.
Gráfico com curva sombreada dividida em muitos retângulos.

A aproximação da área fica mais fiel, certo?! Seguindo essa lógica, de uma forma geral podemos escrever:

Onde, é a soma de Riemann para esses infinitos retângulos. Ou seja, ao invés de integrarmos a função da curva, integramos os infinitos retângulos!

Como Calcular a Integral pela Soma de Riemann

Agora como podemos calcular o e assim obter a área aproximada?

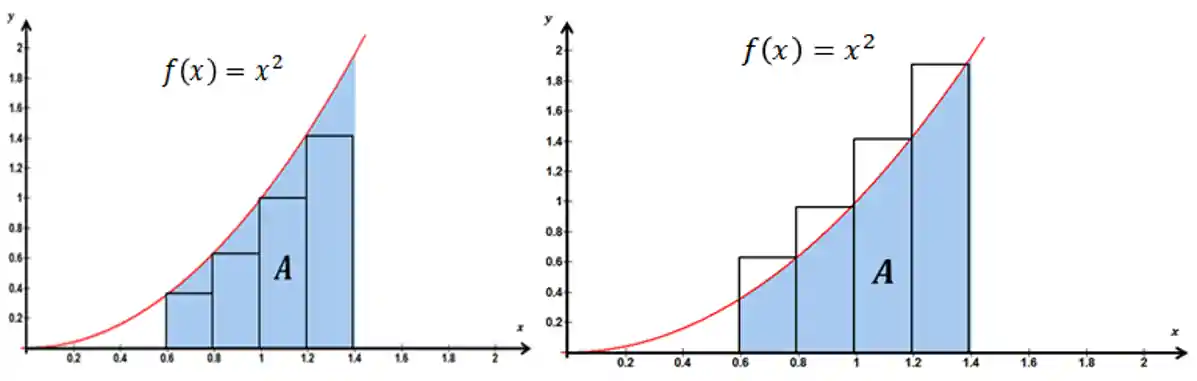
Gráficos com curvas divididas em retângulos. Soma de Riemann pela esquerda e pela direita
Gráficos com curvas divididas em retângulos. Soma de Riemann pela esquerda e pela direita

Repara que na primeira imagem acima desenhamos os retângulos com o lado esquerdo tocando a curva, nesse caso estamos subestimando a área sobre a curva, ou seja o valor aproximado que vamos achar vai ser menor que a área real.

Já na segunda imagem temos a situação contrária, fazendo a Soma de Riemann pela direita estamos superestimando a área, logo aproximação vai ser maior que a área real.

Nesse exemplo temos a função e a área sombreada esta entre e e vamos aprender a calcular a Soma de Riemann pela esquerda e pela direita.

Soma de Riemann pela Esquerda

Bora então achar o  pela Esquerda!?

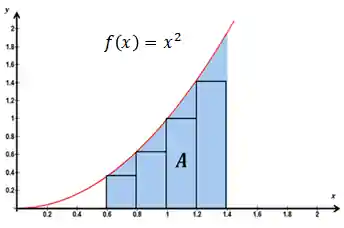
Soma de Riemann pela esquerda.
Soma de Riemann pela esquerda.

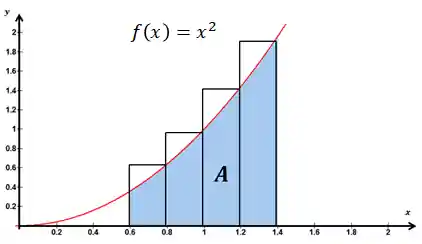
Na figura acima, dividimos a área em 4 retângulos que vão de até no eixo O tamanho da base de cada retângulo irá variar de acordo com quantidade de retângulos dentro desse espaço. Deste modo, vamos usar o para representar a base desses retângulos.

Para achar o podemos fazer o seguinte cálculo:

Conhecemos o e agora para calcular a área, precisamos achar a altura, certo?

Repara que altura do retângulo é limitada pela função naquele ponto. A altura do primeiro é , a altura do segundo é , a do terceiro é e do quarto é .

A figura abaixo deixa isso mais claro pra a gente:

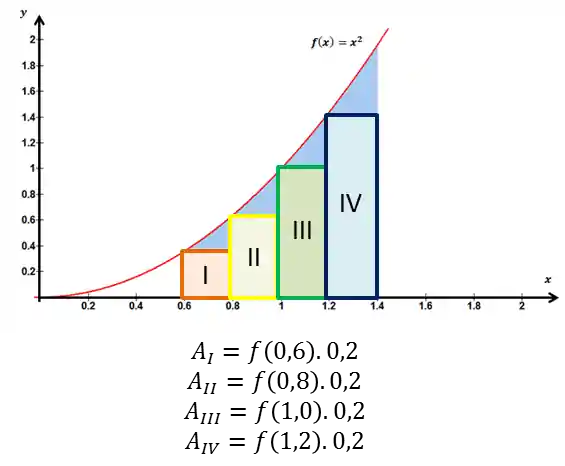
Área sobre a curva com retângulos divididos.
Área sobre a curva com retângulos divididos.

Então a nossa Soma de Riemann vai ser:

Substituindo:

Reparou que o apareceu em todos os termos? Beleza, segura essa informação!

Beleza, mas na prática queremos que o número de retângulos tenda ao infinito, então como faríamos essa conta para um número muito grande de retângulos?

Vamos então escrever todo esse cálculo para um caso geral:

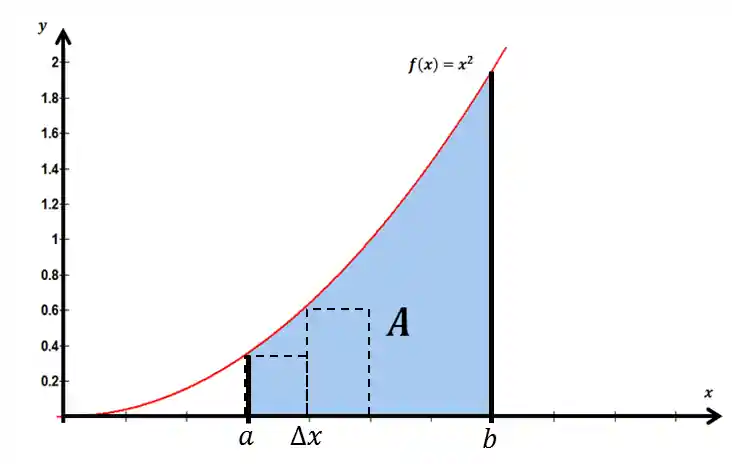
Área sobre a curva dividida em dois retângulos.
Área sobre a curva dividida em dois retângulos.

A fórmula da base ficará:

Onde é o limite de integração superior; e é o limite de integração inferior.

Já a altura será dada pela função no ponto . Então temos que a área do primeiro retângulo ficará:

Para o segundo retângulo:

para um terceiro retângulo:

Repara que temos um padrão, então de uma forma geral ficamos com:

Onde, pode ser dado por:

Iniciando com e indo até .

Agora que definimos quem é , podemos escrever a Soma de Riemann de uma forma mais agradável, usando o somatório!

Bem mais elegante, não?!

Soma de Riemann pela Direita

E como fica a Soma de Riemann pela direita?

Soma de Riemann pela direita.
Soma de Riemann pela direita.

O raciocínio é semelhante, mas o que vai mudar é o . Então a fórmula ficará:

Nesse caso o vai de até . Escrevendo o em forma de somatório, fica:

Qual das somas escolher?

Lembrando que aqui estamos falando de uma aproximação! Então precisamos prestar atenção em um detalhe importante! Uma das somas vai ter valor maior que a Integral tradicional, enquanto a outra vai ter valor menor. Para sabermos isso temos que prestar atenção se a função é crescente ou não.

Para uma função crescente:

Para uma função decrescente:

Exemplo: Como Integral pela Soma de Riemann

Achamos , mas lembra dessa fórmula lá do início do tópico?

Pois é, precisamos achar a Integral pela Soma de Riemann! Vamos então fazer um exemplo:

Dada o seguinte limite da soma de Riemann

Transforme na integral equivalente e calcule o valor da integral no intervalo .
A primeira coisa é entender bem essa soma de Riemann. Ele deu o intervalo de integração, logo ele deu o e o . Então podemos achar .

A soma de Riemann é:

Logo:

Substituindo os valores:

Aqui temos que procurar relações para achar o que falta para a integral, nesse exemplo é , mas podia ser o intervalo de integração também. Temos:

Podemos dizer que:

Substituindo:

E pronto, temos a nossa função :

A integral fica:

E é isso!

Passo a Passo para Achar a Integral pela Soma de Riemann:

Agora pra acabar, vamos para um passo a passo!

Passo 1 – Achar   em função de e ;

Passo 2 – Fazer  igual ao valor dentro do somatório, substituindo e ;

Passo 3 – Procurar relações para encontrar os valores que faltam para a integral

Passo 4 – Resolver a Integral

Prontinho! Agora podemos fazer os exercícios e achar a Integral pela Soma de Riemann!!!

Como Calcular a Integral pela Soma de Riemann

Exemplo: Como Integral pela Soma de Riemann

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Dada a função

f x = x 2           0 ≤ x ≤ 2

Determine a soma de Riemann pela esquerda e pela direita usando 8 retângulos, e coloque em ordem crescente o valor calculado e o valor real da área.

Passo 1

Vamos começar fazendo a soma de Riemann pela esquerda, lembra como é sua fórmula que vimos na teoria?

S n e s q u e r d a = f x 0 ∙ Δ x +   f x 1 ⋅ Δ x + f x 2 ⋅ Δ x + f x 3 ⋅ Δ x + … + f x n ⋅ Δ x

Onde

x i = a + i Δ x

Aqui começamos com i = 0 e terminando com i = n - 1 .

Com

Δ x = b - a n

Passo 2

Beleza, vamos identificar cada uma dessas paradas. O número de retângulos é o valor de n , então

n = 8

Além disso temos os valores do intervalo então

a = 0

b = 2

Beleza já temos praticamente tudo que precisamos para a soma

S 8 e s q u e r d a = f x 0 Δ x +   f x 1 Δ x + f x 2 Δ x + f x 3 Δ x + … + f x 7 ⋅ Δ x

O valor de Δ x vai ser

Δ x = 2 - 0 8 = 1 4

Agora vamos achar os valores de x i

x 0 = a = 0

x 1 = a + 1 . Δ x = 0 + 1 4 = 1 4

x 2 = a + 2 . Δ x = 0 + 2 . 1 4 = 2 4 = 1 2

x 3 = a + 3 . Δ x = 0 + 3 . 1 4 = 3 4

x 4 = a + 4 . Δ x = 0 + 4 . 1 4 = 1

x 5 = a + 5 . Δ x = 0 + 5 . 1 4 = 5 4

x 6 = a + 6 . Δ x = 0 + 6 . 1 4 = 6 4 = 3 2

x 7 = a + 7 . Δ x = 0 + 7 1 4 = 7 4

Passo 3

A soma vai ficar

S 8 e s q u e r d a = 0 2 . 1 4 + 1 4 2 . 1 4 + 1 2 2 . 1 4 + 3 4 2 . 1 4 + 1 2 . 1 4 + 5 4 2 . 1 4 + 3 2 2 . 1 4 + 7 4 2 . 1 4

S 8 e s q u e r d a = 0 + 1 64 + 1 16 + 9 64 + 1 4 + 25 64 + 9 16 + 49 64

S 8 e s q u e r d a = 1 + 4 + 9 + 16 + 25 + 36 + 49 64

S 8 e s q u e r d a = 140 64 = 35 16

Passo 4

Vamos agora para a soma pela direita

S n d i r e i t a =   f x 1 ⋅ Δ x + f x 2 ⋅ Δ x + f x 3 ⋅ Δ x + … + f x n ⋅ Δ x

Onde

x i = a + i Δ x

Aqui começamos com i = 1 e terminando em i = n .

Passo 5

No caso da soma pela direita vamos ter x i levemente diferentes, vamos recalcular para você ver.

x 1 = a + 1 . Δ x = 0 + 1 4 = 1 4

x 2 = a + 2 . Δ x = 0 + 2 . 1 4 = 2 4 = 1 2

x 3 = a + 3 . Δ x = 0 + 3 . 1 4 = 3 4

x 4 = a + 4 . Δ x = 0 + 4 . 1 4 = 1

x 5 = a + 5 . Δ x = 0 + 5 . 1 4 = 5 4

x 6 = a + 6 . Δ x = 0 + 6 . 1 4 = 6 4 = 3 2

x 7 = a + 7 . Δ x = 0 + 7 1 4 = 7 4

x 8 = a + 8 . Δ x = 0 + 8 1 4 = 8 4 = 2

Repara que o x 0 não entra nessa conta e o x 8 que não tinha agora apareceu, essa é a grande diferença.

O primeiro cara sai e acrescentamos um novo último.

Passo 6

A soma vai ficar

S 8 d i r e i t a = 1 4 2 . 1 4 + 1 2 2 . 1 4 + 3 4 2 . 1 4 + 1 2 . 1 4 + 5 4 2 . 1 4 + 3 2 2 . 1 4 + 7 4 2 . 1 4 + 2 2 . 1 4

S 8 d i r e i t a = 1 64 + 1 16 + 9 64 + 1 4 + 25 64 + 9 16 + 49 64 + 1

S 8 d i r e i t a = 1 + 4 + 9 + 16 + 25 + 36 + 49 + 64 64

S 8 d i r e i t a = 204 64 = 51 16

Passo 7

Ele quer agora comparar as duas contas que fizemos com o valor real da área, que seria a integral. Vamos chamar esse valor de A .

Como x 2 é crescente nesse intervalo vamos ter, como vimos na teoria, que

S 8 e s q u e r d a < A < S 8 d i r e i t a

Resposta

S 8 e s q u e r d a = 35 16

S 8 d i r e i t a = 51 16

S 8 e s q u e r d a < A < S 8 d i r e i t a

Exercício Resolvido #2

Elaboração Própria

Dada a função

f x = 1 x

Determine a soma de Riemann tanto pela esquerda quando pela direita no intervalo 1,5 .

Compare os dois valores encontrados.

Passo 1

Vamos começar fazendo a soma de Riemann pela esquerda, lembra como é sua fórmula que vimos na teoria?

S n e s q u e r d a = f x 0 ∙ Δ x +   f x 1 ⋅ Δ x + f x 2 ⋅ Δ x + f x 3 ⋅ Δ x + … + f x n - 1 ⋅ Δ x

Podemos ver essa soma também como

S n e s q u e r d a = ∑ i = 0 n - 1 f x i ∙ Δ x

Onde

x i = a + i Δ x

Aqui começamos com i = 0 e terminando com i = n - 1 .

Com

Δ x = b - a n

Beleza, vamos identificar cada uma dessas paradas. Aqui ele não deu o número de retângulos, então vamos deixar como n mesmo.

Além disso temos os valores do intervalo então

a = 1

b = 5

Beleza já temos praticamente tudo que precisamos para a soma

O valor de Δ x vai ser

Δ x = 5 - 1 n = 4 n

Agora vamos achar os valores de x i

x i = a + i Δ x

x i = 1 + i . 4 n

A soma vai ficar

S n e s q u e r d a = ∑ i = 0 n - 1 f 1 + i . 4 n ∙ 4 n

Que vai ser

S n e s q u e r d a = ∑ i = 0 n - 1 1 1 + i . 4 n ∙ 4 n

Dando uma arrumada vamos ter

S n e s q u e r d a = ∑ i = 0 n - 1 n n + 4 i ∙ 4 n

S n e s q u e r d a = ∑ i = 0 n - 1 4 n + 4 i

Passo 2

Vamos agora para a soma pela direita

S n d i r e i t a =   f x 1 ⋅ Δ x + f x 2 ⋅ Δ x + f x 3 ⋅ Δ x + … + f x n ⋅ Δ x

Podemos ver essa soma também como

S n d i r e i t a = ∑ i = 1 n f x i ∙ Δ x

Onde

x i = a + i Δ x

Aqui começamos com i = 1 e terminando em i = n .

O valor de x i não vai mudar, o que vai mudar é quais desses valores vamos pegar, nesse caso começando com x 1 e terminando com x n

O primeiro cara sai e acrescentamos um novo último.

A soma vai ficar

S n d i r e i t a = ∑ i = 1 n f 1 + i . 4 n ∙ 4 n

S n d i r e i t a = ∑ i = 1 n 1 1 + i . 4 n ∙ 4 n

Arrumando isso

S n d i r e i t a = ∑ i = 1 n 4 n + 4 i

Passo 3

Vamos agora compara os dois caras, vamos lembrar quem eles são

S n e s q u e r d a = ∑ i = 0 n - 1 4 n + 4 i

S n d i r e i t a = ∑ i = 1 n 4 n + 4 i

Repara que o termo geral é igual, mas um começa com i = 0 e termina em i = n - 1 e outro começa em i = 1 e termina em i = n

Vamos ver quem é maior que vem fazendo a subtração desses dois caras.

S n d i r e i t a - S n e s q u e r d a = ∑ i = 1 n 4 n + 4 i - ∑ i = 0 n - 1 4 n + 4 i

Bem, o termo geral é o mesmo, então para todos os valores de i = 1 até i = n - 1 o termo geral do primeiro somatório será igual ao do segundo, logo eles vão se anular. Sendo assim, só sobra o termo i = n do primeiro somatório e o termo i = 0 do segundo:

S n d i r e i t a - S n e s q u e r d a = 4 n + 4 n - 4 n + 4.0

S n d i r e i t a - S n e s q u e r d a = 4 5 n - 4 n

S n d i r e i t a - S n e s q u e r d a = 4 5 n - 20 5 n

S n d i r e i t a - S n e s q u e r d a = - 16 5 n

Isso nos diz que a soma pela esquerda é maior, o que faz todo sentido de acordo com o que já vimos na teoria, já que 1 x é uma função decrescente.

Resposta

S n e s q u e r d a = ∑ i = 0 n - 1 4 n + 4 i

S n d i r e i t a = ∑ i = 1 n 4 n + 4 i

S n e s q u e r d a - S n d i r e i t a = - 16 5 n

Exercício Resolvido #3

Elaboração Própria

Dada o seguinte limite da soma de Riemann

lim n → + ∞ ⁡ S n = lim n → + ∞ ⁡ ∑ i = 1 n n 4 i 5

Transforme na integral equivalente e calcule o valor da integral no intervalo 0,1 .

Passo 1

Temos que comparar aquela soma de Riemann com a fórmula da soma de Riemann para acharmos a , b e f x para podermos fazer a integral.

Ele deu no intervalo de integração, então temos

a = 0

b = 1

E

Δ x = 1 - 0 n = 1 n

Passo 2

Vamos agora comparar o termo geral daquele somatório com o termo geral da soma de Riemann

f a + i Δ x ∙ Δ x = n 4 i 5

Trocando os valores que temos

f 0 + i n ∙ 1 n = n 4 i 5

f i n = n 5 i 5

Vamos fazer

x = i n → i = x n

f x = n 5 x 5 n 5 = 1 x 5

Agora temos a nossa f x

Passo 3

Ufa, coisa a vera, mas achamos o valor da função, agora é só integrar e correr para o abraço

lim n → + ∞ ⁡ S n = lim n → + ∞ ⁡ ∑ i = 1 n i 4 n 5 = ∫ 0 1 1 x 5 d x

A integral vai ficar

∫ 0 1 1 x 5 d x = ∫ 0 1 x - 5 d x = - x - 4 4 x = 0 1 = - 1 4 - 0 = - 1 4

Resposta

- 1 4

Exercício Resolvido #4

Elaboração Própria

Dada o seguinte limite da soma de Riemann

lim n → + ∞ ⁡ S n = lim n → + ∞ ⁡ ∑ i = 0 n - 1 2 n 2 3 n + 2 i 3

Transforme na integral equivalente e calcule o valor da integral.

Passo 1

Vamos começar entendendo essa soma de Riemann aí

S n = ∑ i = 0 n - 1 2 n 2 3 n + 2 i 3

Como ela começa em i = 0 e termina em i = n - 1 ela é uma soma pela esquerda, a forma geral da soma pela esquerda é

S n e s q u e r d a = ∑ i = 0 n - 1 f x i ∙ Δ x

Então temos que comparar um termo dentro do somatório com o outro dentro do outro somatório.

f x i ∙ Δ x = 2 n 2 3 n + 2 i 3

Mas isso só atrapalhou sua vida né? E ainda por cima ele não deu o intervalo de integração, vamos chamar um de a e outro de b , assim escrevemos Δ x e x i em função desses dois carinhas

Δ x = b - a n

E

x i = a + i Δ x

x i = a + i b - a n = n a + i b - a n

Assim vamos ter

f n a + i b - a n ∙ b - a n = 2 n 2 3 n + 2 i 3

Eita confusinho de leve essa bagunça né? Vamos jogar aquele n do denominador para o outro lado multiplicando

f n a + i b - a n ∙ b - a = 2 n 3 3 n + 2 i 3

Dando uma arruma temos

f n a + i b - a n ∙ b - a = 2 n 3 3 n + 2 i 3

f n a + i b - a n ∙ b - a = 2 n 3 n + 2 i 3

Repara que temos um cara ao cubo levemente parecido com o cara dentro de f , se eu invertesse aquela fração dava igual, então vamos arrumar de novo, invertendo a fração e mudando o sinal do expoente

f n a + i b - a n ∙ b - a = 2 3 n + 2 i n - 3

Olha que beleza, se a função f x fosse x - 3 teriamos

n a + i b - a n = 3 n + 2 i n

E

b - a = 2

Vamos com calma agora, isso nos diz que

n a + i 2 n = 3 n + 2 i n

Comparando temos que a = 3 , assim

b - 3 = 2

b = 5

E achamos a , b e a função f x

a = 3

b = 5

f x = x - 3

DICA MAROTA:

Quando tivermos um cara na soma de Riemann com a potência do numerador sendo um a mais ou um a menos que a do denominador é interessante procurarmos f x como algumas funções tipo x n

Passo 2

A nossa integral vai ficar

lim n → + ∞ ⁡ S n = lim n → + ∞ ⁡ ∑ i = 0 n - 1 2 n 2 3 n + 2 i 3 = ∫ 3 5 x - 3 d x

Vamos ter

∫ 3 5 x - 3 d x = x - 2 - 2 x = 3 x = 5 = - 5 - 2 2 - - 3 - 2 2 = - 1 25.2 + 1 9 . 2 = 1 1 8 - 1 50 = 25 - 9 45 0 = 8 2 25

Resposta

8 2 25

Exercício Resolvido #5

Elaboração Própria

Dada a função

f x = 1 x           1 ≤ x ≤ e

Determine a soma de Riemann pela esquerda e pela direita usando 2 retângulos, e coloque em ordem crescente o valor calculado e o valor real da área.

Passo 1

Vamos começar fazendo a soma de Riemann pela esquerda, lembra como é sua fórmula que vimos na teoria?

S n e s q u e r d a = f x 0 ∙ Δ x +   f x 1 ⋅ Δ x + f x 2 ⋅ Δ x + f x 3 ⋅ Δ x + … + f x n ⋅ Δ x

Onde

x i = a + i Δ x

Aqui começamos com i = 0 e terminando com i = n - 1 .

Com

Δ x = b - a n

Passo 2

Beleza, vamos identificar cada uma dessas paradas. O número de retângulos é o valor de n , então

n = 2

Além disso temos os valores do intervalo então

a = 1

b = e

Beleza já temos praticamente tudo que precisamos para a soma

S 2 e s q u e r d a = f x 0 Δ x +   f x 1 Δ x

S 2 e s q u e r d a = Δ x f x 0 +   f x 1

O valor de Δ x vai ser

Δ x = e - 1 2

Agora vamos achar os valores de x i

x 0 = a = 1

x 1 = a + 1 . Δ x = 1 + e - 1 2 = e + 1 2

Passo 3

A soma vai ficar

S 2 e s q u e r d a = e - 1 2 1 1 + 2 e + 1

S 2 e s q u e r d a = e - 1 2 + e - 1 e + 1 = e - 1 e + 1 2 e + 1 + 2 e - 1 2 e + 1 = e 2 + 2 e - 3 2 e + 1  

S 2 e s q u e r d a = e - 1 e + 3 2 e + 1 ≅ 1,32

Passo 4

Vamos agora para a soma pela direita

S n d i r e i t a =   f x 1 ⋅ Δ x + f x 2 ⋅ Δ x + f x 3 ⋅ Δ x + … + f x n ⋅ Δ x

Onde

x i = a + i Δ x

Aqui começamos com i = 1 e terminando em i = n .

Passo 5

No caso da soma pela direita vamos ter x i levemente diferentes, vamos recalcular para você ver.

x 1 = a + 1 . Δ x = 1 + e - 1 2 = e + 1 2

x 2 = a + 2 . Δ x = 1 + 2 . e - 1 2 = e

Repara que o x 0 não entra nessa conta e o x 2 que não tinha agora apareceu, essa é a grande diferença.

O primeiro cara sai e acrescentamos um novo último.

Passo 6

A soma vai ficar

S 2 d i r e i t a = e - 1 2 2 e + 1 + 1 e = e - 1 2 2 e + 1 + 2 2 e = e - 1 1 e + 1 + 1 2 e

S 2 d i r e i t a = e - 1 2 e 2 e e + 1 + e + 1 2 e e + 1 = e - 1 3 e + 1 2 e e + 1

S 2 d i r e i t a = 3 e + 1 e - 1 2 e e + 1 ≅ 0,78

Passo 7

Ele quer agora comparar as duas contas que fizemos com o valor real da área, que seria a integral. Vamos chamar esse valor de A .

Como 1 x é decrescente nesse intervalo vamos ter, como vimos na teoria, que

S 2 e s q u e r d a > A > S 2 d i r e i t a

Se quiséssemos ainda fazer as contas:

A = ∫ 1 e 1 x d x = ln ⁡ x x = 1 x = e = ln ⁡ e - ln ⁡ 1 = 1 - 0 = 1

E, de fato:

S 2 e s q u e r d a > A > S 2 d i r e i t a

e - 1 e + 3 2 e + 1 > A > 3 e + 1 e - 1 2 e e + 1

1,32 > 1 > 0,78

Resposta

A = ∫ 1 e 1 x d x = 1

S 2 e s q u e r d a > A > S 2 d i r e i t a

e - 1 e + 3 2 e + 1 > A > 3 e + 1 e - 1 2 e e + 1

1,32 > 1 > 0,78

Exercícios de Livros Relacionados

Se A é a área sob a curva y = e x de 1 a 3 , use o Exercício 25 para encontrar um valor de n tal que R n - A0,0001 .
Com uma calculadora programável (ou um computador), é possível calcular as expressões para a soma das áreas de retângulos aproximantes, mesmo para valores grandes de n , usando l a ç o s ç . (Numa T I
Demonstre que: ∫ a b x d x = b 2 - a 2 2
Com uma calculadora programável ou computador (veja as instruções para o Exercício 9 da Seção 5.1), calcule as somas de Riemann esquerda e direita para a função f x = sen ⁡ ( x 2 ) no intervalo [ 0,1
Expresse a integral como um limite de somas. Depois, calcule, usando um sistema de computação algébrica para encontrar a soma e o limite.∫ 2 10 x 6 d x