Se , use um gráfico para conjecturar se é conservativo. Então, determine se sua conjectura estava correta.
Passo 1
Faala, galera, beleza?
Nessa questão precisamos fazer duas coisas.
A primeira é plotar o gráfico do campo vetorial
E a partir do desenho, supor se esse campo é ou não conservativo.
Vamos usar o Mathematica pra desenhar esse gráfico.
A segunda é confirmar se essa suposição estava certa ou não.
Bom, pra supor pelo desenho se um campo vetorial é conservativo, temos que lembrar que campos conservativos têm a seguinte característica:
Onde é uma curva fechada.
Então, vamos pegar uma curva fechada e olhar pros vetores que partem dos pontos dela:
- Caso todos estejam apontando na mesma direção da curva (ou todos na direção contrária), é provável que a os termos de , que somam na integral, não se cancelem e o campo não seja conservativo.
- Caso estejam apontando em direções diferente (alguns na mesma direção da curva, outros na contrária), é provável que os termos se cancelem, e o campo seja conservativo.
Agora, pra confirmar se o campo realmente é conservativo ou não, temos que:
Dado um campo
Ele é conservativo se:
Então na segunda parte do problema, vamos calcular as derivadas parciais e confirmar se elas são iguais.
Passo 2
Começamos plotando o gráfico de , usando o seguinte comando no Mathematica:

E ele retornou o seguinte:
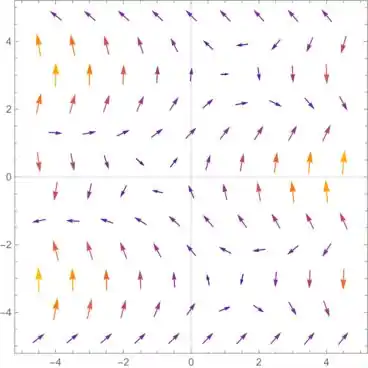
Vamos desenhar uma curva fechada nesse campo e analisar os vetores que partem dos pontos dela:
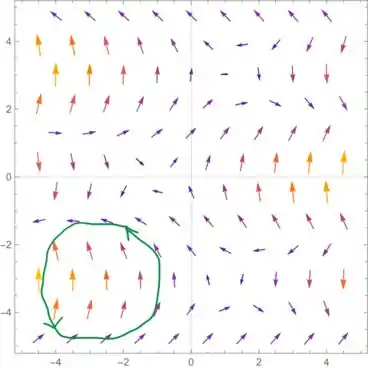
Percebe que temos vetores tanto acompanhando a direção da curva quanto vetores contrários a ela. Isso indica que provavelmente o campo é conservativo!
Passo 3
Para provar que a função é conservativa, temos que provar que
Onde
Calculando as derivadas parciais.
Primeiro de em função de , considerando constante:
Agora derivando em função de , com constante:
Então:
E confirmamos que o campo é realmente conservativo!
Resposta
é conservativo.