Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.7 - Ex. 37

37.Encontre o centroide do trapézio de vértices ( - a , 0 ) , ( a , 0 ) , ( - b , c ) e ( b , c ) .

Passo 1

Nessa questão, vamos começar desenhando esse triângulo, pois assim veremos qual fórmula do centroide usar.

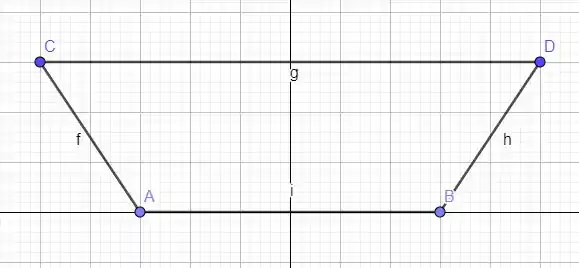
Vamos utilizar a fórmula abaixo dos centroides:

x - = 1 á r e a   d e   R ∫ a b 1 2 w 2 ( y ) - v 2 ( y ) d y

y - = 1 á r e a   d e   R ∫ a b y w y - v y d y

Passo 2

Vamos começar descobrindo as funções que delimitam o triângulo!

A reta A C vai do ponto ( 0 , - a ) até ( - b , c ) . Então a função da reta A B é:

y = c - a b x - a

Isolando o x , temos:

x = b ( y + a ) c - a

v y = b ( y + a ) c - a

E a reta B D ( 0 , a ) até ( b , c ) . Então a função da reta A B é:

y = c - a b x + a

Isolando o x , temos:

x = b ( y - a ) c - a

w y = b ( y - a ) c - a

Vamos calcular a área desse triângulo pela integral:

Á r e a = ∫ 0 c b ( y - a ) c - a - b ( y + a ) c - a d y = b c - a ∫ 0 c y - a d y - b c - a ∫ 0 c y + a d y

Paramos nessa integral:

Á r e a = b c - a ∫ 0 c y - a d y - b c - a ∫ 0 c y + a d y

Fazendo individualmente cada integral:

∫ 0 c y - a d y = y 2 2 c 0 - a y c 0 = c 2 2 - a c

∫ 0 c y + a d y = y 2 2 c 0 + a y c 0 = c 2 2 + a c

Á r e a = b c - a × c 2 2 - a c -

Voltando para a expressão da área:

Á r e a = b c - b a 2 - b c + b a 2 + 2 a b = - a b + 2 a b = a b

Passo 3

Vamos agora fazer o centroide em x .

x - = 1 a b ∫ 0 b x f x - g ( x ) d x = 1 a b ∫ 0 b x c - a b x + a - c + a b x - a d x = 1 a b ∫ 0 b c - a b x 2 - c + a b x 2 + 2 a x d x

Paramos nessa integral aqui:

x - = 1 a b ∫ 0 b c - a b x 2 - c + a b x 2 + 2 a x d x

= 1 a b ∫ 0 b c - a b x 2 d x - 1 a b ∫ 0 b c + a b x 2 d x + 1 a b ∫ 0 b 2 a x d x

Fazendo individualmente cada integral:

∫ 0 b c - a b x 2 d x = c - a b ∫ 0 b x 2 d x = c - a b × x 3 3 b 0 = c - a b × b 3 3 = b 2 c - b 2 a 3

∫ 0 b c + a b x 2 d x = c + a b ∫ 0 b x 2 d x = c + a b × x 3 3 b 0 = c + a b × b 3 3 = b 2 c + b 2 a 3

∫ 0 b 2 a x d x = 2 a ∫ 0 b d x = 2 a x 2 2 b 0 = a b 2

Voltando para a integral do centroide.

x - = 1 a b b 2 c - b 2 a 3 - 1 a b b 2 c + b 2 a 3 + 1 a b   a b 2 = b c - b a 3 a - b c + b a 3 a + b = - 2 b a 3 a + b = - 2 b 3 + b = b 3

E vamos fazer agora o centroide em y .

y - = 1 a b ∫ 0 b 1 2 c - a b x + a 2 - c + a b x - a 2 d x =

= 1 a b ∫ 0 b 1 2 c - a 2 b 2 x 2 + 2 a c - a 2 b x + a 2 - c + a 2 b 2 x 2 + 2 a c + a 2 b x - a 2 d x =

= 1 2 a b ∫ 0 b c - a 2 b 2 x 2 - c + a 2 b 2 x 2 + 4 a c b x d x =

= 1 2 a b ∫ 0 b c - a 2 b 2 x 2 d x - 1 2 a b ∫ 0 b c + a 2 b 2 x 2 d x + 1 2 a b ∫ 0 b 4 a c b x d x

Vamos fazer essas integrais individualmente:

∫ 0 b c - a 2 b 2 x 2 d x = c - a 2 b 2 ∫ 0 b x 2 d x = c 2 - 2 a c + a 2 b 2 x 3 3 b 0 = c 2 - 2 a c + a 2 b 2 b 3 3 = b c 2 - 2 a b c + a 2 b 3

∫ 0 b c + a 2 b 2 x 2 d x = c + a 2 b 2 ∫ 0 b x 2 d x = c 2 + 2 a c + a 2 b 2 x 3 3 b 0 = c 2 + 2 a c + a 2 b 2 b 3 3 = b c 2 + 2 a b c + a 2 b 3

∫ 0 b 4 a c b x d x = 4 a c b ∫ 0 b x d x = 4 a c b x 2 2 b 0 = 4 a b c 2 = 2 a b c

Voltando para a integral, temos:

y - = 1 2 a b × b c 2 - 2 a b c + a 2 b 3 - 1 2 a b × b c 2 + 2 a b c + a 2 b 3 + 1 2 a b × 2 a b c = c 2 - 2 a c + a 2 6 a - c 2 + 2 a c + a 2 6 a + c = - 4 a c 6 a + c = 2 a c 6 a = c 3

Então o centroide é:

b 3 , c 3

E o encontro das medianas também é:

b 3 , c 3

Então o centroide é ponto de encontro das medianas.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A velocidade de um carro foi lida de seu velocímetro em intervalos de 10 segundos e registrada na tabela. Use a Regra do Ponto Médio para estimar a ditância percorrida pelo carro.
A seguir, está ilustrada a potência consumida na cidade de Ontário, Canadá, em 9 de dezembro de 2004 (P é medida em megawatts; t é medido em horas a partir da meia-noite). Usando o fato de que a potên
Repita o Exercício 47 para a curva y = x 2 + 1 - 1 - x 4 .
Use a Parte 2 do Teorema Fundamental do Cálculo para calcular a integral, ou explique por que ela não existe. ∫ - 2 3 x - 5d x
Use a Parte 2 do Teorema Fundamental do Cálculo para calcular a integral, ou explique por que ela não existe. ∫ - 5 5 2 x 3d x