Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 6.1 - Ex. 51
51. No Exemplo 5, modelamos a curva patogênese do sarampo por uma função . Um paciente infectado pelo vírus tem uma curva patogênese que pode ser modelado por exemplo, por .
- Se for necessário o mesmo patamar de concentração do vírus que no Exemplo 5 para que o contagio comece, em que dia isso ocorre?
- Seja o ponto do gráfico de onde o contagio começa. Foi mostrado que o contagio acaba em um ponto do gráfico de tal que a reta por tem a mesma inclinação que a reta por no Exemplo 5(b). Em que dia o contagio acaba?
- Calcule o nível de contagio desse paciente.
Passo 1
Falaaa aí galerinha bonita! Tudo joinha?
Show de bolinhas então, no Exemplo 5, a função é dada por:
E como aqui queremos uma função tal que , então:
Belezinha, agora que já temos a função podemos ir pra letra (a).
Passo 2
Saca só, o enunciado diz pra gente que o contagio começa com o mesmo patamar de concentração, se a gente for lá no Exemplo 5, vamos ver que esse patamar acontece quando a concentração chega a 1210 ml, portanto, no nosso caso a concentração vai acontecer quando:
E como a gente é malandro, sabemos que a curva de contagio está crescendo nesse intervalo, por isso podemos assumir que quando a concentração cresce, o tempo cresce também, dessa forma não precisamos encontrar o valor exato de , apenas o dia em que isso ocorre, por exemplo, no dia 11, temos:
E para o dia 12, temos:
Logo:
Portanto, como já passamos do dia 11, quer dizer que o contágio começa no décimo segundo dia da infecção. Usando a alguma ferramenta de calculadora gráfica com , podemos conferir o resultado
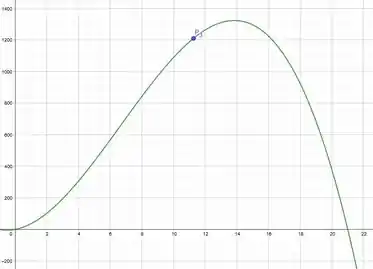
Encontramos .
Passo 3
Belezoca então amores, na letra (b), ele diz que a reta que passa por tem a mesma inclinação da reta que passa por do exemplo 5. E voltando no exemplo 5, vemos que essa inclinação, é dada por . Logo, essa reta no ponto é dada por:
E a malandragem aqui, é que essa reta cruza nossa curva 2 vezes, uma no ponto que já conhecemos, e outra no ponto , que estamos afim de encontrar. Portanto, plotando essa reta na nossa ferramenta gráfica, obtemos o seguinte:
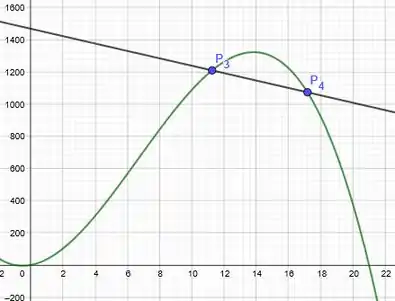
Onde é dada como , logo , ou seja, o contagio termina no décimo oitavo dia.
Passo 4
E por fim, na letra (c), o nível de contagio é dado pela área entre a curva de contagio e a reta :
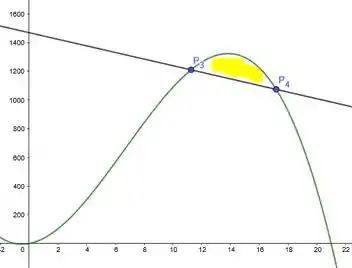
Ou seja:
Portanto o nível de contagio desse paciente é
Resposta
- , décimo segundo dia
- , décimo oitavo dia