Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 9.Revisão - Ex. 99
Ache a área da região limitada pelo laço da curva .
Passo 1
A questão pede para acharmos a área de um laço da curva . Ao plotarmos essa curva, obtemos
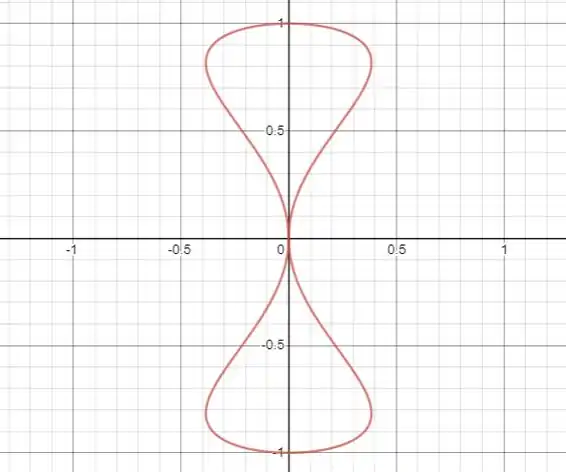
Como queremos a área de apenas um laço, estamos interessados na região com (acima do eixo ).
Se tentarmos isolar como função de , não vamos conseguir, mas é possível isolar como função de . Assim, esse é um problema que só pode ser resolvido se integrarmos na variável .
Isolando como função de , temos que
A área de um laço será o dobro da área da região no primeiro quadrante ), de modo que podemos escrever:
Passo 2
Para efetuarmos essa integral, vamos precisar da substituição trigonométrica . Assim,
Além disso, e, quando e para :
Usando a fórmula do arco duplo:
Assim,
Passo 3
Agora, fazendo , temos que :
Note que os limites de integração também devem ser alterados!
Para integrar , lembre-se que
Portanto,
Como , temos que